马拉车

POJ 3974：https://vjudge.net/problem/POJ-3974

拉车是用来处理回文问题的利器！既可以单独食用，又可以配合其他算法，如回文自动机，KMP，后缀数组来一起处理问题。

马拉车实质上是一个DP的过程。它利用了之前步骤的信息。

我们知道，回文串有奇数回文串 如aba，偶数回文串，如abba。

如果分开讨论那将是一件极其令人头痛的事情，故我们用特殊的手法来把所有回文串变成奇回文串。
这就是马拉车的初始化，

首先在字符串头加一个特殊字符，然后再在每个字符前加一个不同于首字符的特殊字符。

 

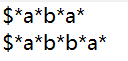
 然后在进行处理，我们可以找一个对称中心然后向左右拓展来找到回文串长度。

manacher算法利用DP的思想简化了这一过程。

首先，定义变量：

Mx表示当前求得最长回文右边界，Mid为该回文串的中点（保证奇数）
Lent[i]表示以i为中心的回文半径。比如单个字符a，它的回文半径就是1.
Lent[i]-1是整个回文串的长度（因为半径是在预处理下求得的半径）
算法过程：
For修改后字符串的每一位，设为i。
①：初始化lent[i]
②：判断i+lent[i]和i-lent[i]是否相等，如果相等就拓展
③：更新mx和mid

 Len数组的初始化就是利用的DP的思想。

 

 

在初始化的时候讨论了一下如果i<mx；我们就可以利用回文串的对称性，通过2*mid-i的位置的状态来初始化i处的状态。

lent[i]=min(lent[2*mid-i],mx-i);

通过对称状态和mx-i比较是因为mx之后的部分我们还没有扫描，超出了对称的范围。

最后看一下这个题目的代码。

#include<stdio.h>
#include<string.h>
int maxt=0,lent[2000004],mx,mid,p=0;
char s[1000002],tem[2000004];
void insert(char* st)
{
 int st_l=strlen(st);
 tem[0]='$';
 tem[1]='*';
 for(int i=1;i<=st_l;i++)
 {
  tem[2*i]=st[i-1];
  tem[2*i+1]='*';
 }
 tem[2*st_l+2]='\0';
}
int max(int a,int b)
{
 return a>b?a:b;
}
int min(int a,int b)
{
 return a>b?b:a;
}
int main()
{
 while(1)
 { p++;maxt=0;
  scanf("%s",s);
  if(!strcmp(s,"END")) break;
  insert(s);
  mx=0;mid=0;
  for(int i=1;tem[i];i++)
  {
   if(i<mx)
   {
    lent[i]=min(lent[2*mid-i],mx-i);
   }
   else lent[i]=1;
   while(tem[i+lent[i]]==tem[i-lent[i]]) lent[i]++;
   if(lent[i]+i>mx)
   {
    mx=lent[i]+i;mid=i;
   }
   maxt=max(maxt,lent[i]-1);
  }
  printf("Case %d: %d\n",p,maxt);
 }
 return 0;
}