机器学习公开课笔记第八周之异常检测
一,异常检测定义
异常检测就是训练一批正常的训练数据集,训练之后判定另一个数据\(X_{test}\)集中哪些数据是正常的
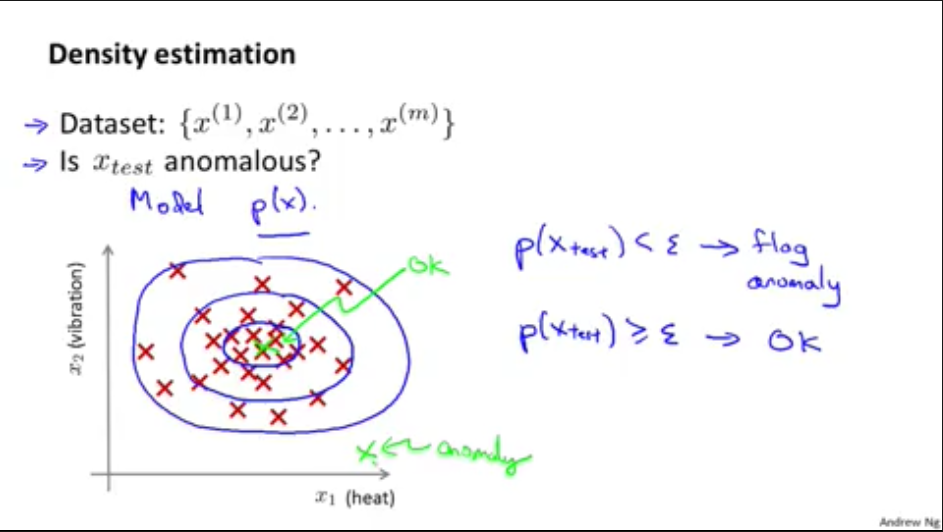
以下是异常检测的两个例子,分别是信用卡诈骗和数据中心电脑监测
1,提炼数据的特征\(X^{(i)}\)
2,从数据中训练出概率公式\(p(x)\)
3,用测试数据\(X_{test}\)计算\(p(x) < \epsilon \)

二,如何训练概率模型-高斯(正态)分布
1,高斯分布定义
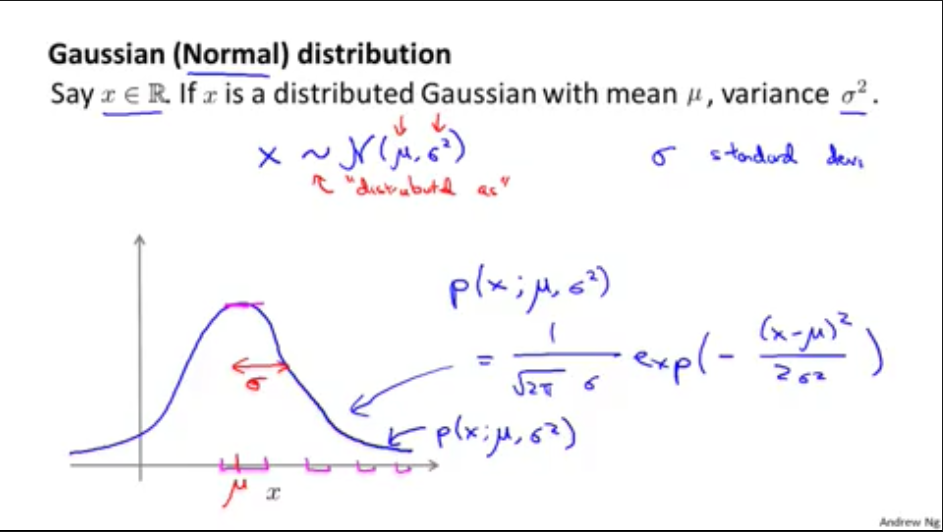
当\(x \in \mathbb{R} \),且属于平均值\(\mu\)和方差\(\sigma^{2}\)的高斯分布,即\(x \sim N(\mu, \sigma^{2})\),那么概率公式
\(p(x;\mu,\sigma^{2}) = \frac{1}{\sqrt{2\pi} \sigma} exp(-\frac{(x - \mu) ^ {2}}{2\sigma^{2}}) \)
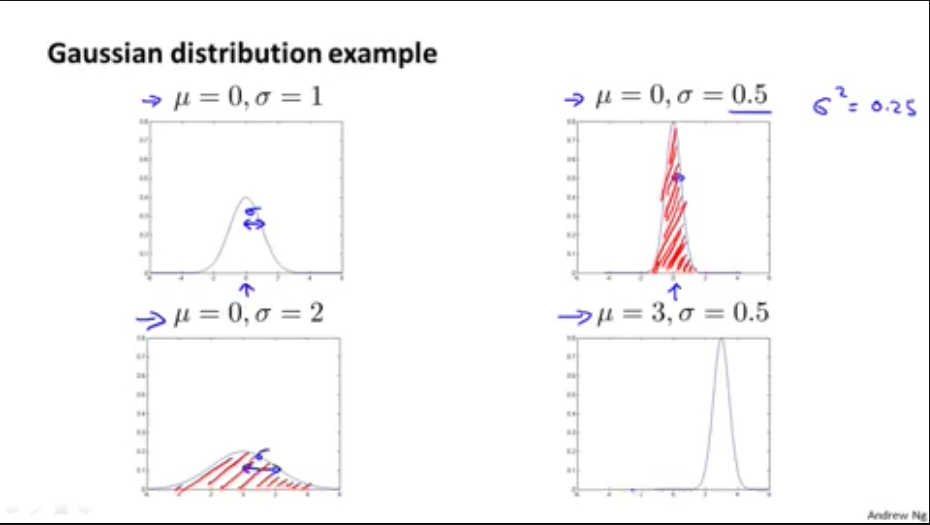
2,高斯分布例子
\(\mu\)并不影响高斯函数的形状,影响的是高斯函数的位置
因为高斯函数的面积等于1,所以随着\(\sigma\)变小,最大值变小,函数宽度变窄,也可从公式得出
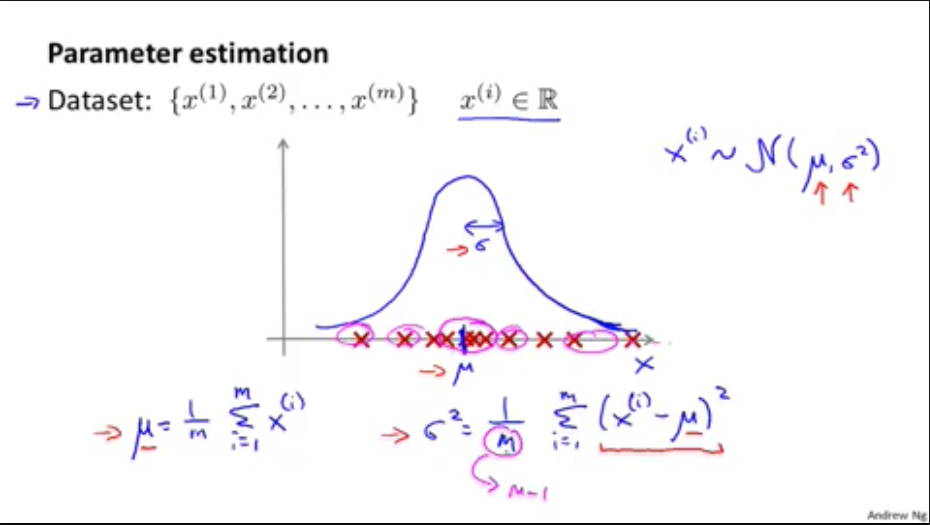
2,如何计算\(\mu\)和\(\sigma\)
如果数据集属于高斯分布,即\(x \sim N(\mu, \sigma^{2})\)
\(\mu =\frac{1}{m} \sum_{i = 1}^{m} x^{(i)}\)
\(\sigma^2 =\frac{1}{m} \sum_{i = 1}^{m} (x^{(i)} - \mu)^{2}\)
三,异常检测算法(高斯分布)
1,选择训练数据中相互独立的n个特征\(x_i\)
2,计算出n个独立特征的高斯分布的\(\mu_1,.....,\mu_n,\sigma_1^2,....\sigma_n^2\)
3,给定新数据,计算出\(p(x) = \prod_{j=1}^n p(x_j;\mu_j,\sigma_j^2) = \prod_{j=1}^n \frac{1}{\sqrt{2\pi} \sigma_j} exp(-\frac{(x_j - \mu_j) ^ {2}}{2\sigma_j^{2}})\)
4,判定数据是否异常取决于\(p(x) < \epsilon\)

例子
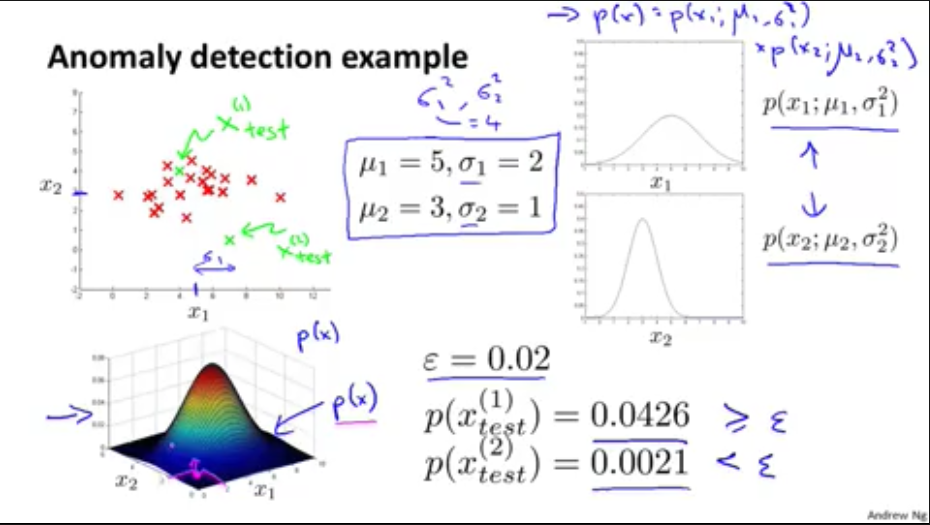
四,如何评估异常检测算法的优劣
评价算法优劣最好的方法就是量化优劣,让每个算法都返回一个数值,根据这个数值来比较优劣

1,把数据集按一定比例(6:2:2)分成训练集,交叉验证集,测试集
2,用测试集训练高斯分布模型
3,用交叉验证集的评估函数(如召回率,查准率和F1)选择\(\epsilon\)和有用特征
4,用测试集评估算法(如召回率,查准率和F1)

五,异常检测VS逻辑回归
异常检测也可以用于监督学习(有标签的数据),和逻辑回归的用法就相同,逻辑回归和异常检测的应用场景区别在与不同标签数据的比例
如果正标签比起负标签非常少(Skewed Data),那么选择异常检测,如果正标签比起负标签一样对,选择逻辑回归

异常检测和逻辑回归常用应用场景对比

当然应用场景也不是固定不变,最根本还是取决于数据比例
六,异常检测的特征选取
1,特征转化
因为是假设每个特征都符合高斯分布,那如果特征不符合高斯分步,可以对该特征进行转化,比如去该特征对数/(log(x) (x>0)/)

2,误差分析
和逻辑回归的异常检测一样,找出那些异常数据,看看这些数据有没有什么规律,根据这些规律创建新的特征
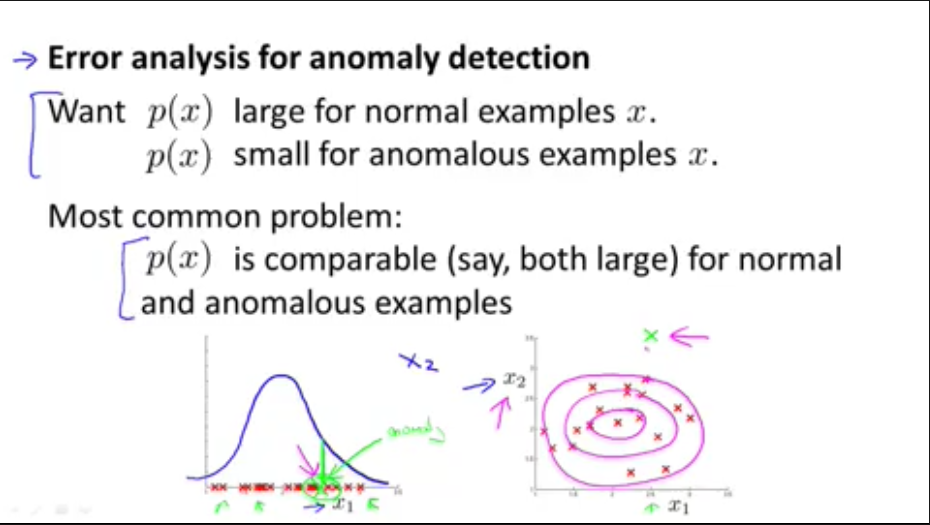
检测数据中心电脑误差分析的例子

七,多元高斯分布
1,多元高斯分布的由来
普通的高斯分布的前提的特征与特征之间是独立的,没有关系,但如果特征与特征之间有关系,比如线性相关,普通的高斯分布的模型就不适合,需要多元高斯分布模型
但也可以通过增加新特征来表示特征之间关系来解决

2,多元高斯分布定义

2,多元高斯分布例子
如果\(\Sigma\)只有对角线上大于0,和普通的高斯分布效果一样

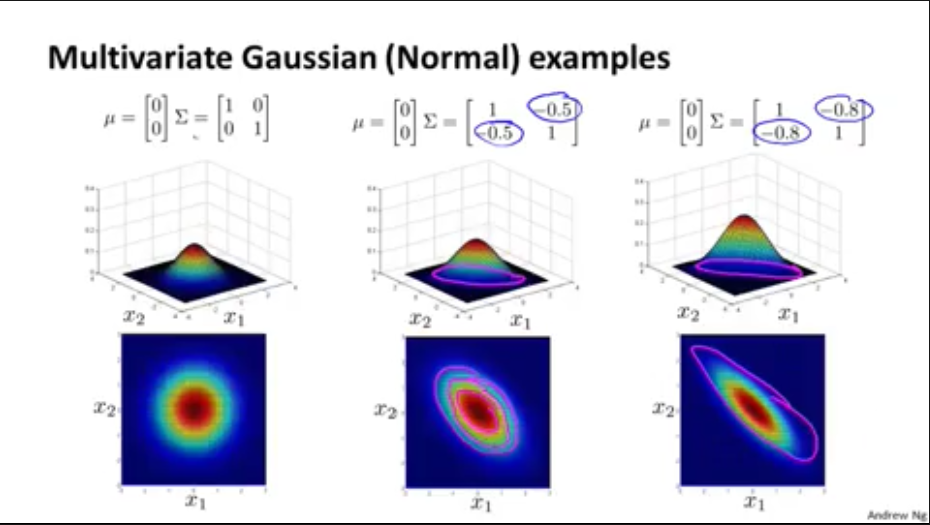
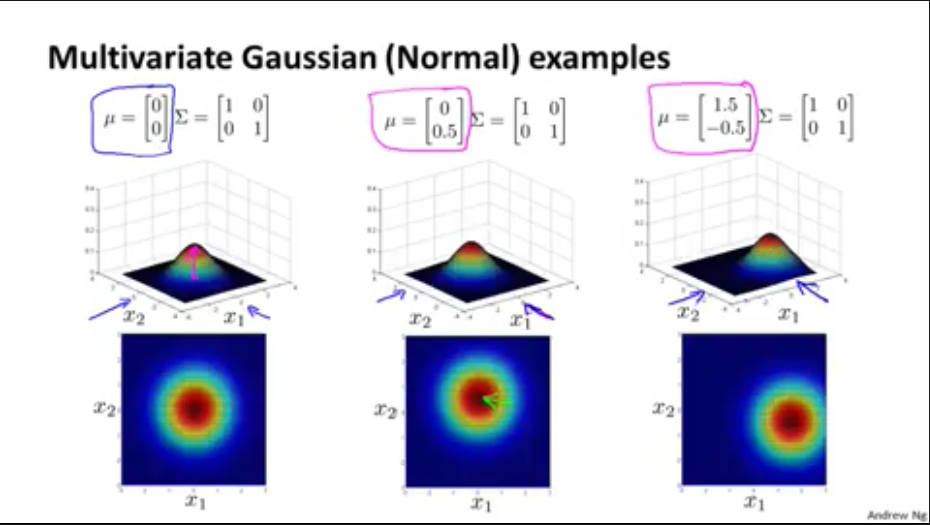
3,多元高斯分布算法
\(p(x;\mu,\Sigma) = \frac{1}{(2\pi)^{\frac{n}{2}}|\Sigma|^{\frac{1}{2}}} exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu))\)
\(\mu =\frac{1}{m} \sum_{i = 1}^{m} x^{(i)}\)
\(\Sigma = \frac{1}{m}\sum_{i=1}^{m}(x^{(i)}-\mu)(x^{(i)}-\mu)^T\)

原始高斯分布是多元高斯分布一种特例,当\(\Sigma\)矩阵对角上都是\(\sigma_i^2\),对角线外全0

4,多元高斯分布和原始高斯分布
1),多元高斯分布计算太慢,计算\(Sigma^{-1}\)需要\(O(n^3)\),当n>=10000时只能选择原始高斯分布
2),多元高斯分布可以自动关联特征之间的关系,原始高斯分布需要需要观察数据规律并手动添加特征来表示特征关系
3),多元高斯分布必须保证\(Sigma\)可逆,即m>n且没有冗余特征(数据矩阵的秩等于m)




