机器学习公开课笔记第六周,支持向量机
一,支持向量机(SVM)定义
支持向量机(SVM)和逻辑回归类似,也是二元分类,但是约束条件不同,它的目标是寻找一个超平面分割数据,这个超平面一侧是分类为-1的数据,一侧是是分类是1的数据
这样的超平面有很多,支持向量机还有一个约束条件是使两侧数据到这个超平面的距离最小值最大,所以支持向量机也叫大间距分类(Large Margin Classfication)
为了使超平面和数据有间距,分类为1的\(\theta^{T}x^{(i)} \geq 1\), 分类为0的\(\theta^{T}x^{(i)} \leq -1\)
所以代价函数就变为,\( min_{(\theta)} \frac{1}{m}\left[ \sum_{i=1}^{m} y^{(i)}cost_{1}{(\theta^{T}x^{(i)})} + (1 - y^{(i)})cost_{0}{(\theta^{T}x^{(i)})} \right] + \frac{\lambda}{2m}\sum_{j=1}^{n} {\theta_{j}}^{2}\)
\(cost_{1}{(\theta^{T}x^{(i)})}\)和\(cost_{0}{(\theta^{T}x^{(i)})}\)如下图所示
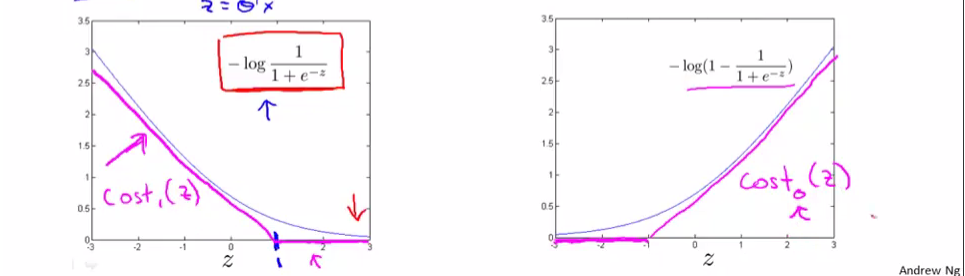
二,理解支持向量机
1,向量的内积
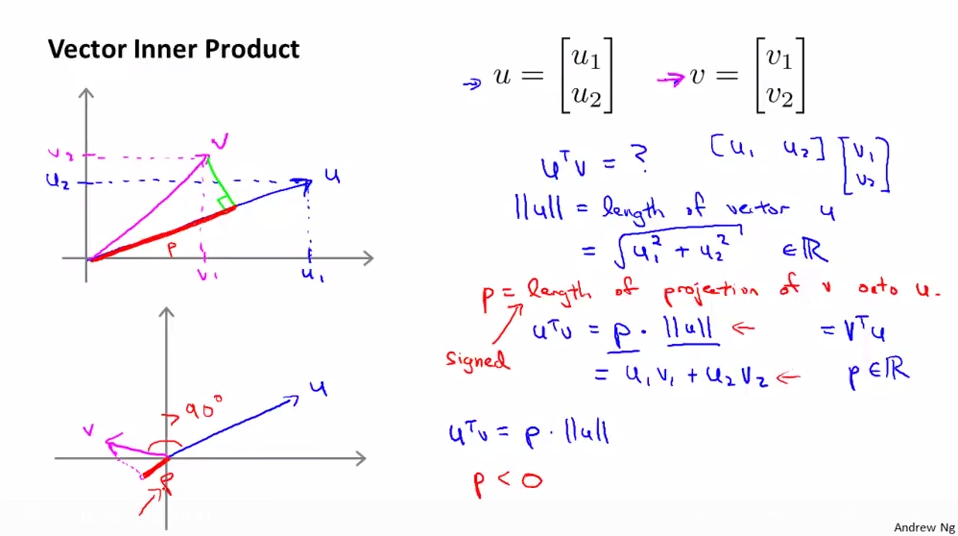
向量内积可以理解为一个向量到另一个向量的投影乘以另一个向量的膜
\(u^{T}v = p \cdot ||u|| = u_{1}v_{1} + u_{2}v_{2}\)
p是u到v的投影(有正负),\(||u|| = \sqrt{{u_{1}}^{2} + {u_{2}}^{2}}\)
2,SVM决策边界(超平面)
为了使超平面和数据有间距,分类为1的\(\theta^{T}x^{(i)} \geq 1\), 分类为0的\(\theta^{T}x^{(i)} \leq -1\),而不是以像逻辑回归一样以0为界限
超平面是由\(\theta\)决定,以两个特征的数据为例,先假设\(\theta_{0} = 0\)
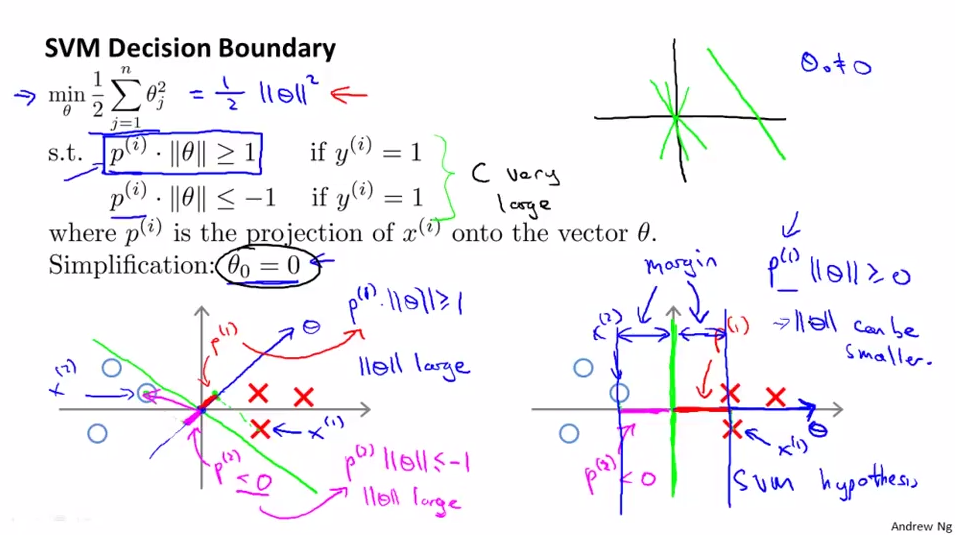
绿线表示决策边界(超平面),蓝线表示决策边界(超平面)的法向量\(\theta\),由图易得,数据\(X^{(i)}\)到\(\theta\)的投影\(p^{(i)}\)就是到决策边界(超平面)的距离,
因为约束条件是分类为1的\(\theta^{T}x^{(i)} \geq 1\), 分类为0的\(\theta^{T}x^{(i)} \leq -1\)
即\(p^{(i)} \cdot ||\theta|| \geq 1( if\ y^{(i)} = 1)\)
\(p^{(i)} \cdot ||\theta|| \leq 1 (if\ y^{(i)} = -1)\)
可以合并 \(y \cdot p^{(i)} \cdot ||\theta|| \geq 1\)
因为约束条件总能满足,所以只要\(||\theta||\)越小,投影\(p^{(i)}\)就越大,间距就越大,就越符合我们SVM的要求
又因为\( \frac{1}{2}\sum_{j=1}^{n} {\theta_{j}}^{2} = \frac{1}{2}||\theta||^{2}\),m是常数,并不影响求\(\theta\)的最小值,用C取代\(\lambda\), \(C= \frac{1}{\lambda}\)
\( min_{(\theta)} C\left[ \sum_{i=1}^{m} y^{(i)}cost_{1}{(\theta^{T}x^{(i)})} + (1 - y^{(i)})cost_{0}{(\theta^{T}x^{(i)})} \right] + \sum_{j=1}^{n} {\theta_{j}}^{2}\)
我们一般设C很大,为了使\(\left[ \sum_{i=1}^{m} y^{(i)}cost_{1}{(\theta^{T}x^{(i)})} + (1 - y^{(i)})cost_{0}{(\theta^{T}x^{(i)})} \right]\)尽量小,尽量满足约束条件,线性可分
3,内核(Kernel)
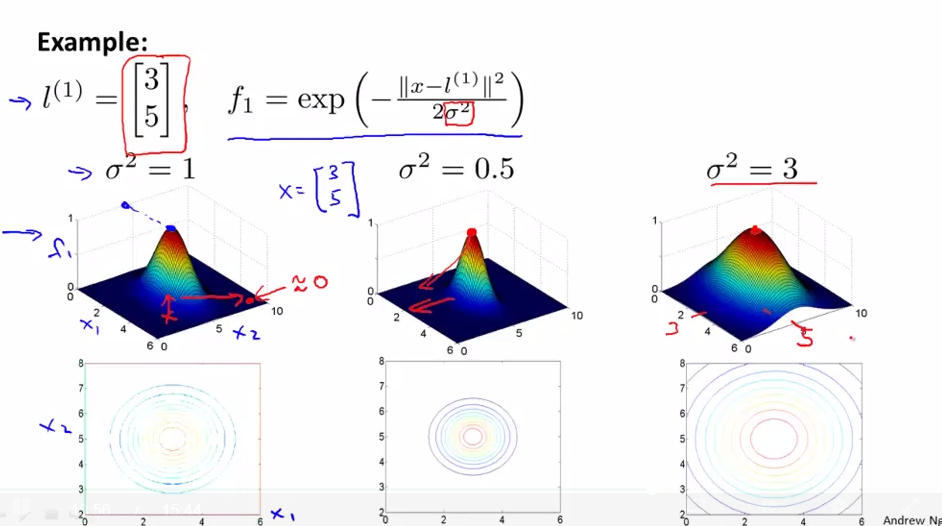
可以通过内核构造非线性决策边界函数,选定几个标记点\(l^{(i)}\),把每个数据与这些标记点的远近作为新特征,高斯内核的构造方式如下

高斯内核的方差变化示意图
一个非线性例子
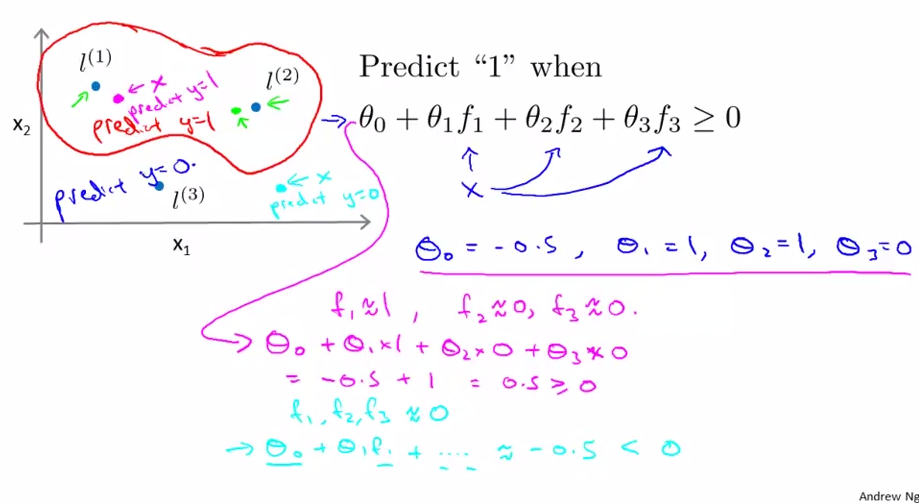
选取每个训练数据为标记点

使用高斯内核的SVM

C和\(\sigma \)和SVM模型的影响

尽管我们可以使用库来实现SVM,但是我们还是需要自己选择常数C和内核(Kernel)
我们还可使用线性内核(不使用内核,直接用\(\theta^{T}x \geq 0\))

在调用高斯内核产生新的特征f时,必须使用特征缩放(Feature Scaling),否则权值大的某个特征直接决定改新数据

我们还可使用其它内核,但必须满足塞尔定理(Mercer's Theorem),塞尔定理保证SVM的优化正确运行,收敛于最小值
可以使用多现实内核

多元分类的处理和逻辑回归处理类似,可以看成K个二元分类

逻辑回归还是SVM

使用逻辑回归还是SVM的一种方法是取决于特征数量n和训练数据数量m
1,n大,m小\(n \geq m, n=10,000, m = 10....1000\),使用逻辑回归或者是没有内核的SVM
2,n小,m中等\(n=1-1,000, m = 10....10,000\),使用带高斯内核的SVM
3,n小,m大\(n=1-1,000, m = 50,000+\),增加特征值,然后使用逻辑回归或者不带内核的SVM(带高斯内核训练会很慢)
PS: 神经网络适用于以上所有情况,可惜训练数据实在太慢
PS: 不带内核的SVM和逻辑回归类似,在使用其中一种时,可以尝试使用另外一种,比较看那个效果好
PS:SVM算法是凸优化问题,总是能找到全局最小或接近它的值
以上只是一种参考方法,重要的还是取决于数据的多少,特征是否足够充分等等其他因素



 浙公网安备 33010602011771号
浙公网安备 33010602011771号