机器学习公开课笔记第五周之优化机器学习算法
一,提高机器学习算法准确度的方法
当我们的机器学习算法不能准确预测我们测试数据时,我们可以尝试通过以下方法提高我们机器学习的算法准确度
1),获得更多的训练样例
2),减少特征数
3),增加特征数
4),增加多项式特征
5),增大或减小\(\lambda\)
二,评估机器学习模型
如果只是单独的使用一个训练集,我们并不能很好的评估机该器学习的算法到底准不准确,因为有可能是过度拟合(Overfitting),我们可以通过把测试集分成两个数据集
取70%作为训练集,30%作为测试集
1),用训练集来学习,获得使\(J(\Theta)\)最小的\(\Theta\)
2),用测试集评估该该算法的准确度
评估算法准确度的方法
1),线性回归,\(J_{test}(\Theta) = \dfrac{1}{2m_{test}} \sum_{i=1}^{m_{test}}(h_\Theta(x^{(i)}_{test}) - y^{(i)}_{test})^2\)
2),逻辑回归,\(err(h_\Theta(x),y) = \begin{matrix} 1 & \mbox{if } h_\Theta(x) \geq 0.5\ and\ y = 0\ or\ h_\Theta(x) < 0.5\ and\ y = 1\newline 0 & \mbox otherwise \end{matrix}\)
\(\text{Test Error} = \dfrac{1}{m_{test}} \sum^{m_{test}}_{i=1} err(h_\Theta(x^{(i)}_{test}), y^{(i)}_{test})\)
三,机器学习算法模型的选择
如果有多个机器学习算法模型可供选择,可以把数据集分成三部分,60%训练集,20%交叉验证即,20%测试集
1),用训练集来学习,获得各个模型使\(J(\Theta)\)最小的\(\Theta\)
2),选出使交叉验证集测试误差最小的模型
3),用测试集评估出第二步所选模型的泛化误差看是否符合我们的要求
四,偏差(Bias or Underfitting)和方差(Variance or Overfitting)
当我们的机器学习模型不能满足我们的要求时,我们改如何提高模型的准确性?虽然有很多方法,但总不能依次尝试,所有方法要么解决高方差要么解决高偏差,所以我们先判断我们的模型是高偏差还是高方差
在线性回归中,当我们提高假设函数方特征x的最高次方d时,偏差和方差是如下图所示变化,高偏差时\(J_{train}^{(\Theta)} \approx J_{CV}^{(\Theta)} \),高方差时\(J_{CV}^{(\Theta)}\) 远大于 \(J_{train}^{(\Theta)} \)

五,正则化参数\(\lambda\)的选取
\(\lambda\)的取值对线性回归模型的影响如下图所示
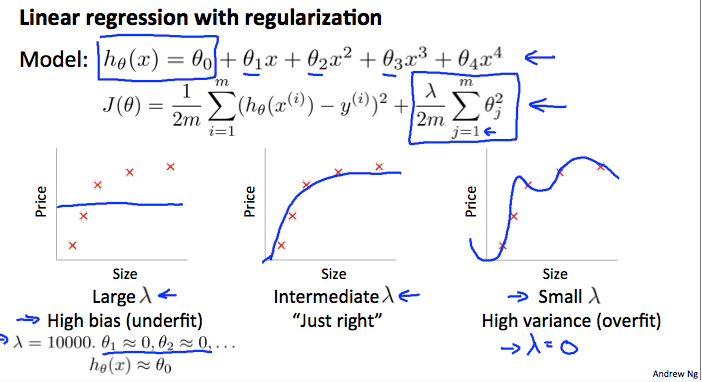
\(\lambda\)太大,偏差高,太小,方差高
选取合适的\(lambda\):
1),创建可供选择的\(lambda\)的数组 (i.e. λ∈{0,0.01,0.02,0.04,0.08,0.16,0.32,0.64,1.28,2.56,5.12,10.24})
2),创建带有不同特征和多项式的次方(degree的大小)的模型集合
3),组合模型集合的模型和\(lambda\)数组的选值,求出\(\Theta\)集合
4),在不加正则化的情况下,选出使\(J_{CV}\)最小的的\(\Theta\)
5),找出第4步所对应的\(lambda\)和模型组合
6),求出\(J_{Test}\)是否符合自己需求
六,学习曲线(Learning Curve)
我们还可以通过学习曲线来判断算法模型是高偏差还是高方差
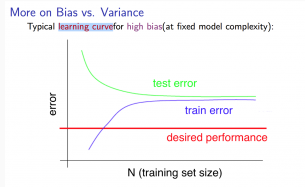
1) 高偏差
当训练数据较少时, \(J_{train}^{(\Theta)} \) 非常小 \(J_{CV}^{(\Theta)} \)非常大
当训练数据增多时, \(J_{train}^{(\Theta)} \) 变大, \(J_{CV}^{(\Theta)} \)变小, \(J_{train}^{(\Theta)} \approx J_{CV}^{(\Theta)} \)
所以当学习模型处于高偏差时,增加训练数据并没有用,如下图所示
2) 高方差
当训练数据较少时, \(J_{train}^{(\Theta)} \) 非常小 \(J_{CV}^{(\Theta)} \)非常大
当训练数据增多时,\(J_{train}^{(\Theta)} \) 变大, \(J_{CV}^{(\Theta)} \)变小,但是\(J_{train}^{(\Theta)} > J_{CV}^{(\Theta)}\),而且他们之间的差距相当明显
所以当学习模型处于高方差时,增加训练数据很有用,如下图所示

七,根据高偏差还是高方差提高机器学习算法准确度的方法
当我们的机器学习算法不能准确预测我们测试数据时,我们可以尝试通过以下方法提高我们机器学习的算法准确度
1),获得更多的训练样例\(\Rightarrow\)修正高方差
2),减少特征数\(\Rightarrow\)修正高偏差
3),增加特征数\(\Rightarrow\)修正高方差
4),增加多项式特征\(\Rightarrow\)修正高方差
5),增大\(\lambda \Rightarrow\)修正高偏差
6),减小\(\lambda \Rightarrow\)修正高方差
八,神经网络的偏差
输入层参数太少会高偏差,计算复杂度低
输入层参数太多会高方差,但可以通过正则化解决,计算复杂度高
使用一层隐藏层是标配,但可以通过增加不同隐藏层数来计算\(J_{CV}^{(\Theta)}\)去交叉验证,然后选择最优方案
总结:
高偏差和高方差是机器学习模型的两端,优秀的机器学习算法模型总是能平衡方差和偏差
交叉验证来选取模型,测试数据评估算法优劣,学习曲线找出模型问题所在,根据问题是高偏差还是高方差选取解决方案



