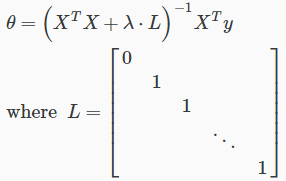机器学习公开课笔记第三周,逻辑回归
1,逻辑回归(Logistic Regression)
监督学习除了线性回归之外,还有逻辑回归(Logistic Regression),也叫分类(Classifycation)
分类问题输入和线性回归问题一样,不过它的输出是离散值。
我们先来学习简单二元分类(输出值只有0和1)
问题就是给定n个特征值Xi,输出它的类别0或1.
因为输出只有0和1,线性回归的假设函数就不适合,需要找一种输出值是0到1的函数,可以使用S函数(Sigmoid Function),也叫逻辑函数(Logistic Function)代替我们的假设函数
\(h_{\theta}(x)= g(\theta ^{T}x)\)
\(z= \theta ^{T}x\)
\(g(z)= \frac{1}{1 + e^{-z}}\)
\(h_{\theta}(x) = g(z)\)
\(g(z)\)函数图如下所示

可以发现0<=\(g(z) = h_{\theta}(x)\)<=1,符合我们的条件,我们可以对半分,根据hθ(x)更靠近0还是1来分类
hθ(x)≥0.5→y=1
hθ(x)<0.5→y=0
或者解释hθ(x)为类1的概率,那么得到如下公式
hθ(x)=P(y=1|x;θ)=1−P(y=0|x;θ)
P(y=0|x;θ)+P(y=1|x;θ)=1
\(z=0\)
\(e^{0}=1 \Rightarrow g(z)=1/2 \)
\(z \to \infty, e^{-\infty} \to 0 \Rightarrow g(z)=1 \)
\(z \to -\infty, e^{\infty}\to \infty \Rightarrow g(z)=0 \)
\(y=1\rightarrow h_{\theta}(x) \geq 0.5 \rightarrow h_{\theta}(x)= \frac{1}{1 + e^{-z}} \geq 0.5\rightarrow \frac{e^{z}}{e^{z} + 1} \geq 0.5\rightarrow \frac{e^{\theta^{T} x}}{e^{\theta^{T} x} + 1} \geq 0.5 \rightarrow \theta^{T} x \geq 0\)
\(y=0 \rightarrow \theta^{T} x < 0\)
z = 0也称为决策边界(Decision Boundary),是分隔0和1的界线
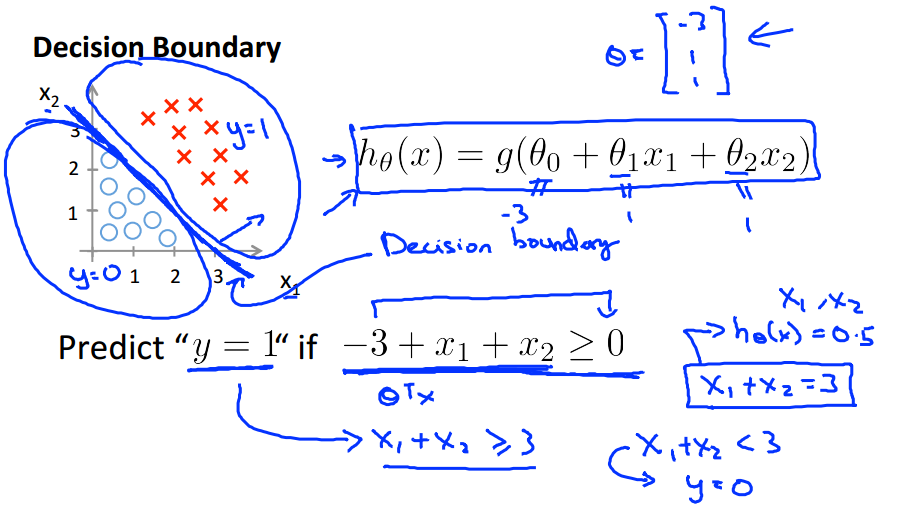
还有可能是非线性多项式的决策边界

2,代价函数(Cost Function)
如果使用类似线性回归的代价函数,在使用梯度下降法的时候,随着\( \theta \)减小,代价函数会出现多个局部最小值,并不能达到全局最小值,是非凸函数,需要另外选代价函数,可以选择如下代价函数

当y=1和0时的代价函数Cost图像如下


无论y=0还是1,hθ(x)都是与y越接近越小,越远越大,符合代价函数的最初定义

y=0和1合并可得单个样例的代价函数

所有样例的代价函数
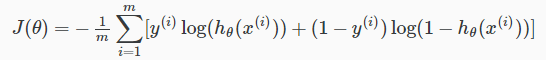
改成向量形式
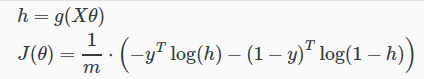
梯度下降法求偏导后

最后结果的公式和线性回归一模一样,除了假设函数hθ(x)
3,我们可以用Octave内部已经集成好的算法,如"Conjugate gradient", "BFGS", and "L-BFGS",来求线性回归和逻辑回归,这些比梯度下降法快的多,而且还不需要选择学习速率α
只需要写一个求代价函数cost的函数

,再调用 fminunc(@costFunction, initialTheta, options)

4,多元分类
当类别为n(>=3)个时,我们可以把它看成n个2元分类问题,取概率最大的hθ(x)


5,解决过度拟合问题

第一幅图是欠拟合(Underfittting),也可叫做高偏差(High Bias),特征太少,无法通过仅有的几个特征模拟线性回归模型
第二幅图是正好,特征正好
第三幅图过度拟合(Overfitting),也可叫做高方差(High Variance),特征太多,构建的模型不仅仅模拟了原有的回归模型,还多出了原本模型不具备的特征
解决过度拟合有两种方法
1) 减少特征值
- 手动去除特征值
- 构建特征选择算法
2) 正则化
- 保留所有特征,减小参数θ
- 每一个特征都对线性模型有细微的影响
6,正则化
当我们有如下假设函数时

可以通过加入λθj2来降低θj
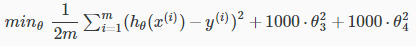
相当于惩罚θj
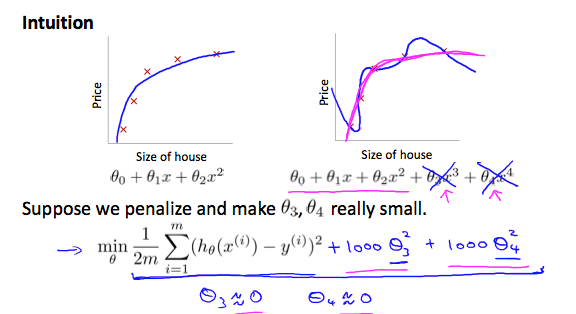
完整正则化公式 ,λ也叫正则参数,后面并有没有θ0

线性回归模型的梯度下降迭代法的正则表达式

移项得到

因为α*λ/m小于1,所以相当于θj减去一个常值,后面就和裸的的线性回归模型一样了
正规方程(Normal Equation)通过如下正则化
当m<=n,加了λ⋅L之后,XTX + λ⋅就可逆了
同理可得,逻辑回归的过度拟合,代价函数和正则化