CSP-S2考前周末刷题班Day4

挑战

题目描述

企鹅豆豆在玩一款叫做 \(Slay the spire\) 的游戏。为了简化游戏，我们将游戏规则魔改如下：

主角一开始血量为 \(H\)，游戏里一共有 \(N\) 个房间，每个房间里有一些怪物，第 \(i\) 个房间需要受到 \(D_i\) 的伤害才能解决所有怪物，解决怪物后会获得对应的 \(C_i\) 的血量恢复，\(C_i\) 严格小于 \(D_i\)，一个房间的怪物只能最多打一次。主角只有在血量为负数时才会死亡，即使血量刚好为 \(0\) 主角也能凭借强大的意志继续打怪。

现在给出每个房间的数据，豆豆想知道他最多能打完多少个房间？

输入格式

从标准输入读入数据。

输入第一行两个正整数 \(N,H\)，表示房间数目和主角的血量。

输入第二行有 \(N\) 个正整数 \(D_i\), 第 \(i\) 个数对应第 \(i\) 个房间。

输入第三行有 \(N\) 个非负整数 \(C_i\), 第 \(i\) 个数对应第 \(i\) 个房间。

输出格式

输出到标准输出。

输出一行一个整数表示最多能打完的房间数目。

样例 \(1\) 输入

4 12
4 8 2 1
2 0 0 0

样例 \(1\) 输出

样例 \(1\) 解释

他可以选择 \(1,3,4\) 号房间。

样例 \(2\)

见下发文件。

子任务
对于 \(30\%\) 的数据， \(1≤N≤10\)。

对于另外 \(10\%\) 的数据， \(C_i=0\)。

对于另外 \(10\%\) 的数据， \(D_i−C_i=1\)。

对于另外 \(30\%\) 的数据， \(1≤N≤1000\)。

对于 \(100\%\) 的数据， \(1≤N≤5×10^3\)。

对于所有数据，\(0≤C_i<D_i≤5000,1≤D_i,H≤5000\)。

Solution

30pts

暴力枚举就可以了。

40pts

\(C_i=0\)。
对于打怪不回血的情况，我们肯定是优先打掉血少的怪。
贪心打怪即可。

50pts

\(D_i-C_i=1\)。
这种情况下打每只怪相当于只掉一滴血，我们按照 \(D_i\) 从大到小贪心打怪即可。

另外\(30pts\)

这个是留给 \(dp\) 写成 \(O(n^3)\) 的同学的。

100pts

排序后背包。
考虑两个关卡 \(x,y\)：
如果 \(x\) 在 \(y\) 前，对 \(y\) 的影响是 \(-D_x+C_x-D_y\)。
如果 \(y\) 在 \(x\) 前，对 \(x\) 的影响是 \(-D_y+C_y-D_x\)。
我们肯定是要让打怪前血越多越好，所以我们应该让 \(C\) 更大的在前面。
所以按照 \(C\) 从大到小，再按照 \(D\) 从大到小。
所以最终打的房间一定是这个顺序，那么我们就可以 \(DP\) 看选还是不选了。
从而转化为一个 \(01\) 背包问题。

#include<algorithm>
#include<iostream>
#include<cstdio>
using namespace std;
inline int read()
{
	char ch=getchar();
	int a=0,x=1;
	while(ch<'0'||ch>'9')
	{
		if(ch=='-') x=-x;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
	{
		a=(a<<1)+(a<<3)+(ch^48);
		ch=getchar();
	}
	return a*x;
}
const int N=5005;
int n,m,ans;
int dp[N];
struct node
{
	int a,b;
}a[N];
bool cmp(node x,node y)
{
	if(x.b==y.b) return x.a>y.a;
	return x.b>y.b; 
}
int main()
{
	n=read();m=read();
	for(int i=1;i<=n;i++) a[i].a=read();
	for(int i=1;i<=n;i++) a[i].b=read();
	sort(a+1,a+1+n,cmp);    //按照回血从大到小排序,再按照掉血从大到小排序 
	for(int i=1;i<=n;i++)   //01背包的过程 
	{
		for(int j=a[i].a;j<=m;j++)
		{
			dp[j-a[i].a+a[i].b]=max(dp[j-a[i].a+a[i].b],dp[j]+1);
		}
	}
	for(int i=0;i<=m;i++)
	    ans=max(ans,dp[i]);
	printf("%d\n",ans);
	return 0;
}

航班复杂度

题目描述

企鹅国有 \(N\) 座城市和 \(M\) 条不同的航班，每条航班都有指定的起点 \(u_i\) 和终点 \(v_i\)，乘坐这个航班可以从城市 \(u_i\) 到达城市 \(v_i\)，但是不能从 \(v_i\) 到 \(u_i\)，也就是这个航班是单向的。

企鹅豆豆最近被企鹅航空抽中成为 \(SSSSVIP\),并获得了 \(L\) 张航班卷，一张航班卷可以免费乘坐一次航班。企鹅豆豆迫不及待地要开始他的环国之旅，他会根据自己心情随意选择一个起点城市，然后连续乘坐 \(L\) 次航班。对于每种连续乘坐航班的方案，我们会记录他到达每个城市的顺序，生成一个对应的序列，比如 \(3,2,3\) 表示他乘坐了两次航班，从 \(3\) 号城市飞到 \(2\) 号城市再飞到 \(3\) 号城市。两个连续乘坐航班方案不同，当且仅当对应的序列不同。

企鹅豆豆现在现在想知道他最多能有多少种不同的连续航班乘坐方案。但是由于 \(L\) 实在是太太太大了，所以答案 \(Ans\) 也非常非常大，所以他并不想求出具体值，他发明了一个叫做航班复杂度的计量方式——我们称航班复杂度是整数 \(k\)，当且仅当存在常数 \(c\) 使得对于充分大的 \(L\), \(cL^k>Ans\)（注意 \(Ans\) 也是会随 \(L\) 的增大而增大）。

豆豆现在想知道，当前的航班复杂度 \(k\) 最小能是多少?

输入格式

从标准输入读入数据。

第一行两个正整数 \(N,M\)，表示城市数目和航班数。

接下里 \(M\) 行，每行两个正整数 \(u_i,v_i(u_i≠v_i)\) 描述一个航班。

输出格式

输出到标准输出。

输出一行一个整数 \(k\) 表示答案。如果不存在任何整数 \(k\) 满足要求，请输出 \(-1\)。

样例 \(1\) 输入

样例 \(1\) 输出

样例 \(1\) 解释

由于从任意城市出发坐 \(L\) 次航班只有一种方案，所以令常数 \(c=2\) 有 \(cL^0>1\)，且不存在更小的整数 \(k\) 满足这个要求。

样例\(2\)

见下发文件。

子任务

对于 \(15\%\) 的数据，航班形成多个不相交的环。
对于另外 \(15\%\) 的数据，如果存在航班 \((u_i,v_i)\) 则存在航班 \((v_i,u_i)\)。

对于另外 \(15\%\) 的数据，航班形成的简单环只有两个，以及一些不形成环的航班。

对于另外 \(20\%\) 的数据，\(1≤n≤100,1≤m≤300\)。

对于另外 \(20\%\) 的数据，\(1≤n≤1000,1≤m≤3000\)。

对于另外 \(5\%\) 的数据，\(m=5\)。

对于 \(100\%\) 的数据，\(1≤n,m≤10^5\)。

Solution

题意理解：
你可以任选一个点，然后连续走 \(L\) 步，有若干方案数，在所有点对应的方案数中找出最大值，这个方案数能表达成 \(cL^{k}\) 的形式，输出 \(k\)。

30pts

对于前 \(15\%\) 的数据，有多个不相交的环。
显然和样例一样，答案是个常数。那么 \(k=0\)。
良心保底，输出 \(0\) 即有 \(30\) 分。

45pts

如果存在航班 \((u_i,v_i)\) 则存在航班 \((v_i,u_i)\)。
就是说保证边有来有回。
我们画个图理解一下：

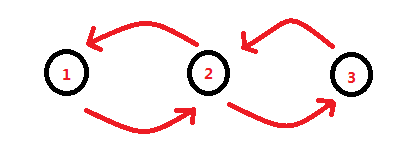
假如我们在 \(1\) 号点，我们先顺着 \(<1,2>\) 走到了 \(2\) 号点，此时我们面临着两种选择：一个是沿着 \(<2,1>\) 回到 \(1\) 号点，一个是沿着 \(<2,3>\) 走到 \(3\) 号点，但无论是选择哪种，当我们走完之后，都只能再次回到 \(2\) 号点，然后我们又再次面临两种选择。
也就是说，我们每走两条边就有两种方案可以选择，那么最后的方案数就是 \(2^{⌊\frac{L}{2}⌋}\)。
显然方案数是指数级的。
指数的增长是爆炸的，当 \(L\) 足够大时，你找不到一个 \(k\) 使得 \(2^{⌊\frac{L}{2}⌋}<L^k\)，应当输出 \(-1\)。
你意识到了一个很重要的结论：
如果有两个环相交形成一个“8”字型，那么这个题的答案就是 \(-1\) 了。
那么把这个条件判掉之后，这个图中就没有复杂的环了。

60pts

航班形成的简单环只有两个，以及一些不形成环的航班。
对于只有两个简单环的情况，考虑两种情况：
第一种是两个环间毫无瓜葛，这就和多个不相交的环一样；
第二种是一个环能到达另一个环，但是另一个环无法返回这个环：
对于这种情况，路径一定是现在第一个环上绕若干圈，再通过一条边又在另一个环上绕若干圈。
我们可以看作是在一个长度为 \(L\) 的区间上，你枚举一个分界点 \(i\)，前 \(i-1\) 步是在第一个环上走的，后 \(L-i\) 步是在第二个环上走的，且两个环上的路径是固定的。由于而且每个可作为分界点的地方都是相差第一个环的环长的。
假如第一个环的环长为 \(t\)，那么一共有 \(\frac{L}{t}\) 个分界点，由于 \(t\) 是个常数，所以这个方案数就是 \(O(L)\) 级别的，那么 \(k=1\)。

65pts

\(m=5\)。
这一部分分是拿给你手玩的，要你把所有 \(m=5\) 的情况画一画。
如果你玩出来了说不定就 \(AC\) 了。

100pts

讲到这里就很接近标算了，无非就是扩展到好几个环在这里绕。
假如我们有三个环，无非就是把区间砍两刀，分成的三段分别对应在哪个环上绕的路径。砍第一刀有 \(O(L)\) 的选择，砍第二刀也有 \(O(L)\) 的选择，所以总的方案数就是 \(O(L^2)\)。
那么做法就很明显了：
我们先把每个简单环缩成一个点，只保留环与环之间的连边，我们会得到一个 \(DAG\)。如果图上的最长路径为 \(k\)，那么答案为 \(k\)。
原因如下：这条路径是由一系列长度固定的环和环之间直接连边组成，我们一个长度为 \(L\) 的路径唯一可以选择的是在一个环上绕几圈再到下一个环。例如一个长度为 \(1\) 的路径，即对应了原图一个简单环和另一个简单环以及第一个环到第二个环之间的连边。

#include<algorithm>
#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
inline int read()
{
	char ch=getchar();
	int a=0,x=1;
	while(ch<'0'||ch>'9')
	{
		if(ch=='-') x=-x;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
	{
		a=(a<<1)+(a<<3)+(ch^48);
		ch=getchar();
	}
	return a*x;
}
const int N=2e5+5;
int n,m,top,tim,edge,Edge,Scc,Ans;
int head[N],Head[N],in[N],dfn[N],low[N],vis[N],s[N],scc[N],size[N],Size[N];
struct node
{
	int from,nxt,to;
}a[N],e[N];
void add(int from,int to)
{
	edge++;
	a[edge].from=from;
	a[edge].to=to;
	a[edge].nxt=head[from];
	head[from]=edge;
}
void Add(int from,int to)
{
	Edge++;
	e[Edge].from=from;
	e[Edge].to=to;
	e[Edge].nxt=Head[from];
	Head[from]=Edge;
}
void tarjan(int u)
{
	dfn[u]=low[u]=++tim;
	s[++top]=u;
	vis[u]=1;
	for(int i=head[u];i;i=a[i].nxt)
	{
		int v=a[i].to;
		if(!dfn[v])
		{
			tarjan(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(dfn[u]==low[u])
	{
		Scc++;
		while(s[top+1]!=u)
		{
			scc[s[top]]=Scc;
			vis[s[top]]=0;
			size[Scc]++;
			top--;
		}
	}
}
struct Node
{
	int u,ans;
};
bool Check()                      //判断是否有"8"字形的方法：如果联通块内点数不等于边数就说明有"8"字形          
{
	for(int i=1;i<=edge;i++)
	{
		int u=a[i].from;
		int v=a[i].to;
		if(scc[u]==scc[v]) Size[scc[u]]++;  //两个点都在同一联通块内,则贡献一条边 
	}
	for(int i=1;i<=Scc;i++)
	{
		if(size[i]==1) continue;  //只有一个点的连通块不作考虑 
		if(Size[i]!=size[i]) return 1;
	}
	return 0;
}
queue<Node> q;
int main()
{
	n=read();m=read();
	for(int i=1;i<=m;i++)
	{
		int u=read();
		int v=read();
		add(u,v);
	}
	for(int i=1;i<=n;i++)         //缩点,把简单环缩成一个点 
	    if(!dfn[i]) tarjan(i);
	if(Check())                   //判断是否有"8"字形 
	{
		printf("-1\n");
		return 0;
	}
	for(int i=1;i<=edge;i++)      //重新连边 
	{
		int u=a[i].from;
		int v=a[i].to;
		if(scc[u]==scc[v]) continue;
		Add(scc[u],scc[v]);
		in[scc[v]]++;             //统计入度 
	}
	for(int i=1;i<=Scc;i++)
	    if(!in[i])                //把入度为0的点放入队列中 
	    {
	    	if(size[i]>1) q.push((Node){i,1});  //Node第二维表示经过了多少个简单环 
	    	else q.push((Node){i,0});
		}
	while(!q.empty())
	{
		Node u=q.front();
		q.pop();
		Ans=max(Ans,u.ans);       
		for(int i=Head[u.u];i;i=e[i].nxt)
		{
			int v=e[i].to;
			q.push((Node){v,u.ans+(size[v]>1)});  //如果这个是简单环,别忘了ans++ 
		}
	}   
	printf("%d\n",Ans-1);        //最长路上有Ans个简单环,答案就是Ans-1 
	return 0; 
}

数据生成器

题目描述

豆豆正在熬夜造下周NOIP模拟赛的数据。

他在写一道“求一个数列最长连续不下降子串的长度”的数据生成器, 第i个整数的生成范围是 \([L_i,R_i]\)。

他想知道生成的数列的答案最大能是多少？

这里 最长连续不下降子串 是指原序列最长的连续区间，该区间内数值单调不减。

输入格式

从标准输入读入数据。

输入第一行两个整数 \(N\)，表示数列长度。

接下来 \(N\) 行，每行两个数 \(L_i\) 和 \(R_i\)。

输出格式

输出到标准输出。

输出一行一个整数表示最大的答案。

样例 \(1\) 输入

样例 \(1\) 输出

样例 \(1\) 解释

一个可能的数列为：
\(6,3,5,5,7,3\)

样例 \(2\)

见下发文件。

子任务

对于 \(10\%\) 的数据，\(N≤10,1≤L_i≤R_i≤6\)。
对于 \(30\%\) 的数据，\(N≤300\)。
对于 \(40\%\) 的数据，\(N≤2000\)。
对于 \(70\%\) 的数据，\(N≤100000\)。
对于 \(100\%\) 的数据，\(N≤3000000,1≤L_i≤R_i≤10^9\)。
请选手选择较快的读入方式。

Solution

10pts

暴力枚举检查即可。

30pts

枚举最终答案是哪段区间，然后 \(O(N)\) 检查即可。

40pts

枚举答案区间的起点，然后看向后最多能扩展多远。

70pts

线段树优化 \(DP\) 即可。复杂度 \(O(N\log{N})\)。

100pts

令 \([L,R]\) 为一个单调不下降区间。
我们发现，如果目前的 \(R\) 最左能延伸到 \(L\)，那么我们将 \(R\) 右移一位后最左最多也只能延伸到 \(L\)，这样 \(L\) 就是单调的。
而我们考虑目前最多能延伸到哪里，发现如果 \([L,R]\) 合法，那么 \(R\) 点的 \(R_i>\) 区间内所有位置 \(L_i\) 的最大值。
就可以单调队列优化了：我们用单调队列维护每个点的左端点，计算答案前要先把左端点比当前点的右端点大的全部弹出（不能保证是单调不降了），这样最靠左的符合条件的点就是它所能向左扩展的最远距离。
时间复杂度 \(O(N)\)。

#include<iostream>
#include<cstdio>
#include<cmath>
#define ll long long
using namespace std;
inline ll read()
{
	char ch=getchar();
	ll a=0;
	while(ch<'0'||ch>'9') ch=getchar();
	while(ch>='0'&&ch<='9') a=(a<<1)+(a<<3)+(ch^48),ch=getchar();
	return a;
}
const int N=3e6+5;
int n,h,t,ans;
int l[N],r[N],q[N],dp[N];
int main()
{
	n=read();
	for(int i=1;i<=n;i++) 
	{
		l[i]=read();
		r[i]=read();
		dp[i]=i;                        //dp[i]表示第i个点所能向左扩展的最左边的点 
	}
	h=1;ans=1;
	for(int i=1;i<=n;i++)
	{	
		while(h<=t&&l[q[h]]>r[i]) h++;  //统计答案前先把左端点大于当前右端点的弹出队列(不弹出的话无法维护序列不降的性质) 
		if(h<=t) ans=max(ans,i-dp[q[h]]+1);  //当前点的答案:这个点到队头所能扩展的最左边的点的距离 
		while(h<=t&&l[i]>=l[q[t]]) dp[i]=dp[q[t]],t--;  //如果当前点的左端点比队尾的大,那么完全可以把队尾弹出(左端点最大值不会从它产生),但注意要继承它最远的扩展点 
		q[++t]=i;
	}
	printf("%d\n",ans);
	return 0;
}

排列组合

题目描述

企鹅豆豆最近沉迷排列无法自拔，他现在有一个长度为 \(N\) 的排列，他现在拥有神力每次可以把这个排列的一个非空区间里所有数字变成这个区间数字的最大值。比如他可以对于 \(1,3,2,4\) 的 \([3,4]\) 区间进行这个操作，使之变为 \(1,3,4,4\)。

他喜欢没见过的排列，所以他想知道通过不超过 \(K\) 个这样的操作，可以把一个排列变成多少种不同的序列？

一个长度为 \(N\) 排列是指一个长度为 \(N\) 含有正整数 \(1\) 到 \(N\) 且任意两个不同位置的数字不相同的序列。两个序列不同当且仅当他们有一个位置上的数值不同。

输入格式

从标准输入读入数据。

输入第一行两个整数 \(N\) 和 \(K\)，表示排列的长度以及最多的操作次数。

接下来一行 \(N\) 个正整数表示这个排列。

输出格式

输出到标准输出。

输出一行一个非负整数表示所有能够变成的不同的序列个数。由于答案可能会非常大，所以你需要把答案对 \(998244353\) 取模。

样例 \(1\) 输入

3 2
3 1 2

样例 \(1\) 输出

样例 \(1\) 解释

所有可能的序列有：

\(3,1,2\) (可以不操作)
\(3,2,2\)
\(3,3,2\)
\(3,3,3\)

样例 \(2\)

见下发文件。

样例 \(3\)

见下发文件。

子任务

对于 \(1−6\) 号测试点，第 \(i\) 个测试点保证 \(N=2i\)。

对于 \(7−8\) 号测试点，保证 \(K=1\)。

对于 \(9−12\) 号测试点，保证序列严格上升，且 \(9,10\) 测试点 \(N=K\)。

对于 \(13−14\) 号测试点，保证 \(N,K≤20\)。

对于 \(15−16\) 号测试点，保证 \(N,K≤50\)。

对于 \(17−18\) 号测试点，保证 \(N,K≤100\)。

对于所有数据保证 \(1≤N≤200,0≤K≤200\)。

Solution

30pts

\(N=2i\)，也就是说 \(N\) 最大也就是 \(12\)。
数据范围小，爆搜加点剪枝就可以过了。

40pts

\(K=1\)。
可以 \(n^2\) 枚举我们操作哪个区间，改完之后再去看看这种操作区间是不是和之前的一样就好了。

60pts

序列严格上升，且 \(9,10\) 测试点 \(N=K\)。
这种情况也就是说我们没有限制，想操作多少次都行。
枚举最后一个数它所占的区间有多长，剩下的区间已经算过了，可以递推搞定。
对于 \(11,12\) 测试点，可能 \(K\) 没有那么多。
我们可以 \(dp\) 记一下我们现在操作了多少次，方案数有多少种，一个简单的 \(dp\) 就可以拿到。

70pts

\(N,K<=20\)。
这一部分是留给写了\(O(n^5)\) 的同学的。

100pts

假如我们有一个序列：
\(9,7,3,1,2,5,4,6,8\)
然后我们一顿操作形成了下面的这个序列：
\(9,9,9,1,5,5,6,6,8\)
现在我们来讨论所形成的序列会有哪些约束，如果我们能把所有的约束条件列出来，这样就变成了一个找序列的任务了，而不是我们在这怎么操作的事了。
首先我们来看看哪些位置保留了：

发现某些数原位置一定得对得上。而且对得上的这些位置的顺序完全取决于原数列它们的位置。
比如上面的例子，操作后的序列能与原序列对得上的数依次为：\(9,1,5,6,8\)，可以发现它们在原数列也是按照这个顺序出现的。
这就保证了我们不可能搞出这么一个序列：\(9,1,9,1,5,5,6,6,8\)。
还可以这么描述：每一个数得区间一定是一个连续的区间。
我们再来写一个满足上面条件的错误序列：
\(7,7,7,1,5,5,6,6,8\)
虽说每个数与原位置对应，且都是连续的，但是不可能用 \(7\) 去覆盖 \(9\)（即第一个位置不可能是 \(7\)），所以说这个序列也是不合法的。
也就是说，它所能覆盖的区间里的数都要比它小。
记一个 \(L_i\) 和 \(R_i\) 表示 \(i\) 覆盖的区间左端点和右端点。
到这里我们把操作序列所要满足的性质列举一下：
1.位置相对不变。
2.\([L_i,R_i]\)内都要小于这个数。
3.最少的操作次数 \(k\) 的算法：操作序列有多少种不同的值 \(-\) 长度为 \(1\) 且在原位置的数个数。例如：\(9,9,9,1,6,6,6,8,8\) 可以由原序列最少操作 \(4-1=3\) 次得到。
有这几个性质之后我们就可以尝试去 \(dp\) 了，就可以求出在满足这三个条件的情况下有多少个序列。
\(f[i][j][k]\) 表示已经决定 \(A\) 中前 \(i\) 个元素在 \(S\) 中的位置，\(S\) 中前 \(j\) 个位置已经被占领，剩下 \(k\) 次操作的方案数。
考虑我们接下来可能会有这几种操作：
1.如果 \(a_{i+1}\) 不参与序列，转移到 \(f[i+1][j][k]\)。
2.如果 \(a_{i+1}\) 参与序列匹配，枚举 \(S\) 后面接几个 \(a_{i+1}\) （同时要检查能不能放）。根据情况决定是否消耗操作次数（原位置长度为 \(1\)，不消耗）。
时间复杂度 \(O(n^4)\)。

#include<iostream>
#include<cstdio>
#define ll long long
using namespace std;
inline int read()
{
	char ch=getchar();
	int a=0;
	while(ch<'0'||ch>'9') ch=getchar();
	while(ch>='0'&&ch<='9') a=(a<<1)+(a<<3)+(ch^48),ch=getchar();
	return a;
}
const int N=205;
const int M=998244353;
int n,K;
int a[N],l[N],r[N];
ll dp[N][N][N],ans;
int main()
{
	n=read();K=read();
	for(int i=1;i<=n;i++) a[i]=read();
	for(int i=1;i<=n;i++)  //预处理每个点的l和r 
	{
		int j;
		for(j=i;j>=1;j--)   
			if(a[j]>a[i])
                break;
        l[i]=j+1;
        for(j=i;j<=n;j++)
            if(a[j]>a[i])
                break;
        r[i]=j-1;
	}
	dp[1][1][0]=1;         //边界:确定好了原数列的第一个数和操作数列的第一个数,操作了0次方案数 
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n+1;j++)  //注意,我们是算一个状态对其他状态的贡献,所以可能会转移到操作序列的n+1位 
		{
			for(int k=0;k<=K;k++)
			{
				if(!dp[i][j][k]) continue;  //这个状态的方案数本来就是0,就不会对其他状态产生贡献 
				dp[i+1][j][k]=(dp[i+1][j][k]+dp[i][j][k])%M; //如果原序列的第i+1位a[i+1]没有在操作序列中出现,直接转移到dp[i+1][j][k] 
				if(j<l[i]) continue;  //操作序列的第j个位置不能被a[i]扩展到 
				for(int pos=j;pos<=r[i];pos++)  //枚举a[i]能扩展到哪,注意只需要从j开始就好了,因为比j更小的已经考虑过了 
				{
					int nk=k+1;    //一般来说需要k+1次操作 
					if(j==i&&pos==i) nk--;  //如果你从原位置开始扩展,并扩展到了原位置,说明你把原位置的a[i]直接保留了下来,是不消耗次数的 
					dp[i+1][pos+1][nk]=(dp[i+1][pos+1][nk]+dp[i][j][k])%M;  //[j,pos]都被扩展成了a[i],转移到dp[i+1][pos+1][k+1] 
				}
			}
		}
	}
	for(int k=0;k<=K;k++)     //枚举所有可能的操作的次数 
	    ans=(ans+dp[n+1][n+1][k])%M;  //注意前两维的答案统计到了n+1 
	printf("%lld\n",ans);
    return 0;
}

一个小优化。
设置状态 \(f[i][j][k][0/1]\) 表示已经决定 \(A\) 中前 \(i\) 个元素在 \(S\) 中的位置，\(S\) 中前 \(j\) 个位置已经被占领，剩下 \(k\) 次操作的方案数，当然每个 \(a_i\) 值最多算作一次操作，用一维记录是否已经消耗了操作（\(0\) 表示没有）。
如果 \(S_j\) 接着接一个 \(a_i\)，检查操作合法后，转移到 \(f[i][j+1][k][1]\) 或者 \(f[i][j+1][k+1][1]\)（取决于原状态的 \(0/1\) 和情况判定）。
如果 \(S_j\) 不再接 \(a_i\)，转移到 \(f[i+1][j][k][0]\)。
时间复杂度 \(O(n^3)\)。

posted @ 2020-10-31 20:00 暗い之殇阅读(190) 评论(1) 编辑收藏举报

刷新页面返回顶部

暗い之殇

你要记得，紫檀未灭，我亦未去。

CSP-S2考前周末刷题班Day4

挑战

题目描述

输入格式

输出格式

样例 \(1\) 输入

样例 \(1\) 输出

样例 \(1\) 解释

样例 \(2\)

Solution

30pts

40pts

50pts

另外\(30pts\)

100pts

航班复杂度

题目描述

输入格式

输出格式

样例 \(1\) 输入

样例 \(1\) 输出

样例 \(1\) 解释

样例\(2\)

子任务

Solution

30pts

45pts

60pts

65pts

100pts

数据生成器

题目描述

输入格式

输出格式

样例 \(1\) 输入

样例 \(1\) 输出

样例 \(1\) 解释

样例 \(2\)

子任务

Solution

10pts

30pts

40pts

70pts

100pts

排列组合

题目描述

输入格式

输出格式

样例 \(1\) 输入

样例 \(1\) 输出

样例 \(1\) 解释

样例 \(2\)

样例 \(3\)

子任务

Solution

30pts

40pts

60pts

70pts

100pts

公告