S2考前综合刷题营Day7
water
题目描述
有一个长为 \(n\) 的序列 \(a_i\),小 \(Y\) 希望数字总共不超过 \(k\) 种。
为了达到这个目的,她可以把任意位置修改成任意数,这个操作可以进行任意多次。
请你帮她求出最少需要修改几个位置可以达成目的。
输入格式
第一行两个整数 \(n,k\)。
接下来一个 \(n\) 个整数 \(a_i\)。
输出格式
一行一个整数表示答案。
样例输入
5 2
2 2 1 1 5
样例输出
1
样例解释
把 \(5\)(第 \(5\) 个位置的数)改成 \(1\) 或 \(2\) 就行了。
数据范围
对于 \(30\%\) 的数据,\(n≤20\)。
对于另外 \(30\%\) 的数据,\(n≤5000\)。
对于所有数据,满足 \(1≤k≤n≤200000,1≤a_i≤n\)。
Solution
100pts
一个很显然的贪心思路:我们一定是把出现次数少的数改成出现次数多的数。
模拟一下就好了。
#include<algorithm>
#include<iostream>
#include<cstdio>
#define ll long long
using namespace std;
const int N=1e6;
int n,m,k,x;
int cnt[N],ans[N];
ll sum;
bool cmp(int x,int y)
{
return x<y;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d",&x);
cnt[x]++; //统计每个数出现了多少次
}
for(int i=1;i<=n;i++)
{
if(cnt[i]) ans[++k]=cnt[i];//把每个数出现的次数装在ans数组里
}
if(k<=m) printf("0\n"); //如果本来就不够m种,就不用删数了
else
{
sort(ans+1,ans+1+k,cmp); //贪心从小到大排序
for(int i=1;i<=k-m;i++) sum+=ans[i]; //删掉最少的k-m个
printf("%lld\n",sum);
}
return 0;
}
circle
题目描述
如果你听过我今年的冬令营营员交流讲课,那么这将会是一道水题。
有一个 \(1..n\) 依次连成的环,有一个从 \(1\) 开始移动的指针,每次指针所在位置有 \(p\) 的概率消失并将这个位置对应的下标$(在 \(1..n\) 中\()\) 插入序列 \(B\) 的末尾,然后指针移动一格\((1\) 移到 \(2\),\(n\) 移到 \(1\) 这样,一个位置若已经消失则不会被移动到\()\)。所有位置都消失时游戏结束。
最后 \(B\) 会是一个排列,你需要求出 \(B\) 的逆序对的期望,对 \(998244353\) 取模。
输入格式
一行三个整数 \(n,x,y\)。概率 \(p=\frac{x}{y}\)。
输出格式
一行一个整数表示答案。
样例输入
4 1 2
样例输出
2
样例解释
因为一些原因,本题不提供样例解释。
数据范围
对于 \(30\%\) 的数据,\(n≤10\)。
对于 \(40\%\) 的数据,\(n≤15\)。
对于 \(50\%\) 的数据,\(n≤20\)。
对于所有数据,\(1≤n≤10^8,0<x<y≤10^9\)。
Solution
求排列的逆序对数量和的期望,我们可以把算每一对逆序对的期望和。
注意到每个逆序对的贡献是相同的。
所以我们先考虑 \(n=2\) 的情况:这时候只有两个数 \(1\) 和 \(2\),那么要产生逆序对肯定是 \(2\) 先消失然后 \(1\) 再消失。
我们枚举当指针循环了 \(t\) 轮后,\(2\) 才消失,对于 \(2\) 所贡献的概率就是:\(q^{t}p(q=1-p)\),\(1\) 肯定是在第 \(t+1\) 轮消失,那么 \(1\) 的概率就是:\(q^{t+1}*1\),所以循环 \(t\) 轮的逆序对的期望就是:\(q^{2t+1}p\)。
所以我们枚举 \(t\),就可以求出总答案了:\(\sum_{t}q^{2t+1}p\)。
那...这个要怎么求呢?是个等比数列求和:
\(\sum_{t}q^{2t+1}p=p*(q^1+q^3+...+q^{2t+1})=p*\frac{q^1(1-q^{2t})}{1-q^2}\)
由于 \(\lim\limits_{t \rightarrow +\infty} q^{2t}=0(q=1-p<1)\),所以上面那个式子的极限就是:\(\frac{pq}{1-q^2}\)
一共有 \(\frac{n(n-1)}{2}\) 个逆序对,每一个逆序对产生的概率是 \(\frac{pq}{1-q^2}\),所以答案就是:\(\frac{pqn(n-1)}{2(1-q^2)}\)。
注意膜意义下不能做除法,所以要求逆元。
\(\frac{pq}{1-q^2}=\frac{pq}{1-(1+p^2-2p)}=\frac{pq}{2p-p^2}=\frac{q}{2-p}=\frac{\frac{y-x}{y}}{\frac{2y-x}{y}}=\frac{y-x}{2y-x}\)。
输出:\(\frac{1}{2}*(y-x)*n*(n-1)*Inv(2y-x)\) 即可。
#include<iostream>
#include<cstdio>
#define ll long long
using namespace std;
const ll N=1e8+5;
const ll M=998244353;
ll n,x,y;
ll quick_pow(ll a,ll b) //快速幂
{
ll ans=1;
while(b)
{
if(b&1) ans=ans*a%M;
a=a*a%M;
b>>=1;
}
return ans;
}
ll inv(ll x) //利用费马小定理求x的逆元
{
return quick_pow(x,M-2);
}
int main()
{
scanf("%lld%lld%lld",&n,&x,&y);
ll t=(n*(n-1)/2)%M;
ll a=t*(y-x+M)%M;
ll b=(2*y-x+M)%M; //求2y-x的逆元
printf("%lld\n",a*inv(b)%M); //输出答案
return 0;
}
path
题目描述
有一个 \(n\) 个点 \(m\) 条边的 \(DAG\)(有向无环图),定义一条经过 \(x\) 条边的路径的权值为 \(x_k\)。
对于 \(i=1...n\),求出所有 \(1\) 到 \(i\) 的所有路径的权值之和, 对 \(998244353\) 取模。
输入格式
第一行三个整数 \(n,m,k\)。
接下来 \(m\) 行,每行两个整数 \(u,v\),描述一条 \(u\) 到 \(v\) 的有向边。
输出格式
\(n\) 行,每行一个整数表示答案。
样例输入
5 7 3
1 2
1 3
2 4
3 5
2 5
1 4
4 5
样例输出
0
1
1
9
51
数据范围
对于 \(20\%\) 的数据,\(n≤2000,m≤5000\)。
对于另外 \(10\%\) 的数据,\(k=1\)。
对于另外 \(20\%\) 的数据,\(k≤30\)。
对于所有数据,满足 \(n≤100000,m≤200000,0≤k≤500\)。
数据有梯度。
Solution
先讲暴力。\(dp[u][i]\) 表示 \(1\) 到 \(u\) 的所有路径边数的 \(i\) 次方的和。答案就是 \(dp[u][k]\)。
转移就对于每条边 \(u->v\),\(dp[v][i]+=\sum_{j}dp[u][j]{i\choose j}\)
复杂度 \(O(mk^2)\)。
优化的话:
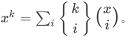
也就是说 \(dp[u][i]\) 表示 \(1\) 到 \(u\) 的所有路径边数的 \(i\) 次下降幂的和,最后用 \(stirling\) 数还原出答案。
第 \(2\) 类 \(stirling\) 数可以递推预处理,是经典问题。
转移就对于每条边 \(u->v\),\(dp[v][i]+=dp[u][i-1]+dp[u][i]\)。
复杂度 \(O(mk)\)。
#include<cstdio>
#include<cstring>
#include<vector>
#include<queue>
#include<iostream>
#include<algorithm>
#include<ctime>
#include<cassert>
#define rep(i,a,b) for (int i=a; i<=b; i++)
#define per(i,a,b) for (int i=a; i>=b; i--)
typedef long long ll;
using namespace std;
typedef pair<int,int> Pii;
typedef vector<int> vec;
inline void read(int &x) {
x=0; char c=getchar(); int f=1;
while (!isdigit(c)) {if (c=='-') f=-1; c=getchar();}
while (isdigit(c)) {x=x*10+c-'0'; c=getchar();} x*=f;
}
const int N = 202000, mo = 998244353;
const ll mod = (0x7fffffffffffffffLL / mo - mo)/503*mo;
ll dp[100005][502],s[505][505];
int n,m,K,q[N],deg[N];
int head[N],edgenum,nxt[N<<1],to[N<<1];
inline void add(int u, int v) {
to[++edgenum]=v; nxt[edgenum]=head[u]; head[u]=edgenum; deg[v]++;
}
inline void topsort() {
int f=1,r=1; rep(i,1,n) if (!deg[i]) q[r++]=i,dp[i][0]=1;
while (f!=r) {
int u=q[f++]; //printf("dot %d\n",u);
for (int i=head[u]; i!=0; i=nxt[i]) {
int v=to[i]; deg[v]--; if (!deg[v]) q[r++]=v;
ll *p1=dp[u];
ll *p2=dp[u];
rep(k,0,K) {
ll &tmp=dp[v][k];
if (k==0) tmp+=(*p1);
else {p1++; tmp+=(*p1)+(*p2)*k; p2++;}
// tmp+=dp[u][k]+(k==0?0:k*dp[u][k-1]);
if (tmp>=mod) tmp%=mod;
}
}
}
}
int main() {
read(n); read(m); read(K);
s[0][0]=1;
rep(i,1,500) rep(j,1,i) s[i][j]=(s[i-1][j-1]+1LL*s[i-1][j]*j)%mo;
rep(i,1,m) {int x,y; read(x); read(y); add(x,y);}
topsort();
rep(i,1,n) {
ll ans=0; rep(j,0,K) ans+=s[K][j]*(dp[i][j]%mo)%mo;
printf("%lld\n",ans%mo);
}
return 0;
}
point
题目描述
你有 \(n\) 条直线,直线用 \(A_ix+B_iy=C_i\) 来表示。为了减少细节,保证这 \(n\) 条直线以及 \(x\) 轴、\(y\) 轴两两都有恰好 \(1\) 个交点。
现在这 \(n\) 条直线两两的交点处产生了一个人,现在总共有 \(\frac{n(n−1)}{2}\) 个人。
你需要找到一个点 \(P\),使其距离所有人的曼哈顿距离和最小。若有多个满足条件的点,选择 \(x\) 坐标最小的,若仍有多个,选择 \(y\) 坐标最小的。
输入格式
第一行一个正整数 \(n\)。
接下来 \(n\) 行,每行三个整数 \(A_i,B_i,C_i\)。
输出格式
一行两个实数表示答案,请保留 \(6\) 位小数输出。
样例输入
3
1 1 1
2 -1 2
-1 2 2
样例输出
1.000000 1.000000
数据范围
对于 \(20\%\) 的数据,\(n≤1000\)。
对于 \(40\%\) 的数据,\(n≤5000\)。
对于所有数据,满足 \(n≤40000,|A_i|,|B_i|,|C_i|≤10000\)。
Solution
答案的 \(x\) 坐标即为所有人的中位数, \(y\) 坐标也同理。
二分答案,就是要数有几个人在 \(mid\) 左侧。
在 \(-∞\) 处按直线高度排序,那么随着 \(x\) 变大,直线会产生交点,也就是说直线高度大小关系会改变。
发现这个交点个数就是逆序对个数,这个可以画图理解。
树状数组统计就好了。
时间复杂度 \(O(n\log{\log{V}})\)。
#include<bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define mp make_pair
#define SZ(x) ((int)x.size())
#define ALL(x) x.begin(),x.end()
#define L(i,u) for (register int i=head[u]; i; i=nxt[i])
#define rep(i,a,b) for (register int i=(a); i<=(b); i++)
#define per(i,a,b) for (register int i=(a); i>=(b); i--)
using namespace std;
typedef long double ld;
typedef long long ll;
typedef unsigned int ui;
typedef pair<int,int> Pii;
typedef vector<int> Vi;
template<class T> inline void read(T &x){
x=0; char c=getchar(); int f=1;
while (!isdigit(c)) {if (c=='-') f=-1; c=getchar();}
while (isdigit(c)) {x=x*10+c-'0'; c=getchar();} x*=f;
}
template<class T> T gcd(T a, T b){return !b?a:gcd(b,a%b);}
template<class T> inline void umin(T &x, T y){x=x<y?x:y;}
template<class T> inline void umax(T &x, T y){x=x>y?x:y;}
inline ui R() {
static ui seed=416;
return seed^=seed>>5,seed^=seed<<17,seed^=seed>>13;
}
const int N = 1e5+11;
int n,v[N];
struct line{int a,b,c;}s[N];
bool cmp(const line&x,const line&y){
if(1ll*x.a*y.b!=1ll*x.b*y.a)return 1.0*x.a/x.b<1.0*y.a/y.b;
return 1.0*x.c/x.b<1.0*y.c/y.b;
}
pair<double,int>f[N];
int qry(int p){int r=0;while(p)r+=v[p],p-=p&-p;return r;}
void mdy(int p){while(p<=n)v[p]++,p+=p&-p;}
double solve(){
sort(s+1,s+n+1,cmp);
double l=-2e8,r=2e8;
rep(t,1,85){
double mid=(l+r)/2;
rep(i,1,n)f[i]=mp((s[i].c-mid*s[i].a)/s[i].b,i);
sort(f+1,f+n+1);
rep(i,1,n)v[i]=0;ll res=0;
rep(i,1,n)res+=i-1-qry(f[i].se),mdy(f[i].se);
if(res*2<n*(n-1ll)/2)l=mid;else r=mid;
}
return l;
}
int main() {
read(n);
rep(i,1,n)read(s[i].a),read(s[i].b),read(s[i].c);
printf("%.6lf ",solve());
rep(i,1,n)swap(s[i].a,s[i].b);
printf("%.6lf\n",solve());
return 0;
}


