S2考前综合刷题营Day5

blocks

Description

小明是一个积木爱好者，这一天，小明堆了一堆高度连续递减的积木，假设第 \(i\) 个位置的积木高度为 \(d_i\)， 热爱思考的小明在想，如果每天在第 \(i\) 堆的积木上多加 \(i\) 个，即每天第i堆的积木高度加\(i\)，最短多少天能够出现两堆积木高度相等呢？

小明试了很久也没有达到出现两堆积木高度相等的那天，于是他想找你帮忙计算一下。

Input

第一行一个数 \(n\)，\(n\) 堆积木的原始高度。

接下来一行，\(n\) 个数，第 \(i\) 个数 \(d_i\)，表示第 \(i\) 堆积木的高度。

Output

一个数，即两堆积木相等至少需要的天数。

Sample Input1

5
37 29 24 17 9

Sample Output1

5

Sample Input2

20
569 546 511 472 443 419 388 363 324 286 258 230 209 187 154 129 100 74 53 28

Sample Output2

21

Data

\(40 \%, n ≤ 100，d_i ≤ 10000\)

\(70 \%, n ≤ 5000，d_i ≤ 10^9\)
\(100 \%, n ≤ 100000，d_i ≤ 10^9\)

Solution

70pts

\(O(n^2 )\) 处理，枚举两堆积木 \(i,j\)，计算 \(j\) 追上 \(i\) 至少需要多少天，取最小值即可。

100pts

分析题目性质，发现 \(i\) 每天只比 \(i - 1\) 多加 \(1\)，只比 \(i - 2\) 多加 \(2\)，也就意味着在 \(i\) 要追上 \(i - 2\)，相当于 \(i\)每天花 \(1\) 的价值，追上 \(i - 1\)，同时在 \(i - 1\) 和 \(i - 2\) 的差距上花 \(1\) 的价值追 \(i - 2\)，即花费的时间比 \(\min(i\)追\(i - 1\)的时间，\(i - 1\)追\(i - 2)\) 的时间要长，也就意味着答案为相邻两天差距的最小值。
以我的理解：
由于积木是单调递减的，我们设第 \(i-1\) 堆比第 \(i\) 堆高 \(a\)，第 \(i\) 堆比第 \(i+1\) 堆高 \(b\)，不妨设 \(a>=b\)。
考虑是让相邻的后一个追上前一个的高度，则需要 \(\min(a,b)=b\) 的时间；如果考虑让第 \(i+1\) 堆追上第 \(i-1\) 堆，则需要花 \(\frac{a+b}{2}\) 的时间。
由于 \(a>=b\)，则 \(\frac{a+b}{2}>=\frac{2b}{2}>=b\)，也就是说，此时所花的时间是大于等于让相邻的后一个追上前一个所花的时间。
所以说让后一个追上前一个更优，答案就是相邻的后者减前者再取 \(\min\)。

#include<iostream>
#include<cstdio>
using namespace std;
const int N=1e6;
int n,ans=2e9;
int a[N];
int main()
{
	scanf("%d%d",&n,&a[1]);
	if(n==1)
	{
		printf("0\n");
		return 0;
	}
	for(int i=2;i<=n;i++)
	{
		scanf("%d",&a[i]);
		ans=min(ans,a[i-1]-a[i]);
	}
	printf("%d\n",ans);
	return 0;
}

sort

Description

小明现在手上有一个长度为 \(n\)（\(n\) 为偶数）的序列，序列的值互不相等，但小明觉得一个无序的序列怎也么不好看，于是他想对这个序列进行排序。

小明是一个懒且随便的人，所以对于这个序列的排序，小明觉得其实差不多就行了， 也就是说，如果前 \(\frac{n}{2}\) 个元素里的最大值小于等于后 \(\frac{n}{2}\) 个元素里的最小值，那么小明就觉得这是一个"有序"的序列。

对于每次交换，选择两个不同的序号 \(i\) 和 \(j\) 并交换 \(a_i\) 与 \(a_j\)，每次操作的代价是 \(|i−j|\)。 现在小明想知道对于给定序列转换为一个“有序“的序列所需的最小代价。

Input

第一行一个整数 \(n\)（\(n\) 为偶数），表示序列的长度

接下来一行 \(n\) 个数，描述小明的序列

Output

一个数，即转化为小明认为的有序需要的最小代价

Sample Input

10
39 49 8 16 31 12 22 40 53 58

Sample Output

10

Data

\(40 \%, n ≤ 10\)

\(80 \%, n ≤ 100000\)

\(100 \%, n ≤ 500000，a_i≤10^9\)

Solution

40pts

指数级别大爆搜。

80pts

将序列分为两个部分，前一半和后一半，我们发现需要做的即将前一半排在 \(\frac{n}{2}\) 名后的和后一半排在 \(\frac{n}{2}\) 前的交换位置即可。 仔细分析，发现在哈密尔顿距离下，任意交换花费的值相同，答案即为后一半排在 \(\frac{n}{2}\) 前的位置和减去前一半排在 \(\frac{n}{2}\) 名后的位置和。

100pts

对数值分析，发现答案会超过 \(int\) 范围，开 \(long long\) （提醒一下，\(noip\) 争取不要再出现同样的错误）

#include<algorithm>
#include<iostream>
#include<cstdio>
using namespace std;
const int N=1e6;
int n,a[N],b[N];
long long ans;
bool cmp(int x,int y)
{
	return x<y;
}
int main()
{
	freopen("T2.in","r",stdin);
	scanf("%d",&n);
	for(int i=1;i<=n;i++) 
	{
		scanf("%d",&a[i]);
		b[i]=a[i];
	}
	sort(b+1,b+1+n,cmp);
	for(int i=1;i<=n/2;i++)
	{
		if(a[i]>=b[n/2+1]) ans-=i;
	}
	for(int i=n/2+1;i<=n;i++)
	{
		if(a[i]<=b[n/2]) ans+=i;
	}
	printf("%lld\n",ans);
	return 0;
}

string

Description

李华给了小明一堆字符串,所有字符串由 '\(a\)' 到 '\(z\)' 组成，小明还是觉得一堆串太乱了，为了美观，小明决定给所有串分个类。

具体地，小明现在有了 \(n\) 个字符串，想要划分到 \(\frac{n}{k}\) 个集合中，每个集合共 \(k\) 个字符串，为了使每个集合尽可能整齐，小明定义一个集合的美观度为该集合中所有字符串公共前缀的长度，

即假设集合为 "\(noipac,noipak,noipcspak\)"，可知他们有公共前缀 "\(noip\)"，即集合的美观度为 \(4\)。

现在，小明想知道对于划分后的 \(\frac{n}{k}\) 个集合，美观度之和最大是多少。

Input

第一行两个正整数 \(n,k\)，分别表示字符串总数和每个集合的字符串数量

接下来 \(n\) 行，每行一个字符串

Output

一个数，即美观度之和最大是多少

Sample Input

6 2
noipac
noipak
noipcspac
cspac
cspak
noipcspak

Sample Output

17

Data

\(40 \%, n ≤ 10,k ≤ 5,\)每个字符串长度 \(≤ 100\)

\(70 \%, n ≤ 10000,K ≤ n,\)每个字符串长度 \(≤ 100\)

\(100 \%, n ≤ 100000,K ≤ n,\)每个字符串长度 \(≤ 100000,\)字符串总长度不超过 \(2∗10^6\)，\(k\) 整除 \(n\)。

Solution

30pts

指数级别大爆搜，枚举每个串在哪个集合，并计算公共前缀长度。

60pts

在无序的情况下思考比较困难，由于问题与顺序无关，不妨从考虑从有序的角度思考。
排序后，发现前缀存在一个性质，即 \(i\) 和 \(i + 2\) 的公共前缀长度 \(= \min(i\) 和 \(i + 1\) 的公共前缀，\(i+1\) 和 \(i+2\) 的公共前缀),也就意味着，假设现在剩余 \(n\) 串，将 \(n\) 个串排序后看做一个环形，其中包含第 \(1\) 个串的集合，为环形上连续的一块，采用区间动态规划处理。
\(f[i][j]\) 表示区间剩余 \([i,j]\) 的最大美观度，\(O(k)\) 枚举第 \(i\) 串和哪一串合并在一起，并转移。
时间复杂度 \(O(n^2)\)。

100pts

对于有关字符串前缀的问题，我们可以在 \(Trie\) 树上解决。
我们可以在插入字符串的过程中维护一个数组：\(size[i]\) 表示 \(Trie\) 中编号为 \(i\) 的子树中有多少个字符串的结束标志。
维护的话我们可以在插入的过程中把经过的节点的 \(size++\) 就好了。
现在考虑这个东西能干什么。
如果一个节点 \(u\) 的 \(size\) 是大于等于 \(K\) 的，且它的所有儿子的 \(size\) 都是小于 \(K\) 的，那么说明 \(u\) 的子树中的字符串的最长公共前缀就是从根节点一直到 \(u\) 路径上所对应的字符。
比如我们现在有两个字符串 \(noip\) 和 \(noia\)，\(K=2\)：

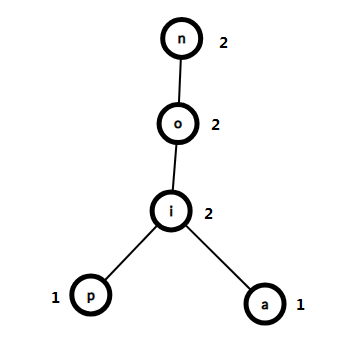
由于 \(i\) 这个节点的 \(size>=2\)，且它的儿子 \(p\) 和 \(a\) 的 \(size\) 都 \(<2\)，所以这两个字符串的最长公共前缀一定是从根节点 \(n\) 一直到 \(i\) 的路径：\(noi\)。
所以在求答案的时候我们可以 \(dfs\) 遍历每个点，让字符串在最优的情况（上面讨论的情况）进行分组即可。

#include<iostream>
#include<string>
#include<cstdio>
using namespace std;
const int N=5e5+5;
int n,k,cnt=1,c[N][30],dep[N*30],size[N*30];
string S;
long long ans;
void insert(string s)
{
	int u=1;
	for(int i=0;i<s.size();i++)
	{
		dep[u]=i;               //维护每个点的深度 
		int ch=s[i]-'a';
		if(!c[u][ch]) c[u][ch]=++cnt;
        size[u]++;u=c[u][ch];   //维护size    
	}
	size[u]++;dep[u]=s.size();
}
void dfs(int u)
{
	if(size[u]<k) return ;      //如果这个点内的结束标记小于K个,是不能进行分组的 
	for(int i=0;i<26;i++)
	{
		int v=c[u][i];
		if(v) size[u]-=(size[v]/k)*k,dfs(v);	//由于字符串可能会在v中分组,所以这里要减点已经分了组的字符串的size 
	}
	ans+=(size[u]/k)*dep[u];    //如果还余下几个字符串没有分组,那么现在能分组就分吧,因为更优的情况已经考虑过了 
	size[u]-=(size[u]/k)*k;
}
int main()
{
	scanf("%d%d",&n,&k);
	for(int i=1;i<=n;i++)
		cin>>S,insert(S);       //把每个字符串插入到trie中 
	dfs(1);printf("%lld\n",ans);
	return 0;
}

dinner

Description

小明所在的班级要组织一个聚餐，已知班级里一共 \(n\) 名同学，编号为 \(1\) 到 \(n\)，其中有 \(m\) 对同学关系不好，如果同时在一起就会相互卷起来。

在聚餐时卷起来是大家都不想看到的事情，为此，小明提出了 \(q\) 种方案，第 \(i\) 种方案由 \([L_i,R_i]\) 区间组成，表示本次聚餐由所有区间内的同学共同参加。

然而，其实小明自己也不知道每个方案里面，会不会有一对关系不好的人卷起来，为此他找到了你来帮忙。

Input

第一行；三个正整数 \(n,m,q\)，分别表示班级同学总数和关系不好的同学对数，以及方案个数。

接下来 \(m\) 行，每行两个数 \(u,v\)，表示 \(u,v\) 关系不太好，同一个同学可能与多个同学关系不好。

接下来 \(q\) 行，每行首先一个数 \(k\)，表示区间个数，接下来 \(2 * k\) 个数，描述 \(L_1,R_1...L_k,R_k\)。

Output

\(q\) 行，对于每个方案，回答 "GG" 表示会有人卷起来，"SAFE"表示没有关系不好的同学同时在场。

Sample Input

10 5 3
3 8
3 2
8 4
8 5
5 8
2 1 3 6 8
1 3 5
2 4 6 9 10

Sample Output

GG
SAFE
SAFE

Data

\(40 \%, n,m,Q ≤ 1000,K ≤ 100\)

\(80 \%, n,m,Q ≤ 200000,K ≤ 100,\sum{k}≤200000\)
\(100 \%, n,m,Q ≤ 200000,K ≤ n,\sum{k}≤200000\)

Solution

40pts

对于每一个方案，将方案提出的区间标为 \(1\)，再枚举每一对关系不好的同学，判断是否同时为 \(1\)，时间复杂度 \(O(Q * (n + m))\)。
但是清北神机能让你拿到 \(100pts\) 的好成绩。

80pts

\(k\) 比较小，考虑设计一个与 \(k\) 相关的算法，离线处理 \(+\) 线段树维护，考虑关系不好的对 \([i,j]\)，\(i ≤j\)，从 \(1\) 到 \(n\) 枚举每一个同学，枚举到 \(j\) 时，将与 \(j\) 关系不好的位置 \(i\) 在线段树中的值设为 \(j\)，如果 \(j\) 为某个方案中某个区间 \([x,j]\) 的右端点，即我们在线段树中查找该方案中，该区间前的区间最大值，如果存在某个区间最大值大于 \(x\)，则该方案存在冲突，对于每个方案，假设有 \(k_i\) 个区间，则需要查询 \({k_i}^2\) 次，总复杂度 \(O(m\log{n} +\sum{k^2}\log{n})\)。

100pts

做法一：
考虑通过差分\(+\)位运算压位来解决问题。考虑暴力"将方案提出的区间标为\(1\)"，即差分后将两个区间端点左端点加 \(1\)，右端点 \(+1\) 位置减 \(1\)，随后，通过前缀和，我们可以得到整个区间的每个位置
的表示，发现一个 \(int\) 数值只置为 \(1\) 是非常浪费的，可以考虑位运算压位，\(long long\) \(60\) 位每一位处理一个方案。
时间复杂度 \(O(Q * \frac{n + m}{60})\)。
做法二：
考虑分块处理。将 \(40\) 分做法和 \(80\) 分做法结合起来，当 \(k ≥ lim\) 时，采用 \(40\) 分做法，当 \(k < lim\) 时采用 \(80\) 分做法。
时间复杂度 \(O((n + m) * \frac{Q}{lim} + (n + m)\log{n} + Q * lim * \log{n})\)。
做法一的 \(code:\)

#include<iostream>
#include<cstring>
#include<cstdio>
#define ll long long
using namespace std;
inline int read()
{
	char ch=getchar();
	int a=0,x=1;
	while(ch<'0'||ch>'9') ch=getchar();
	while(ch>='0'&&ch<='9') a=(a<<1)+(a<<3)+(ch^48),ch=getchar();
	return a;
}
const int N=1e6;
const int lim=60;
int n,m,q,cnt;
ll bits[N];                
bool ans[N];
struct node
{
	int l,r;
}a[N];
void solve()               //处理每个方案是否合法 
{
	ll sum=0;              //sum的二进制第i位表示第i个方案是否合法 
	for(int i=1;i<=n;i++) bits[i]+=bits[i-1];   //通过前缀和得到每个位置的准确值 
	for(int i=1;i<=m;i++) sum|=(bits[a[i].l]&bits[a[i].r]);  //枚举m个矛盾关系,如果两者都在方案里,那就是矛盾的 
	for(int i=0;i<lim;i++) ans[++cnt]=sum&(1ll<<i); //cnt表示当前处理到第几个方案数了 
	return ;
}
int main()
{
	n=read();m=read();q=read();
	for(int i=1;i<=m;i++) a[i].l=read(),a[i].r=read();  //存所有矛盾关系 
	int L1,R1,L2,R2,K;
	for(int i=0;i<q;i++)
	{
		int id=i%lim;       //我们把每60个压成一组 
		if(id==0) memset(bits,0,sizeof(bits));	//这是新的一组 
		K=read();L1=read();R1=read();   //[L1,R1]表示上一个区间,[L2,R2]表示当前区间 
		for(int j=1;j<K;j++)
		{
			L2=read();R2=read();
			if(L2==R1)      //如果当前区间能和上一个区间合并起来,那就合并   
			{
				R1=R2;
				continue;
			}
			else            //否则利用差分,将上一个区间的左端点的位置+1,右端点加一的位置-1 
			{
 				bits[L1]+=1ll<<id;   //注意要把第id位的加上一,表示第id个方案 
				bits[R1+1]-=1ll<<id;
				L1=L2;R1=R2;
			}
		}
		bits[L1]+=1ll<<id;  //别忘了处理最后一个区间 
		bits[R1+1]-=1ll<<id;
		if(id==lim-1) solve();  //如果这个方案是当前组的最后一个了(第60个了),我们处理一下答案 
	}
	if(q%lim!=0) solve();   //如果还有余的方案,也别忘了处理 
	for(int i=1;i<=q;i++)   //输出每个方案是否合法 
	{
		if(ans[i]) printf("GG\n");
		else printf("SAFE\n");
	}
	return 0;
}