P2303 [SDOI2012] Longge 的问题

好久没做数学题了，看到这个题我顿时傻了。

题解

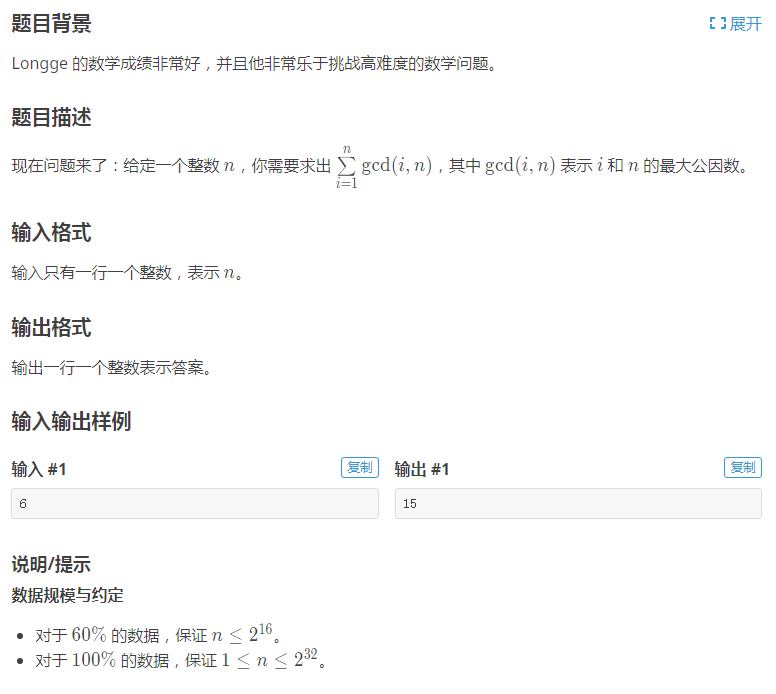
首先我们看到题目中我们要求的式子：\(\sum_{i=1}^{n}gcd(i,n)\)。
试想一下，如果有个 \(i\) 使得 \(gcd(i,n)=d\)，那么这个 \(i\) 的贡献就是 \(d\)，所以有多少个这样的 \(i\) 就会贡献出多少个 \(d\)。
\(d\) 一定是 \(n\) 的因子。
那怎么求有多少个这样的 \(i\) 呢？
我们将 \(gcd(i,n)=d\) 进一步化简： \(gcd(\frac{i}{d},\frac{n}{d})=1\)。
这一步转化之后，答案就很明显了：
我们要求有多少个 \(i\) 使得 \(gcd(i,n)=d\)，可以转化为求有多少个 \(\frac{i}{d}\) 使得 \(gcd(\frac{i}{d},\frac{n}{d})=1\)，即求多少个数与 \(\frac{n}{d}\) 互质。
这里引入欧拉函数。

欧拉函数

定义：在数论，对正整数 \(n\)，欧拉函数是小于或等于 \(n\) 的正整数中与 \(n\) 互质的数的数目（因此 \(φ(1)=1\)）。
通式：若 \(n=p_1^{q_1}p_2^{q_2}p_3^{q_3}...p_k^{q_k}(p_1,p_2...p_k\)均为质数\()\)，则 \(φ(n)=n*(1-\frac{1}{p_1})*(1-\frac{1}{p_2})*(1-\frac{1}{p_3})...*(1-\frac{1}{p_k})\)。
若 \(n\) 为质数，则 \(φ(n)=n-1\)。
性质：
\(①.\)若 \(m,n\) 互质，则 \(φ(m*n)=φ(m)*φ(n)\)。
\(②.\)若 \(p\) 是 \(n\) 的质因子，则 \(φ(n*p)=p*φ(n)\)。
\(③.\)若 \(n\) 为奇质数，则 \(φ(2n)=φ(n)\)。
代码实现：
我们将通式变形一下下：\(φ(n)=n*\frac{p_1-1}{p_1}*\frac{p_2-1}{p_2}*\frac{p_3-1}{p_3}...*\frac{p_k-1}{p_k}\)。
我们可以枚举 \(n\) 的每个质因子 \(p_i\)，然后将答案乘 \(\frac{p_i-1}{p_i}\)，然后再把 \(n\) 中的质因子 \(p_i\) 全部除掉。

ll phi(ll x)               //求φ(n) 
{
	ll cnt=x;
	for(ll i=2;i*i<=x;i++) //枚举x的质因子 
	{
		if(x%i==0)         //由于每个合数也可以由质数表示,所以i只能是质因子 
		{
			cnt=cnt/i*(i-1); //统计答案 
			while(x%i==0) x/=i; //将x中的i全部除掉,这样才能保证枚举到全是质因子 
		}
	}
	if(x>1) cnt=cnt/x*(x-1); //如果x>1,说明还有个质因子没有统计到,我们在这里将其统计上 
	return cnt;
}

回到题目

介绍完欧拉函数，本题的解法就出来了。
我们枚举 \(n\) 的因子 \(d\)，然后求有多少个 \(i\) 的贡献是 \(d\)，个数为 \(φ(\frac{n}{d})\)，那么总贡献就是 \(\sum_{d|n}d*φ(\frac{n}{d})\)。
\(Code:\)

#include<iostream>
#include<cstdio> 
#define ll long long
using namespace std;
const int N=1005;
ll n,ans;
ll phi(ll x)               //求φ(n) 
{
	ll cnt=x;
	for(ll i=2;i*i<=x;i++) //枚举x的质因子 
	{
		if(x%i==0)         //由于每个合数也可以由质数表示,所以i只能是质因子 
		{
			cnt=cnt/i*(i-1); //统计答案 
			while(x%i==0) x/=i; //将x中的i全部除掉,这样才能保证枚举到全是质因子 
		}
	}
	if(x>1) cnt=cnt/x*(x-1); //如果x>1,说明还有个质因子没有统计到,我们在这里将其统计上 
	return cnt;
}
int main()
{
	scanf("%lld",&n);
	for(ll i=1;i*i<=n;i++)   //枚举n的因子 
	{
		if(n%i==0)           
		{
			ans+=phi(n/i)*i; //算贡献 
			if(i*i!=n) ans+=phi(i)*(n/i);  //如果i是n的因子,那么n/i也是n的因子,我们再算上n/i的贡献 
		}
	}
	printf("%lld\n",ans);
	return 0;
}