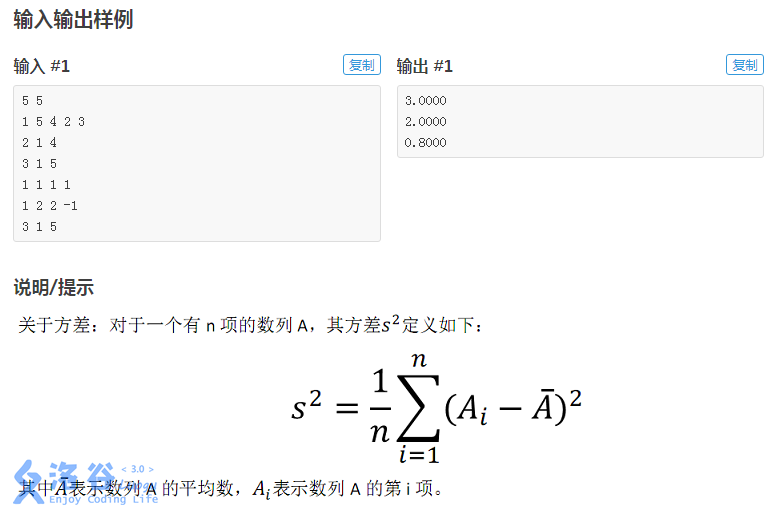
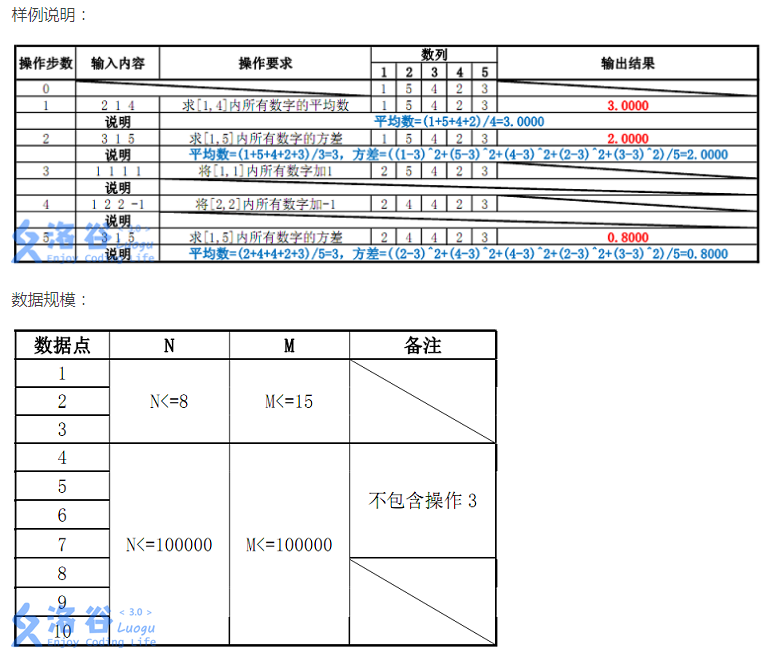
P1471 方差

原题链接  https://www.luogu.com.cn/problem/P1471

 

 

 

 

题解

我们先对题目中给出的求方差的式子进行化简：

 

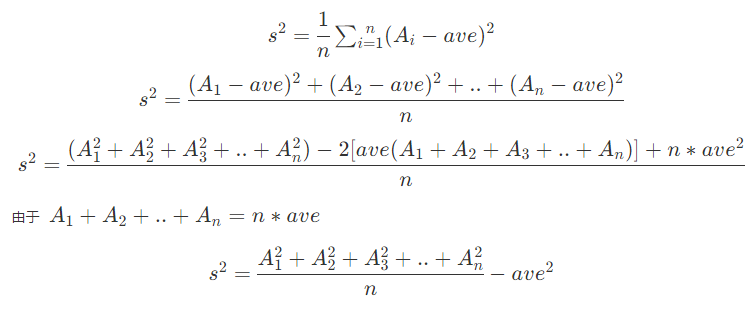
我们需要维护区间和和区间平方和，因为平均数可以通过区间和得到；

看一下区间加 k 后方差有什么变化：

 

可以看到维护平方和的时候是要用到区间和的，所以我们应该先维护平方和再维护区间和。

还有就是注意要用 double ！

Code：

#include<iostream>
#include<cstdio>
using namespace std;
int read()
{
    int a=0,x=1;
    char ch=getchar();
    while(ch<'0'||ch>'9')
    {
        if(ch=='-') x=-x;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        a=(a<<1)+(a<<3)+(ch-'0');
        ch=getchar();
    } 
    return a*x;
}
const int N=100005;
int n,m,oper;
double k,a[N],sum[N<<2],tag[N<<2],pfh[N<<2];   //sum:区间内所有数的和;pfh:区间内所有数的平方和 
void pushup(int node)                          //上传 
{
    sum[node]=sum[node<<1]+sum[node<<1|1];
    pfh[node]=pfh[node<<1]+pfh[node<<1|1];
}
void pushdown(int node,int l,int r)            //下传懒标记 
{
    int mid=(l+r)/2;
    double k=tag[node];
    pfh[node<<1]+=(mid-l+1)*k*k+2.0*k*sum[node<<1];     //注意平方和的优先级要更高 
    pfh[node<<1|1]+=(r-mid)*k*k+2.0*k*sum[node<<1|1];
    sum[node<<1]+=(mid-l+1)*k;                          //其次再算区间和 
    sum[node<<1|1]+=(r-mid)*k;
    tag[node<<1]+=k;
    tag[node<<1|1]+=k;
    tag[node]=0;
}
void build(int node,int l,int r)                //建树 
{
    if(l==r) 
    {
        sum[node]=a[l];
        pfh[node]=a[l]*a[l];
        return ;
    }
    int mid=(l+r)/2;
    build(node<<1,l,mid);
    build(node<<1|1,mid+1,r);
    pushup(node);
}
void add(int node,int l,int r,int x,int y,double k)
{
    if(x<=l&&r<=y)
    {
        pfh[node]+=(r-l+1)*k*k+2.0*k*sum[node];  //区间加k之后平方和的变化 
        sum[node]+=(r-l+1)*k; 
        tag[node]+=k;
        return ;
    }
    pushdown(node,l,r);
    int mid=(l+r)/2;
    if(x<=mid) add(node<<1,l,mid,x,y,k);
    if(y>mid) add(node<<1|1,mid+1,r,x,y,k);
    pushup(node);
}
double ask1(int node,int l,int r,int x,int y)    //询问区间和 
{
    if(x<=l&&r<=y) return sum[node];
    pushdown(node,l,r);
    int mid=(l+r)/2;
    double cnt=0;
    if(x<=mid) cnt+=ask1(node<<1,l,mid,x,y);
    if(y>mid) cnt+=ask1(node<<1|1,mid+1,r,x,y);
    return cnt;
}
double ask2(int node,int l,int r,int x,int y)    //询问区间平方和 
{
    if(x<=l&&r<=y) return pfh[node];
    pushdown(node,l,r);
    int mid=(l+r)/2;
    double cnt=0;
    if(x<=mid) cnt+=ask2(node<<1,l,mid,x,y);
    if(y>mid) cnt+=ask2(node<<1|1,mid+1,r,x,y);
    return cnt;
}
int main()
{
    n=read();m=read();
    for(int i=1;i<=n;i++) scanf("%lf",&a[i]);
    build(1,1,n);
    for(int i=1;i<=m;i++)
    {
        int x,y;
        oper=read();
        x=read();y=read();
        if(oper==1)
        {
            scanf("%lf",&k);
            add(1,1,n,x,y,k);     //区间[x,y]加上k 
        }
        if(oper==2)               
        {
            printf("%.4lf\n",ask1(1,1,n,x,y)/(y-x+1));  //询问[x,y]的平均数 
        }
        if(oper==3)
        {
            double a,b,c;
            a=ask2(1,1,n,x,y);    //区间平方和 
            c=(double)y-x+1;      //区间长度 
            b=ask1(1,1,n,x,y)/c;  //区间平均数          
            printf("%.4lf\n",a/c-b*b);   //询问[x,y]的方差 
        }
    }
    return 0;
}