P1379 八数码难题

原题链接  https://www.luogu.com.cn/problem/P1379

 

 

题解 

八数码难题，一道十分经典的 $bfs$ 搜索题，所以我们可以用 $bfs$ 来解决这道题；

一. 单向 $bfs$

我们可以将这九个格子依次排成一排，这样一个 $3*3$ 的矩阵就可以转化为一个九位数的数字，这样可以方便我们保存状态；

每走一步就是将 $0$ 上下左右四个方向的数字移到 $0$ 的位置，这样那个数字的位置就空了，就变成了 $0$，那么每走一步就可以看做是将 $0$ 与四周的数字交换的过程；

从初始状态进行 $bfs$ ，每转移一个新状态就压入队列里，同时记录初始状态到这个新状态的步数，过程中注意判重，直到扩展到目标布局；

二. 双向 $bfs$

由于单向 $bfs$ 的时间复杂度忒高，我们可以考虑双向 $bfs$ ；

双向 $bfs$ 适用于知道起点和终点的状态下使用，从起点和终点两个方向开始进行搜索，可以非常大地提高单个 $bfs$ 的搜索效率；
同样，实现也是通过队列的方式，可以设置两个队列，一个队列保存从起点开始搜索的状态，另一个队列用来保存从终点开始搜索的状态，如果某一个状态下出现相交的情况，那么就出现了答案；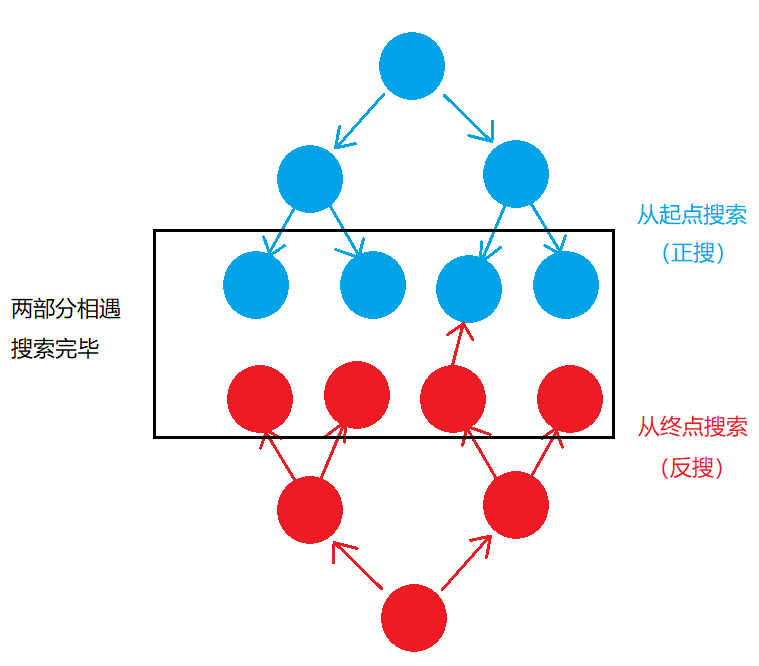

 

 思路和单向 $bfs$ 的一样，需要注意的地方代码里详细地注释了哦~

$Code$：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<map>
#include<queue>
using namespace std;
int read()
{
    char ch=getchar();
    int a=0,x=1;
    while(ch<'0'||ch>'9')
    {
        if(ch=='-') x=-x;
        ch=getchar(); 
    }
    while(ch>='0'&&ch<='9')
    {
        a=(a<<1)+(a<<3)+(ch-'0');
        ch=getchar(); 
    }
    return a*x;
}
const int E=123804765;
int S,x,y,Ans;
int a[4][4],dx[4]={0,0,1,-1},dy[4]={1,-1,0,0};
map<int,int> ans;     //表示搜索到当前状态需要多少步 
map<int,int> state;   //表示每种状态是正搜得到还是反搜得到 
queue<int> q;
void work1(int A)     //数字转化为矩阵 
{
    int w=100000000;
    for(int i=1;i<=3;i++)
    {
        for(int j=1;j<=3;j++)
        {
            a[i][j]=(A/w)%10;
            if(a[i][j]==0) x=i,y=j;
            w/=10;
        }
    }
}
int work2()           //将矩阵转化为数字              
{
    int now=0;
    for(int i=1;i<=3;i++)
    {
        for(int j=1;j<=3;j++)
        {
            now=now*10+a[i][j];
        }
    }
    return now;
}
void bfs()
{
    if(S==E) return ; //这里要特判一下,不然会TLE            
    state[S]=1;       //用1表示当前状态是正搜得到 
    state[E]=2;       //用2表示当前状态是反搜得到 
    ans[S]=0;         //初始状态不用搜索即可得到 
    ans[E]=0;         //最终状态不用搜索即可得到 
    q.push(S);        //这里将正搜反搜的两个队列压成一个,节省空间 
    q.push(E);
    while(!q.empty())
    {
        int now,cur;
        now=cur=q.front();  //cur表示即将要被扩展的状态 
        q.pop();
        work1(now);   //将数字转化为矩阵，并找出0的坐标 
        for(int i=0;i<4;i++)//向四种方向扩展(将0与四周的数字进行交换) 
        {
            int nx=x+dx[i];
            int ny=y+dy[i];
            if(nx<1||nx>3||ny<1||ny>3) continue;  //出界的情况不考虑 
            swap(a[x][y],a[nx][ny]);    //交换得到新状态 
            now=work2();                //将新状态转化成数字 
            if(state[now]==state[cur])  //如果新状态和当前状态同时被一种搜索(正搜或反搜一种)搜到了,说明这个状态已经搜过了不用再搜了 
            {
                swap(a[x][y],a[nx][ny]);//此时九宫格的状态还是新状态，注意要换回来 
                continue;
            } 
            if(state[now]+state[cur]==3)//如果新状态和当前状态分别被正搜和反搜搜到(1+2=3)，那么就搜完了 
            {
                Ans=ans[now]+ans[cur]+1;//注意要考虑上当前状态转移到新状态的步数，所以别忘了加一 
                return ;
            }
            ans[now]=ans[cur]+1;        //转移步数 
            state[now]=state[cur];      //新状态由当前状态转移而来，那么它们一定被同一种搜索搜到 
            q.push(now);                //新状态入队，继续进行扩展 
            swap(a[x][y],a[nx][ny]);    //这里别忘了换回当前状态 
        }
    }
}
int main()
{
    S=read();                           //输入初始状态     
    bfs();                              //双向bfs 
    printf("%d\n",Ans);                 //输出答案 
    return 0;
}

 

萌新也是初探双向 $bfs$，如果您有任何疑问可以在评论区留言哦，我尽量一一解答，感谢您们的观看$qwq$。