2019.11.11 模拟赛 T2 乘积求和

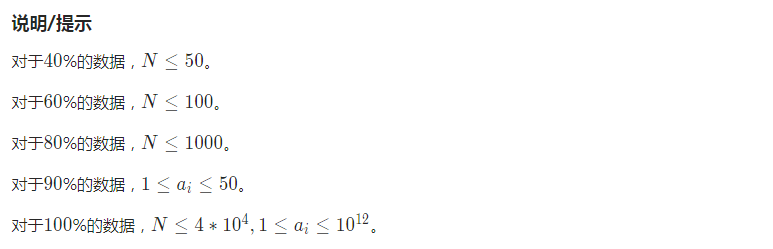
昨天 ych 的膜你赛,这道题我 O ( n4 ) 暴力拿了 60 pts。
这道题的做法还挺妙的,我搞了将近一天呢qwq
题解
60 pts
根据题目给出的式子,四层 for 循环暴力枚举统计答案即可;
#include<iostream> #include<cstdio> using namespace std; int read() { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } const long long mod=1e12+7; int n; long long ans,a[100000]; int main() { freopen("multiplication.in","r",stdin); freopen("multiplication.out","w",stdout); n=read(); for(int i=1;i<=n;i++) a[i]=read(); for(int l=1;l<=n;l++) for(int r=l;r<=n;r++) for(int i=l;i<=r;i++) for(int j=i+1;j<=r;j++) if(a[i]>a[j]) ans=(ans+a[i]*a[j]%mod)%mod; printf("%lld\n",ans); return 0; }
80 pts
方法一:预处理 + O ( n2 )
我们可以翻译一下题目中给出的式子:
就是求所有区间中每个区间的逆序对乘积;
那么我们可以提前预处理出每个区间的答案,再统计答案;
时间复杂的 O ( n2 ),期望得分 80 pts;
for(int i=1;i<=n;i++) { for(int j=i;j<=n;j++) { f[i][j]=f[i][j-1]; if(a[j]<a[i]) f[i][j]=(f[i][j]+a[i]*a[j]%mod)%mod; } } for(int i=1;i<=n;i++) { for(int j=i+1;j<=n;j++) { ans=(ans+i*f[i][j])%mod; } }
方法二:归并排序
考虑一对逆序对 ( ai , aj ) 会在所有的区间内出现几次 。
因为同时包含 ai 和 aj 的最小区间是 [ i , j ],所以左端点小于等于 i,右端点大于等于 j 的所有区间也包含,所有共有 i * ( n - j + 1 );
所以我们可以去找出所有的逆序对,然后去计算他们对答案的贡献;
求逆序对,我们可以用归并排序;
具体思路就是在两部分合并的过程中,如果左半部分的某个数 ai 大于右半部分某个数 aj ,这时候从 ai ~ amid 都会与 aj 产生一组逆序对,我们统计答案就好了;
#include<iostream> #include<cstdio> using namespace std; long long read() { char ch=getchar(); long long a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } const long long mod=1e12+7; const int N=5e4; long long n,ans; struct node { long long val,id; }a[N],c[N]; void gb_sort(int l,int r) { if(l==r) return ; int mid=(l+r)>>1; gb_sort(l,mid); gb_sort(mid+1,r); int i=l,j=mid+1; int k=l-1; while(i<=mid&&j<=r) { if(a[i].val>a[j].val) { for(int l=i;l<=mid;l++) ans=(ans+a[l].val*a[j].val%mod*a[l].id*(n-a[j].id+1)%mod)%mod; //printf("%lld\n",ans); c[++k].val=a[j].val;c[k].id=a[j].id; j++; } else { c[++k].val=a[i].val;c[k].id=a[i].id; i++; } } while(i<=mid) { c[++k].val=a[i].val;c[k].id=a[i].id; i++; } while(j<=r) { c[++k].val=a[j].val;c[k].id=a[j].id; j++; } for(int i=l;i<=r;i++) { a[i].id=c[i].id; a[i].val=c[i].val; } } int main() { freopen("multiplication.in","r",stdin); freopen("multiplication.out","w",stdout); n=read(); for(int i=1;i<=n;i++) { a[i].val=read(); a[i].id=i; } gb_sort(1,n); printf("%lld\n",ans); return 0; }
90 pts
发现正是归并排序统计答案的时候是 O ( n ) 的,使得复杂度升高了;
我们想能不能优化下:
还是按照上面的思路,如果在合并的时候有 ai > aj ,则 ai ~ amid 都会与 aj 产生逆序对,那么 aj 产生的贡献之和就是:
ai * aj * i * ( n - j + 1 ) + ai+1 * aj * ( i+1 ) * ( n - j + 1 ) + …… + amid * aj * mid * ( n - j + 1 )
我们将 aj * ( n - j + 1 ) 提出来就是:
aj * ( n - j + 1 ) * [ ai * i + ai+1 * ( i+1 ) + ai+2 * ( i+2 ) + amid * mid ]
也就是说,我们可以统计在 aj 之前的所有数中,每个比 aj 大的数 ai 再乘上 ai 的下标 i 的和是多少,记为 sum;
则 sum = ai * i + ai+1 * ( i+1 ) + ai+2 * ( i+2 ) + amid * mid,那么 aj 对答案的贡献就是:sum * aj * ( n - j + 1 )
然后我们发现这东西可以用权值树状数组来维护:
每个下标为 i 的数组维护 ai * i 的值是多少,当我们对原数列的数依次放到树状数组的时候,由于前面的数已经放进去了,我们可以去统计有所有比当前数大的数(可以与当前数构成逆序对的数)它们的 ai * i 的值的和是多少;由于是权值树状数组,所以比当前数要大的数在树状数组里的编号是比当前数的编号大的,所以我们可以求后缀和;但是由于我们不会求后缀和,所以我们可以把权值树状数组的编号反过来存,大的在前面,小的在后面,这样就转化成了我们熟悉的前缀和啦;
但是由于每个元素的权值范围较大,且逆序对的产生只与两个数的大小关系有关,与两个数具体是多少无关,所以我们可以先离散化;
时间复杂度 O ( nlog n ),期望得分 90 pts;
#include<iostream> #include<cstdio> #include<algorithm> using namespace std; long long read() { char ch=getchar(); long long a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } const long long mod=1e12+7; const long long N=1e5; long long n; long long ans,c[N]; struct node { long long id,val,rank; }a[N]; bool cmp1(node x,node y) { if(x.val!=y.val) return x.val<y.val; return x.id<y.id; } bool cmp2(node x,node y) { return x.id<y.id; } void lsh() //离散化 { sort(a+1,a+1+n,cmp1); //先按照大小排序 for(long long i=1;i<=n;i++) a[i].rank=i; //按大小关系给每个元素分个排名,就是离散化之后的大小 sort(a+1,a+1+n,cmp2); //再按照在原序列里的编号排回去 } long long lowbit(long long x) { return x&(-x); } long long ask(long long x) //树状数组求[1,x]的和 { long long y=0; for(long long i=x;i;i-=lowbit(i)) y=(y+c[i]+mod)%mod; return y; } void add(long long x,long long y) //将第x个数加y { for(long long i=x;i<=n;i+=lowbit(i)) c[i]=(c[i]+y+mod)%mod; } int main() { freopen("multiplication.in","r",stdin); freopen("multiplication.out","w",stdout); n=read(); for(long long i=1;i<=n;i++) { a[i].val=read(); //每个元素的大小 a[i].id=i; //每个元素在原序列里的编号(是第几个) } lsh(); //离散化 for(long long i=1;i<=n;i++) //依次将每个数丢进树状数组 { long long sum=ask(n-a[i].rank+1); //求一次前缀和,注意这里大小编号是反着的 ans=(ans+sum*a[i].val%mod*(n-a[i].id+1)%mod)%mod; //算当前元素对答案的贡献 add(n-a[i].rank+1,a[i].id*a[i].val%mod); //将当前元素丢进树状数组里,维护的是这个数的下标*权值 } printf("%lld\n",ans%mod); return 0; }
100 pts
不是,我时间复杂度 O ( nlog n ) 跑的飞快啊,怎么还没满分?
有一个小细节需要注意:
我们的模数是 1012 +7,两个数相乘很可能爆 long long 的。
这时候我们就要用到龟速乘了qwq:
龟速乘
龟速乘好像就是来弥补快速幂的 bug 的,虽然计算速度真的龟速。。。
它的原理是这样的:
假如我们现在要计算一个简单的式子:3 * 23
然后我们将 23 用二进制表示一下子:( 23 )10 = ( 10111 )2
那么我们可以将 23 写成这个形式:23 = 20 + 21 + 22 + 24
然后我们再将其代回原式:3 * 23 = 3 * ( 20 + 21 + 22 + 24 ) = 3 * 20 + 3 * 21 + 3 * 22 + 3 * 24
然后我们发现每次加的 3 的系数都是原来的两倍,这一点与快速幂类似;
代码实现:
long long slow_pow(long long a,long long b) //龟速乘计算a*b { long long tot=0; while(b) { if(b&1) tot=(tot+a+mod)%mod; a=(a+a+mod)%mod; //每次变为原来的2倍 b>>=1; } return tot; }
然后套上龟速乘,这个题最后的坑就被我们填完了,完整AC代码如下:
#include<iostream> #include<cstdio> #include<algorithm> using namespace std; long long read() { char ch=getchar(); long long a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } const long long mod=1e12+7; const long long N=1e5; long long n; long long ans,c[N]; struct node { long long id,val,rank; }a[N]; long long slow_pow(long long a,long long b) //龟速乘计算a*b { long long tot=0; while(b) { if(b&1) tot=(tot+a+mod)%mod; a=(a+a+mod)%mod; //每次变为原来的2倍 b>>=1; } return tot; } bool cmp1(node x,node y) { if(x.val!=y.val) return x.val<y.val; return x.id<y.id; } bool cmp2(node x,node y) { return x.id<y.id; } void lsh() //离散化 { sort(a+1,a+1+n,cmp1); //先按照大小排序 for(long long i=1;i<=n;i++) a[i].rank=i; //按大小关系给每个元素分个排名,就是离散化之后的大小 sort(a+1,a+1+n,cmp2); //再按照在原序列里的编号排回去 } long long lowbit(long long x) { return x&(-x); } long long ask(long long x) //树状数组求[1,x]的和 { long long y=0; for(long long i=x;i;i-=lowbit(i)) y=(y+c[i]+mod)%mod; return y; } void add(long long x,long long y) //将第x个数加y { for(long long i=x;i<=n;i+=lowbit(i)) c[i]=(c[i]+y+mod)%mod; } int main() { freopen("multiplication.in","r",stdin); freopen("multiplication.out","w",stdout); n=read(); for(long long i=1;i<=n;i++) { a[i].val=read(); //每个元素的大小 a[i].id=i; //每个元素在原序列里的编号(是第几个) } lsh(); //离散化 for(long long i=1;i<=n;i++) //依次将每个数丢进树状数组 { long long sum=ask(n-a[i].rank+1); //求一次前缀和,注意这里大小编号是反着的 ans=(ans+slow_pow(slow_pow(sum,a[i].val)%mod,(n-a[i].id+1))%mod)%mod; //算当前元素对答案的贡献 add(n-a[i].rank+1,slow_pow(a[i].id,a[i].val)%mod); //将当前元素丢进树状数组里,维护的是这个数的下标*权值 } printf("%lld\n",ans%mod); return 0; }
这道题让我重新温习了我不熟悉的数据结构,让我距目标更近了一步呢,最后,CSP 加油!


