P5025 [SNOI2017]炸弹
原题链接 https://www.luogu.org/problem/P5025
闲话时刻:
第一道 AC 的黑题,虽然众人皆说水。。。
其实思路不是很难,代码也不是很难打,是一些我们已经学过的东西凝合在一起,只要基础扎实的话,做出这道题目来说也就很简单了(不包括我);
题目大意:
有 n 个点,每个点可影响到它左右各 R [ i ] 范围内的点,并且影响到的点会产生连锁反应,求每个点能影响到多少个点;
题解:
一个很简单的思路:
向每个炸弹爆炸范围内的其他炸弹连一条有向边 < u , v >,表示 u 能炸到 v,最后我们从每个点开始跑 dfs,看看能到达多少个点就好了;
但是。。。
这样连边的话,最劣情况下会连 n2 条边,看一眼 n 的范围:N ≤ 500000,嗯,显然不行 ~o(* ̄▽ ̄*)o;
考虑建边优化:
不难想到一个炸弹的爆炸范围是一个长度为 2 * R [ i ] 的区间,这个区间内的所有炸弹都会被引爆,因此被引爆的炸弹也是一个连续的区间;
区间操作?你想到了什么?
线段树优化建边
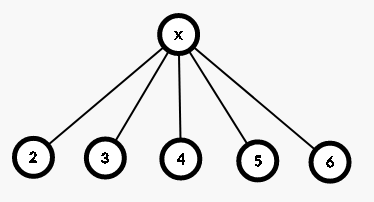
假如说一个炸弹 x 能炸到第 2~6 个炸弹,考虑怎么建边:
一般操作:
线段树优化建边:
建了 5 条边?看我的!
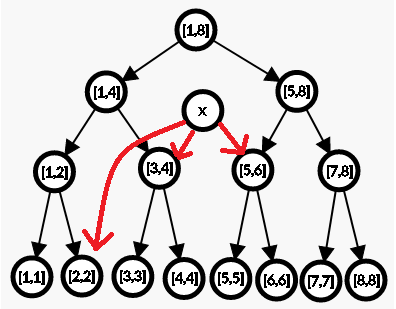
我们发现,这种建边方式只需要建 ⌈ log2 5 ⌉ = 3 条边;
看了上面的图,应该对线段树优化建边有了一个初步的认识了:
我们将线段树上原有的边也看作是我们建边的一部分,每次单点向区间建边时,向线段树区间查询那样,一直递归下去形成若干个小区间,向这些小区间建边;查询的话可以通过线段树原有的边来访问到叶子节点;
再具体一点,假如第 2 个炸弹能炸到第 4~8 个炸弹,那么建边就是这样的:
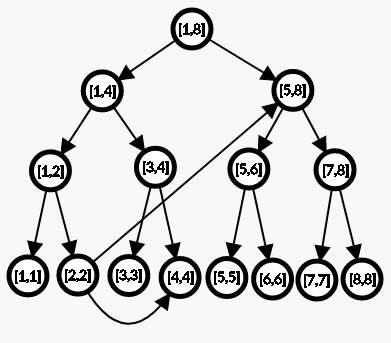
这样虽然 2 连向了 [ 5 , 8 ] 这个节点,但是我们能通过继续往下递归找到 5,6,7,8 点,从而达到优化建边的目的;
建完边了,但是这边还是有点多哦,看起来很乱,缩点试试?
缩点是可以的,假如一个环内的任意一个炸弹被引爆了,那么整个环内的所有炸弹都会被引爆,所以我们不妨将这一环内的炸弹看作是一个大炸弹;
然后我们就又用到了 tarjan 缩点;
这个就不多说了,大家应该都会;
然后对于每个强联通分量,我们都 dfs 一遍累加它能到达的所有强联通分量的大小,这个题就做完了;
woc?这么简单?
没错就是这么简单qwq!
细节提示
这道题思路挺简单的,但是里面的坑真不少,归结一下我掉进的坑,顺便提醒您们一下哦:
1. 每个强联通分量的大小不是里面的节点个数,而是里面的叶子节点个数(炸弹数),那些区间节点是不能被包含在内的;
2. dfs 的过程中,强联通分量之间可能会有重边,记得记录一下,防止重复计算;
在这里解释一下为什么有重边:
比如说这个缩点之前的奇奇怪怪的图:

嗯,是没有重边,缩完点之后呢?
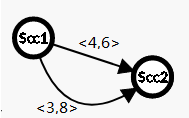
对吧。
3. 注意开 long long!
代码如下:
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<vector> using namespace std; long long read() { char ch=getchar(); long long a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<1)+(a<<3)+(ch-'0'); ch=getchar(); } return a*x; } const int N=2000000; const long long mod=1000000007; long long n,tim,top,maxn,scc_sum,edge_sum,Edge_sum; long long zb[N],R[N],num[N],where[N],head[N],Head[N],dfn[N],low[N],vis[N],st[N],scc[N]; long long ans[N],sum,size[N]; vector<int> son[N<<2]; struct node { int to,from,next; }a[N<<2],b[N<<2]; void add(int from,int to) //链表建图,应用于线段树上 { edge_sum++; a[edge_sum].next=head[from]; a[edge_sum].to=to; a[edge_sum].from=from; head[from]=edge_sum; } void build(long long node,int l,int r) { if(l==r) { where[l]=node; //坐标为l的炸弹在线段树的第node个节点 maxn=max(maxn,node); //记录线段树上最大的节点编号是多少 num[node]=1; //表示线段树上的第node个节点是叶子节点 return ; } int mid=(l+r)>>1; add(node,node<<1); add(node,node<<1|1); //向左右子树建边 build(node<<1,l,mid); //递归 build(node<<1|1,mid+1,r); } void Add(int node,int l,int r,int x,int y,int v) { if(x<=l&&r<=y) { add(v,node); //点向区间连边 return ; } int mid=(l+r)>>1; if(x<=mid) Add(node<<1,l,mid,x,y,v); if(y>mid) Add(node<<1|1,mid+1,r,x,y,v); } void tarjan(int u) //tarjan缩点 { dfn[u]=low[u]=++tim; st[++top]=u; vis[u]=1; for(int i=head[u];i;i=a[i].next) { int v=a[i].to; if(!dfn[v]) { tarjan(v); low[u]=min(low[u],low[v]); } else if(vis[v]) low[u]=min(low[u],dfn[v]); } if(low[u]==dfn[u]) { scc_sum++; while(st[top]!=u) { vis[st[top]]=0; scc[st[top]]=scc_sum; size[scc_sum]+=num[st[top]]; //坑点1:注意只记录叶子节点(炸弹)个数,而不是节点个数,num只有叶子节点才有值 top--; } //把u弹出去(表示不会do while) vis[st[top]]=0; scc[st[top]]=scc_sum; size[scc_sum]+=num[st[top]]; top--; } } void rebuild() { for(int i=1;i<=edge_sum;i++) //线段树上所有的边 { int u=a[i].from; int v=a[i].to; if(scc[u]!=scc[v]) son[scc[u]].push_back(scc[v]); //vector存图,比较方便 } } void dfs(int u) { if(ans[u]) return ; //记搜 ans[u]=size[u]; //首先一个强联通分量里的点都能互相到达 for(int i=0;i<son[u].size();i++) { int v=son[u][i]; dfs(v); //这里有个vis数组判重边用的特别精髓,给大家解释下: //vis[i]:表示本轮从哪个点到的i //想一想:假如u->v有两条边,那么在走第一条边的时候,vis[v]就会被标记u,那么在遍历第二遍的时候就直接continue了,不会重复计算 //vis数组可以不用清空 if(vis[v]==u) continue; vis[v]=u; ans[u]=(ans[u]+ans[v])%mod; } } int main() { n=read(); //n个炸弹 for(int i=1;i<=n;i++) { zb[i]=read(); //炸弹的位置,题目保证是严格递增的了 R[i]=read(); //炸弹的爆炸半径 } build(1,1,n); //线段树建树 for(int i=1;i<=n;i++) //将每个炸弹与能炸到的炸弹区间连边 { long long l=lower_bound(zb+1,zb+1+n,zb[i]-R[i])-zb; //找到能炸到的最左边的炸弹 long long r=upper_bound(zb+1,zb+1+n,zb[i]+R[i])-zb-1;//找到能炸到的最右边的炸弹 Add(1,1,n,l,r,where[i]); //连边,where[i]表示炸弹i在线段树上是哪个节点,不懂的结合上面的图体会一下 } for(int i=1;i<=maxn;i++) //缩点操作,注意这里是对线段树上的所有点进行缩点,不单单是叶子节点 { if(!dfn[i]) tarjan(i); //图不一定联通,多进行几次 } rebuild(); //对缩完点后的DAG进行重新建图 for(int i=1;i<=scc_sum;i++) dfs(i); //dfs求每个强联通分量能够到达多少个炸弹 for(int i=1;i<=n;i++) //求答案 { sum=(sum+i*ans[scc[where[i]]]%mod)%mod; //where[i]:炸弹i在线段树上是第几个节点 //scc[i]:编号为i的点在哪个强联通分量里 //ans[i]:编号为i的强联通分量能够到达多少个炸弹 //合起来就是:炸弹i在线段树上所对应的节点所在的强联通分量能到达多少个炸弹,are you ok? } printf("%lld\n",sum%mod); return 0; }
然后发现跑的有点慢能A不就行了嘛:

主要是在 dfs 的时候 vector 就显得很慢了,所以我们重建图的时候可以先用链表建图,等跑完 dfs 之后再用 vector 存儿子判重边就好了:
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<vector> using namespace std; long long read() { char ch=getchar(); long long a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<1)+(a<<3)+(ch-'0'); ch=getchar(); } return a*x; } const int N=2000000; const long long mod=1000000007; long long n,tim,top,maxn,scc_sum,edge_sum,Edge_sum; long long zb[N],R[N],num[N],where[N],head[N],Head[N],dfn[N],low[N],vis[N],st[N],scc[N]; long long ans[N],sum,size[N]; struct node { int to,from,next; }a[N<<2],b[N<<2]; void add(int from,int to) //链表建图,应用于线段树上 { edge_sum++; a[edge_sum].next=head[from]; a[edge_sum].to=to; a[edge_sum].from=from; head[from]=edge_sum; } void readd(int from,int to) { Edge_sum++; b[Edge_sum].from=from; b[Edge_sum].to=to; b[Edge_sum].next=Head[from]; Head[from]=Edge_sum; } void build(long long node,int l,int r) { if(l==r) { where[l]=node; //坐标为l的炸弹在线段树的第node个节点 maxn=max(maxn,node); //记录线段树上最大的节点编号是多少 num[node]=1; //表示线段树上的第node个节点是叶子节点 return ; } int mid=(l+r)>>1; add(node,node<<1); add(node,node<<1|1); //向左右子树建边 build(node<<1,l,mid); //递归 build(node<<1|1,mid+1,r); } void Add(int node,int l,int r,int x,int y,int v) { if(x<=l&&r<=y) { add(v,node); //点向区间连边 return ; } int mid=(l+r)>>1; if(x<=mid) Add(node<<1,l,mid,x,y,v); if(y>mid) Add(node<<1|1,mid+1,r,x,y,v); } void tarjan(int u) //tarjan缩点 { dfn[u]=low[u]=++tim; st[++top]=u; vis[u]=1; for(int i=head[u];i;i=a[i].next) { int v=a[i].to; if(!dfn[v]) { tarjan(v); low[u]=min(low[u],low[v]); } else if(vis[v]) low[u]=min(low[u],dfn[v]); } if(low[u]==dfn[u]) { scc_sum++; while(st[top]!=u) { vis[st[top]]=0; scc[st[top]]=scc_sum; size[scc_sum]+=num[st[top]]; //坑点1:注意只记录叶子节点(炸弹)个数,而不是节点个数,num只有叶子节点才有值 top--; } //把u弹出去(表示不会do while) vis[st[top]]=0; scc[st[top]]=scc_sum; size[scc_sum]+=num[st[top]]; top--; } } void rebuild() { for(int i=1;i<=edge_sum;i++) //线段树上所有的边 { int u=a[i].from; int v=a[i].to; if(scc[u]!=scc[v]) //son[scc[u]].push_back(scc[v]); //vector存图,比较方便 readd(scc[u],scc[v]); } } void dfs(int u) { /*if(ans[u]) return ; //记搜 ans[u]=size[u]; //首先一个强联通分量里的点都能互相到达 for(int i=0;i<son[u].size();i++) { int v=son[u][i]; dfs(v); //这里有个vis数组判重边用的特别精髓,给大家解释下: //vis[i]:表示本轮从哪个点到的i //想一想:假如u->v有两条边,那么在走第一条边的时候,vis[v]就会被标记u,那么在遍历第二遍的时候就直接continue了,不会重复计算 //vis数组可以不用清空 if(vis[v]==u) continue; vis[v]=u; ans[u]=(ans[u]+ans[v])%mod; }*/ if(ans[u]) return ; ans[u]=size[u]; vector<int> son; for(int i=Head[u];i;i=b[i].next) { int v=b[i].to; dfs(v);son.push_back(v); //把点u的所有儿子放进vector里 } for(int i=0;i<son.size();i++) { if(vis[son[i]]==u) continue; vis[son[i]]=u; ans[u]=(ans[u]+ans[son[i]])%mod; } } int main() { n=read(); //n个炸弹 for(int i=1;i<=n;i++) { zb[i]=read(); //炸弹的位置,题目保证是严格递增的了 R[i]=read(); //炸弹的爆炸半径 } build(1,1,n); //线段树建树 for(int i=1;i<=n;i++) //将每个炸弹与能炸到的炸弹区间连边 { long long l=lower_bound(zb+1,zb+1+n,zb[i]-R[i])-zb; //找到能炸到的最左边的炸弹 long long r=upper_bound(zb+1,zb+1+n,zb[i]+R[i])-zb-1;//找到能炸到的最右边的炸弹 Add(1,1,n,l,r,where[i]); //连边,where[i]表示炸弹i在线段树上是哪个节点,不懂的结合上面的图体会一下 } for(int i=1;i<=maxn;i++) //缩点操作,注意这里是对线段树上的所有点进行缩点,不单单是叶子节点 { if(!dfn[i]) tarjan(i); //图不一定联通,多进行几次 } rebuild(); //对缩完点后的DAG进行重新建图 for(int i=1;i<=scc_sum;i++) dfs(i); //dfs求每个强联通分量能够到达多少个炸弹 for(int i=1;i<=n;i++) //求答案 { sum=(sum+i*ans[scc[where[i]]]%mod)%mod; //where[i]:炸弹i在线段树上是第几个节点 //scc[i]:编号为i的点在哪个强联通分量里 //ans[i]:编号为i的强联通分量能够到达多少个炸弹 //合起来就是:炸弹i在线段树上所对应的节点所在的强联通分量能到达多少个炸弹,are you ok? } printf("%lld\n",sum%mod); return 0; }

嗯,果然在时间和空间上都有很大的优化哦~


