10月清北学堂培训 Day 3
今天是钟皓曦老师的讲授~
zhx:题很简单,就是恶心一些qwq~
T1



别人只删去一个字符都能AC,我双哈希+并查集只有40?我太菜了啊qwq
考虑到越短的字符串越难压缩,越长的字符串越好压缩,所以我们可以先压缩短的字符串,再压缩长的字符串,这就是全损压缩法:
全损压缩法:
1.先把所有的字符串读进来,然后按照长度从小到大排序;
2.为了压缩不成问题,我们应该从最短的字符串开始压缩;
3.依次从 a , b , c …… , x , y , z , aa , ab ……这样的顺序进行压缩,如果两个字符串相同就把它们压缩成相同的,可以发现这样的压缩方法一定是最优的;
#include<cstdio> #include<cstdlib> #include<cstring> #include<map> #include<string> #include<iostream> #include<algorithm> using namespace std; const int maxn=1010; map<string,string> ma; string z[maxn]; int n,l=1,res[233],y[maxn]; bool cmp(int a,int b) { return z[a]<z[b]; } int main() { cin >> n; for (int a=1;a<=n;a++) { cin>>z[a]; y[a]=a; } res[1]=1; sort(y+1,y+n+1,cmp); for (int a=1;a<=n;a++) { string now = z[y[a]]; if (ma.count(now)!=0) ; else { string cur = ""; for (int a=l;a>=1;a--) cur = cur + (char)(res[a]+'a'-1); ma[now] = cur; res[1]++; for (int a=1;a<=l;a++) if (res[a]>26) { res[a]=1; res[a+1]++; } if (res[l+1]) l++; } } for (int a=1;a<=n;a++) cout << ma[z[a]] << endl; return 0; }
T2


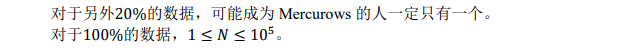
题意:
给了一棵有向树(外向树:所有边都是从根向外指的树就是外向树),并且在树上随便插了一条边,我们需要把这条边找出来,并保证这条边的编号尽可能的大 。
分两组情况:
1. 知道根节点是谁:
也就是能找到一个入度为 0 的点;
也就说明违和的边是从根下连到根下的,分为两种边:返祖边,横叉边;
但这两种边还是能归结到一种情况:有一个点的入度一定为 2;
我们就删掉连着这个入度为 2 的编号最大的边就好了;
2.不知道根节点是谁:
如果我们找不到一个入度为 0 的点的话,也就是说新加的那一条边的终点就是根节点;
那么会构成一个环,我们删掉环上编号最大的边删掉就好了;
#include<cstdio> #include<cstdlib> #include<cstring> #include<algorithm> using namespace std; const int maxn=100010; int n,en,head,tail,in[maxn],ex[maxn][2],q[maxn],f[maxn],pre[maxn][2]; bool use[maxn]; struct edge { int s,e,p; edge *next; }*v[maxn],ed[maxn]; void add_edge(int s,int e,int p) { en++; ed[en].next=v[s];v[s]=ed+en;v[s]->e=e;v[s]->p=p; in[e]++; ex[en][0]=s;ex[en][1]=e; } int get(int p) { if (f[p]==p) return p; else return get(f[p]); } void init() { en=0; memset(v,0,sizeof(v)); memset(in,0,sizeof(in)); } void read() { scanf("%d",&n); for (int a=1;a<=n;a++) { int s,e; scanf("%d%d",&s,&e); add_edge(s,e,a); } } bool work1(int p,int d) { memset(use,false,sizeof(use)); use[p]=true; head=tail=1; q[1]=p; for (;head<=tail;) { int p=q[head++]; for (edge *e=v[p];e;e=e->next) if (e->p!=d) { if (use[e->e]) return false; use[e->e]=true; pre[e->e][0]=p; pre[e->e][1]=e->p; q[++tail]=e->e; } } for (int a=1;a<=n;a++) if (!use[a]) return false; return true; } int work2(int p) { memset(use,false,sizeof(use)); use[p]=true; head=tail=1; q[1]=p; for (;head<=tail;) { int p=q[head++]; for (edge *e=v[p];e;e=e->next) { if (use[e->e]) return e->p; use[e->e]=true; q[++tail]=e->e; } } return -1; } int work() { for (int a=1;a<=n;a++) if (in[a]==2) { int p1=-1,p2=-1; for (int b=1;b<=n;b++) if (ex[b][1]==a) { if (p1==-1) p1=b; else p2=b; } if (p1>p2) swap(p1,p2); for (int b=1;b<=n;b++) if (in[b]==0) { if (work1(b,p2)) return p2; else return p1; } } for (int a=1;a<=n;a++) if (in[a]==0) return work2(a); for (int a=1;a<=n;a++) f[a]=a; for (int a=1;a<=n;a++) { int f1=get(ex[a][0]); int f2=get(ex[a][1]); if (f1==f2) { work1(ex[a][1],a); int p=ex[a][1],ans=a; while (p!=ex[a][1]) { ans=max(ans,pre[p][1]); p=pre[p][0]; } return ans; } f[f1]=f2; } return -1; } int main() { init(); read(); int p=work(); printf("%d\n",p); return 0; }
T3

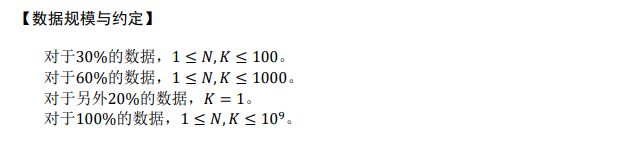
想用 dp 骗 60% 的数据来着,却成了我这三个题的最高分??
原谅我没看懂 zhx 老师的状态设置(他好像是直接设答案,不好想),我还是讲讲我的吧qwq:
状态设置:
dp [ i ][ j ]:当 Alice(下面称为 ' A ')杯内的茶剩下 i 吨, Bob(下面称为 ' B ')杯内的茶剩下 j 吨的概率是多少;
边界设置:
一开始的时候 A 和 B 都没有倒茶,所以 dp [ n ][ n ] = 1.0;
状态转移方程:
A 每次会等概率的倒出 k,2k,3k,4k 吨的茶,相应的 B 就会倒出 3k,2k,k,0 吨的茶,所以我们去枚举一下 A 倒出多少吨茶就好了:
dp [ i-x ][ j - ( 4k - x ) ] += dp [ i ][ j ] * 0.25; (i 倒出之后还剩下 i-x,j 倒出之后还剩下 j - ( 4k - x ))
for(int i=n;i>0;i--) for(int j=n;j>0;j--) for(int p=k;p<=4*k;p+=k) dp[max(i-p,0)][max(j-4*k+p,0)]+=(double)dp[i][j]*0.25; //注意如果杯里的茶不够p的话,剩下的是0而不是一个负数
答案:
这时候就要考验大家的语文水平了:
wrong answer = ( ans1 + ans2 ) / 2;
right answer = ans1 + ( ans2 / 2 );
虽然我一开始觉得是第一种,但是通过分析样例发现原来是第二种,真是坏啊qwq
先想第一种 “ A 先把茶倒光的情况 ”:
我们设最后一次 A 倒了 x 吨的茶,那么 B 倒了 4k-x 吨的茶;
既然 A 一次就倒完了,并且 B 倒了之后还有剩余,那么也就是说倒之前 A 的杯子里的茶水是不超过 x 吨的,B 的杯子里的茶水是超过了 4k-x 吨的;
那么我们把这些所有情况加起来就好了:
for(int p=k;p<=4*k;p+=k) //A先把茶倒完的情况:枚举A最后一次倒了多少多少 for(int i=1;i<=p;i++) for(int j=n;j>4*k-p;j--) //枚举B最后一次倒之前倒了多少 ans1+=dp[i][j]*0.25;
然后想第二种 “ A 和 B 同时把茶倒光的情况 ”:
也就是说,最后一次倒茶时,A 的杯子内的茶水是不超过 x 吨的,同时 B 的杯子内的茶水是不超过 4k-x 吨的:
for(int p=k;p<=4*k;p+=k) //同时倒完的情况:枚举A最后一次倒了多少 for(int i=1;i<=p;i++) for(int j=1;j<=4*k-p;j++) ans2+=dp[i][j]*0.25;
然后输出 ans1 + ans2 / 2 就好了;
但是。。。这个题 n,k <= 1e9,你的算法是 O ( n2 ) 的 ε=(´ο`*))) 唉;
貌似 k 没用?
考虑到其实 n=10,k=2 和 n=5,k=1 是一种情况,它们的最后答案是一样的;
假如 n = 10, k = 5 和 n = 2 , k = 1 是一样的!
那么我们就可以做一个转化:
n => n / k (上取整),k => 1;
那么现在的问题就变成:给你一个 n,问概率。
打表大法好啊!而且这个题就可以打表做qwq 。
两种方法打表:
1. 爆搜,而且可以加上记忆化;
状态设置:f [ i ][ j ] :
f [ 0 ][ i ] = 1.0;
f [ i ][ 0 ] = 0.0;
f [ 0 ][ 0 ] = 0.5;
考虑怎么转移:
f [ i ][ j ] = 0.25 * ( f [ i-4 ][ j ] + f [ i-3 ][ j-1 ] + f [ i-2 ][ j-2 ] + f [ i-1 ][ j-3 ] );
然后我们可以发现,当 n 超过了 235 的时候(n/k 后的新 n),答案就是 1 了 。
所以我们再加一个特判,就满分喽~
我的 lj 代码:
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> #include<queue> using namespace std; int read() { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<1)+(a<<3)+(ch-'0'); ch=getchar(); } return a*x; } int n,k; double dp[4001][4001]; double ans1,ans2; int main() { //freopen("tea.in","r",stdin); //freopen("tea.out","w",stdout); n=read();k=read(); if(n%k!=0) n=n/k+1; else n=n/k; k=1; if(n>300) { printf("1.000000"); return 0; } dp[n][n]=1.0; for(int i=n;i>0;i--) for(int j=n;j>0;j--) for(int p=k;p<=4*k;p+=k) { //printf("dp[%d][%d]:%lf\n",i,j,dp[i][j]); dp[max(i-p,0)][max(j-4*k+p,0)]+=(double)dp[i][j]*0.25; //printf("dp[%d][%d]:%lf\n",max(i-p,0),max(j-4*k+p,0),dp[max(i-p,0)][max(j-4*k+p,0)]); } for(int p=k;p<=4*k;p+=k) //A先把茶倒完的情况:枚举A最后一次倒了多少多少 for(int i=1;i<=p;i++) for(int j=n;j>4*k-p;j--) //枚举B最后一次倒之前倒了多少 ans1+=dp[i][j]*0.25; for(int p=k;p<=4*k;p+=k) //同时倒完的情况:枚举A最后一次倒了多少 for(int i=1;i<=p;i++) for(int j=1;j<=4*k-p;j++) ans2+=dp[i][j]*0.25; //printf("%lf %lf\n",ans1,ans2); printf("%.6lf",ans1+ans2*0.5); return 0; }
标程超短代码:
#include<cstdio> #include<cstdlib> #include<cstring> using namespace std; const int maxn=201; int n,k; double f[maxn][maxn]; bool g[maxn][maxn]; double dfs(int n,int m) { if (n<=0 && m<=0) return 0.5; if (n<=0) return 1.0; if (m<=0) return 0.0; if (g[n][m]) return f[n][m]; g[n][m]=true; for (int a=1;a<=4;a++) f[n][m]+=0.25*dfs(n-a,m-4+a); return f[n][m]; } double work(int n,int k) { if (n/k>=maxn) return 1.0; return dfs((n/k)+(n%k?1:0),(n/k)+(n%k?1:0)); } int main() { scanf("%d%d",&n,&k); printf("%.6lf\n",work(n,k)); return 0; }
图论题选讲

Problem -1 是什么操作?
先假设没有障碍的情况:
因为在同一行或同一列的两个物体能互相看见,也就是说一个物体会用掉一行和一列;
如果我们从第 i 行连向了第 j 列,那么就说明 (i,j)这个位置可以放上物体;
我们放上一个障碍物,就可以看做把那一行和列分成了两个部分;
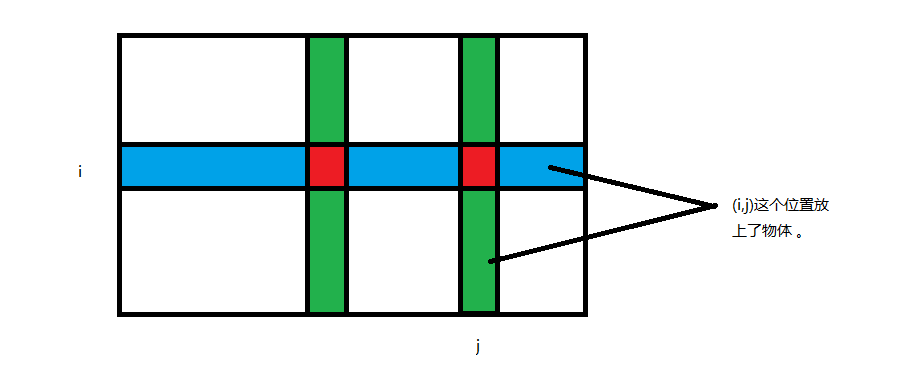
最后答案:我们最多能匹配多少对,就是我们最多能放多少个物体;
一遍匈牙利算法或网络流 Dinic 算法跑最大匹配就好了;

考虑到一开始的两个 1 既不能在同一行,也不能在同一列;
所以我们只需要判断是否有 n 个 1 都不在同一行或同一列上;
这就类似于上一个题啊qwq;
第 i 行连向第 j 列表示(i,j)这个位置的 1 可以选;
最后我们只需要看看最大匹配数是否是 n 就好了;
如果我们找不到的话,就说明无解!
2-SAT 问题:
有 n 个变量,每一个变量都是 bool 类型的,除了这 n 个变量以外,我们还有 m 个关系表达式,关系表达式差不多是这样的:
x1 & x2 = false(注意每个表达式只会有两个变量)
问给出 m 个关系表达式后,能否给这 n 个变量找出一个赋值的方法,使得满足所有的表达式;
核心问题只需要考虑有没有解;
对于每个变量都只有两种取值:0 / 1,那么对于每个点,我们把每个变量看成 0点和 1点;
假如我们有一个关系:x1 & x2 = false;
说明 x1 和 x2 中一定有一个为 false;
那么我们可以从 x1 的 true 连向 x2 的 false,从 x2 的 true 连向 x1 的 false;
要注意只有关系明确的时候才能建边;
解释一下:
如果 x1 的值为 true ,那么如果我们 x2 的值再为 true 的话,就不满足 “ x1 & x2 = false ” 这个式子了,所以如果 x1 为 true 的话是能明确推出 x2 为 false 的;
我们可以从 x2 的 flase 向 x1 的 true 连边吗?这样也能满足关系式;
显然不能,因为你如果 x2 为 false 的话,x1 为 true 或 false 是都可以的,这不是明确的关系,我们不能建边;
所以一般的建边方式为:
若 xa = p 或 xb = q 中至少有一个满足,那么我们建两条边:
xa (¬p) -> xb (q)
xb (¬q) -> xa (p)
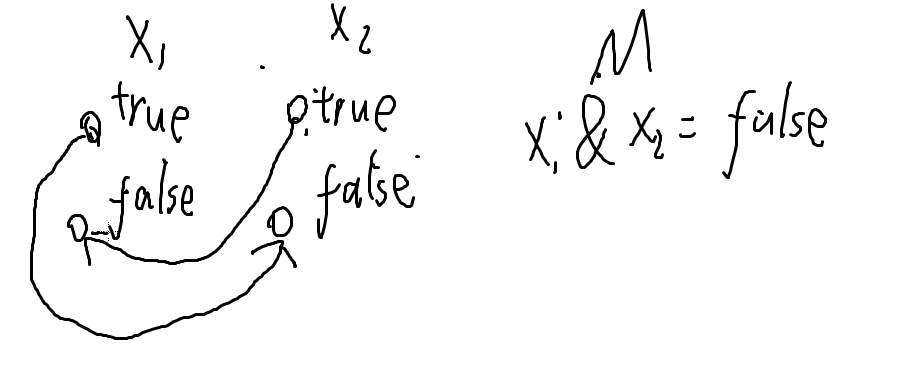
如果一个变量必须等于 true,那么我们从这个点的 false 连向这个点的 true;
表示我们从 false 走也会走到 true,也就是说只能等于 true;

怎么判断是否有解?
假如说我们从一个点的 true 走到了它自己的 false,那么就说明这个点只能是 false;假如我们从一个点的 false 走到了它自己的 true,那么久说明这个点只能是 true;以上两种情况是有解的 。
无解的情况就是:某一个变量的 false 能走到 true,从 true 也能走到 false,也就是说,某一个变量的两个取值在同一个强连通分量内的话,就说明无解。
所有的 2-SAT 问题都是这么做;

最大化最小值问题,二分喽~
二分爆炸半径的最小值 r,看 r 是否合法;
既然最小值是 r 了,我们不妨直接让所有的炸弹的爆炸范围都是 r;
我们看到每一组都有两种取值,自然对应得就是 2-SAT 了;
建图:

假如我们第一组的第一个炸弹能扎到第二组的第一个炸弹,那么就说明这两个炸弹不能同时选,所以我们从第一组的第一个炸弹向第二组的第二个炸弹连一条边;反之,我们从第一组的第二个炸弹向第二组的第一个炸弹连边;(注意连有向边)
每次 n2 暴力建边,然后 tarjan 判断是否合法就好了;
合法就向更大的 r 去枚举,直至不合法 ,此时的 r 就是答案了。

给你一个 n * m 的棋盘,上面有些格子是黑色的,有些格子是白色的,还有一些障碍(不能放骨牌),现在你有一种类似于 ' L ' 型的骨牌,两端是白色的,中间是黑色的,要求将骨牌放在棋盘上,使得黑色部分放在黑色格子上,白色部分放在白色格子上,每个格子只能被覆盖一次(只能放一个骨牌),问能否能将整个棋盘覆盖满?
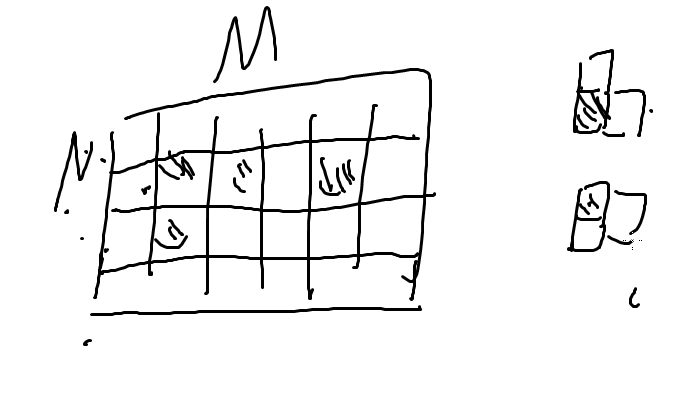
我们考虑将黑点拆点,使得一个黑格子对于一个白格子;
但是有一个问题:我们可能搞出来的不是 ' L ' 型;
所以我们将白格子分为上下白格子和左右白格子;
这样的话,一个黑格子对应一个上下白格子,一个黑格子对应一个左右白格子,合起来的话就能保证它是一个 ' L ' 型的了;
对于更大的数据,只能用 2-SAT 做了:
看到这道题只是判断有没有解,那么自然就想到了 2-SAT 。
我们可以为每个黑点造两个变量:左右变量和上下变量,每个变量有两种取值,这样就变成了 2-sat 问题 。
点建好了,边怎么建?
如果两个黑格子的曼哈顿距离不超过 2,它们之间就有可能会冲突:
假设我们有两个黑格子的分布是:左上和右下,那么它们的建边关系就是:
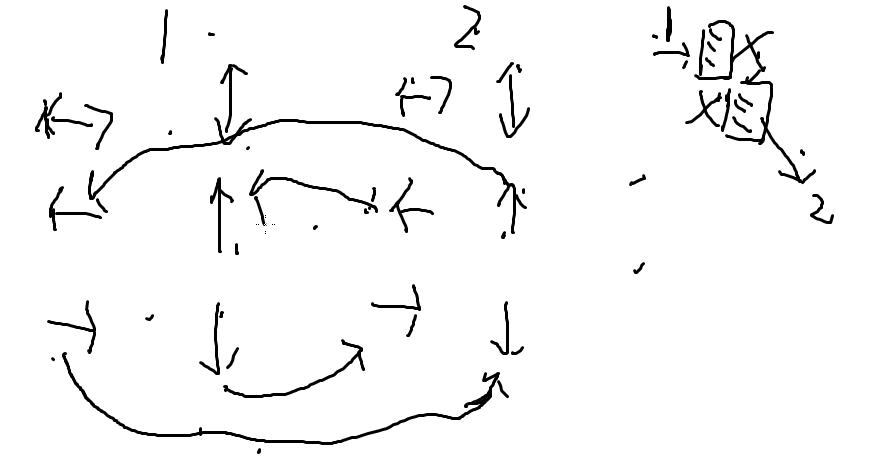
实际也就 6 种情况,我们分别根据它们的位置关系建边就可以了:
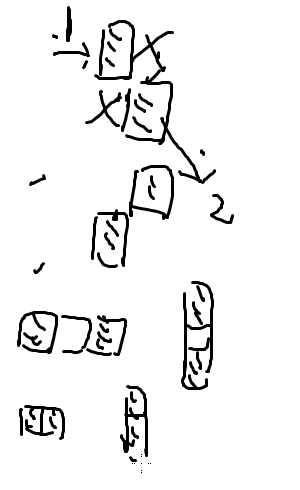
然后我们跑一遍 tarjan 判断其是否有解;
总时间复杂度 O ( nm );

我们依然可以用 2-SAT 做;
我们考虑每个提案到底是通过还是否决;
我们先考虑每个人投一票的情况:
假如一个人对了一号提案投了反对票,由于要有一半以上的提案和投票情况相符,所以这个提案一定否决,我们从一号提案的通过连向否决,表示一号提案一定被否决:
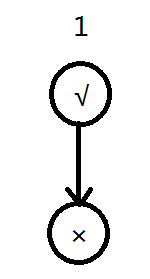
发现投两票和投一票的情况一样,也是需要所投的两个提案必须都和投票情况相符;
考虑投三票的情况:假设一个人投了三、四、五号提案的通过,假如三号提案被否决了,由于至少要有一半以上的提案符合投票情况,所以剩下的四、五号提案是一定被通过的,所以我们可以从三号提案的否决分别连向四、五号提案的通过;同理我们再从四号提案的否决连向三、五号提案的通过,从五号提案的否决连向三、四号提案的通过:
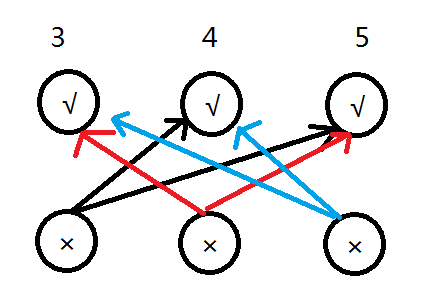
发现投四票的情况也是和投三票的情况一样,一个不满足剩下的三个都必须满足;
答案:
如果一个提案能从通过走到否决,那么说明这个提案一定会被否决;如果一个提案能从否决走到通过,那么说明这个提案一定会被通过;如果既能从通过走到否决,也能从否决走到通过,那么说明这个提案不一定被通过或者否决;

由于树是个二分图,所以我们可以从树的角度去考虑; 把一张图变成一棵树有两种方法:
1.生成树;
2.缩点;
一张图如果不是二分图,就说明有基环存在,所以我们要把所有的基环都干掉,所以我们所需要干掉的这条边就是所有基环的交集的那条边;
那么怎么求所有基环的交集?
我们先在这个图上随便求一棵生成树,然后我们求完生成树后,所有的边分成了两类:树边和非树边;
如果没有不在树上的边,就说明这个图是二分图了;如果有一条不在树上的边,连了两个颜色一样的点,形成了一个基环,我们需要破坏掉基环;
如果我们只能找到一条非树边,那就说明这一张图里面就一个基环,那么我们删掉这个基环上的任意一条边都可以使这个图变成二分图;
如果说存在两条及以上的基环,我们并不能通过删除一条非树边来搞掉所有基环,此时我们要删的就是一条树边;
如果一条非树边形成了一个基环,我们就将这个基环上的所有边的权值+1;这么瞎搞一通以后,如果我们发现有一条树边的权值等于基环的个数,也就是说这条树边被所有的基环包含在内,所以这一条边就是答案了;
至于+1的操作,我们可以使用树上差分或者树链剖分来实现;

看着 A 国人少条件少,先欺负分析 A 国:
化简一下 A 国交朋友的条件:
x1 ^ x2 %2 = 1;
保证两个友善值异或后是奇数,也就是说两个数表示成二进制后最右边的那一位不同,也就是说两个人的友善值一奇一偶;
那么最后的朋友圈中 A 国就只有 2 个人(超过了2人的话肯定有两个人的奇偶性相同,那么就不会是朋友了);
所以现在的问题就是找 B 国最大的朋友圈;
给你一张图让你求最大团是 NPC 问题,那么这个图不是随便给你的,一定是含有某个神奇的性质的;
我们来分析 B 国交朋友的条件:
第一个条件:x1 ^ x2 % 2 = 0;
与 A 国的分析情况相似,也就是说友善值同奇偶的人可以互相交朋友;
第二个条件:x1 | x2 在二进制表示上有奇数个1;
这个条件看起来有点奇怪,但可以确定的是这个条件使得在 B 国一奇一偶的人也可以交朋友,那么总体来说 B 国的情况就是这个亚子:
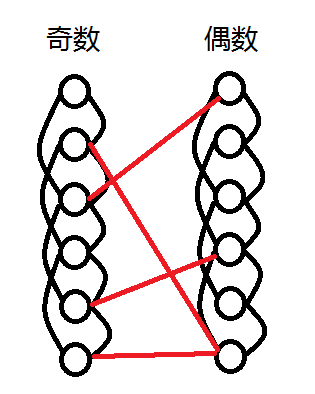
看这个亚子有点像二分图呐,但是我们知道二分图两侧的点之间是没有连边的呀,但是这个图却两两连了边(没画全,其实是不想画了,意思意思就好),然后我们发现这个图的补图是一个二分图!
二分图的补图:
反图的最大独立集就是原图的最大团;
我们要在补图中找到一个最大的独立集,使得原图求出来的是最大团;
每有一个匹配,我们所能够选的点就少一个,所以最后的答案就是:n+m - 最大匹配;

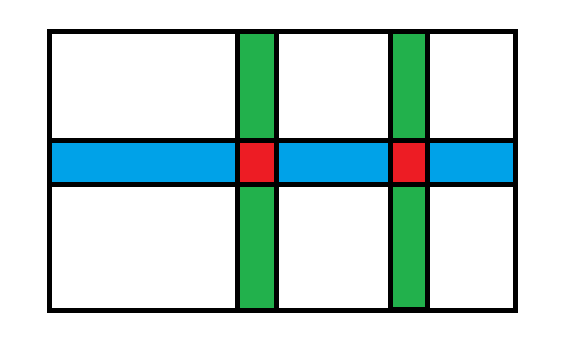
每种颜色的格子最多两个?神奇的数字 2!
假设我们考虑每种颜色的格子只有 1 个的话,那么每种颜色的格子要去的方向是固定的;
那么我们肯定能通过 “ 行操作 + 列操作 + 行操作 ” 或 “ 列操作 + 行操作 + 列操作 ” 来完成;
那么最后的答案一定不超过:min(ca+2cb ,cb + 2ca);
如果只有一个系列的操作,我们直接通过暴力去求;
如果需要通过两个系列去解决呢?
如果我们发现同一行的两个格子要到同一列去,或者同一列的两个格子要去同一行去,那么我们就不能省去第三步;
但是原题每种颜色都至少有 2 个呀?
我们可以 dfs 每个格子去哪里,但是这样的话时间复杂度为 O ( 245000 );
假设一种颜色的两个初始位置 a,b ,在目标状态移动到了 A,B;
那么只有两种取值:
1. a -> A,b -> B;
2. a -> B,b -> A;
如果 a 和 c 在同一行,A 和 C 在同一列,那么就说明我们不能通过两部操作来完成;
如果 a 去 A , b 去 B,那么 c 只能去 D,同样 d 去 c;
如果 a 去 B , b 去 A,那么 c 只能去 C,同样 d 去 D;