8月清北学堂培训 Day4

今天上午是赵和旭老师的讲授~

概率与期望 dp

概率 

某个事件 A 发生的可能性的大小，称之为事件 A 的概率，记作 P ( A ) 。

假设某事的所有可能结果有 n 种，每种结果都是等概率，事件 A 涵盖其中的 m 种，那么 P ( A ) = m/n。

例如投掷一枚骰子，点数小于 3 的概率为 2/6=1/3 。

如果两个事件 A 和 B 所涵盖的结果没有交集，那么 P ( A或B发生 )= P ( A ) + P ( B ) ；

还是掷骰子： P (点数小于3或点数大于4) = 2/6 + 2/6 = 2/3 ；

如果A和B所涵盖的结果有交集，那么 P (A或B发生) = P ( A ) + P ( B ) - P (A与B同时发生) ；

P (点数小于3或点数为偶数) = 2/6 + 3/6 - 1/6 = 2/3；

记事件 B 为 “ 事件 A 不发生 ”

那么 P ( A ) + P ( B ) = 1，即 P ( B ) = 1- P ( A ) ；

P(点数不小于3) = 1 - 2/6 = 2/3 ；

在两个互不干扰的事中，事件 A 在其中一件事中，事件 B 在另外一件事中，那么 P(A与B同时发生) = P(A) * P(B)

掷两个骰子，P(第一个点数小于3且第二个点数为偶数) = (2/6) * (3/6) = 1/6；

 

期望

事件 A 有多种结果，记其结果的大小为 x，那么 x 的期望值表示事件 A 的结果的平均大小，记作 E ( x ) 。 

E ( x ) = 每种结果的大小与其概率的乘积的和。

例如，记掷一枚骰子的点数为 x 

E ( x ) = 1 * (1/6) + 2 * (1/6) + 3 * (1/6) + 4 * (1/6) + 5 * (1/6) + 6 * (1/6) = 7/2 ；

若 c 为常数，那么：  E (x+c) = E(x) + c，E (c*x) = c * E (x)；

记两个事件的结果分别为 x , y 

 E(x+y) = E(x) + E(y)；期望的线性性质

例如：E (语文成绩+数学成绩) = E(语文成绩) + E(数学成绩)；

若两个事件互相独立，E(x*y) = E(x) * E(y) ；

E(语文成绩*数学成绩) = E(语文成绩) * E(数学成绩)；

 

概率和期望的计算

概率与期望的计算有一个共同的计算技巧：

若事件所产生的所有方案都是等概率的，那么一些概率与期望即可转化为一个计数问题，算出后再除以总方案数即可。

如求事件符合条件 A 的概率，则转化为对符合 A 的方案数的计数问题；若求方案的某种价值的期望值，则转化为所有方案的价值总和的计数问题。

概率与期望的计算也经常用的其加法和乘法规则。

尤其是期望的加法规则，在期望的计算中十分常用。如求最大值与最小值之差的期望，则分别求二者的期望值再作差即可。

应用乘法规则时，要注意事件是否互相独立。

概率与期望还可以通过列方程的方法计算：

有 4 张卡片，写着 0,1,2,3，每次抽出一张并放回，反复抽，抽出 0 为止。问抽取的次数的期望值。

设抽取次数为 x，则： 
x = 1 + x * 3/4 

x = 4

大家一定一脸懵逼吧（大佬除外哦），我粗略地解释下：

我们分成两种情况：

1. 抽到了 0 ，那造成的结果是什么呢？我们不用再抽了！

那么这种情况的期望就是：1/4 * 0（还需要抽 0 次，也就是说不用抽了）；

2. 没抽到 0，那造成的影响就是还要继续抽！由于我们每次抽的卡片都要放回，也就是说如果没有抽到 0 的话每次重新抽的局面都是一样的，那么不就是我们一开始的样子嘛？那还需要抽几次？？？当然就是我们一开始设的 x 啦！

那么这种情况的期望就是：3/4 * x；

但由于我们一开始抽了一次（但不知道抽没抽中），所以答案要加一；

答案就是 x = 1/4 * 0 + 3/4 * x + 1 = 1 + x * 3/4；

比较常见一种计算方法就是概率 dp 与期望 dp 。

 

概率DP期望DP

 

比较简单的概率 dp

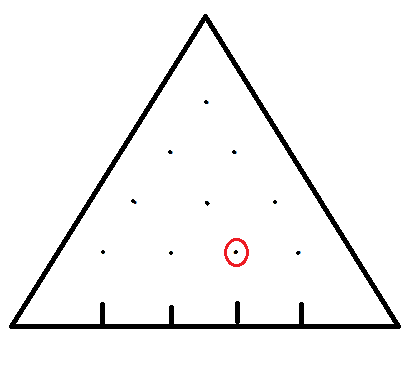
设 f [ i ][ j ] 为小球经过第 i 行第 j 列的概率。

f [1 ][ 1 ] = 1 （即起状态概率为 1）

 

我们考虑有几种状态能走到红点：

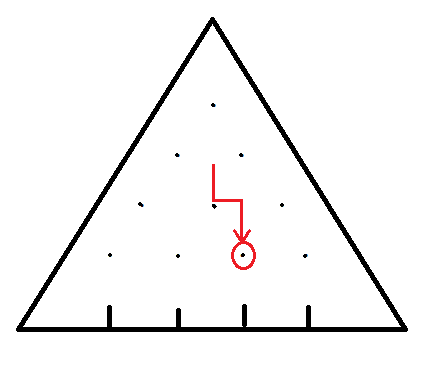
左上方如果有钉子的话能走到：

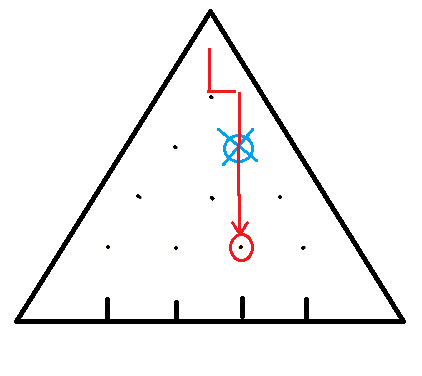
右上方如果有钉子的话能走到：

上两层如果没有钉子的话能走到：

 

 那么我们就得出了状态转移方程：

f [ i ][ j ] = f [ i-1 ][ j-1 ] * [ ( i-1 , j-1 ) 有钉子 ] * 1/2 + f [ i-1 ][ j ] * [ ( i-1 , j ) 有钉子 ] * 1/2  + f [ i-2 ][ j-1 ] * [ ( i-2 , j-1 ) 没有钉子 ]

至于分数输出，自定义分数数据类型并用 gcd 化简分数即可。 

 

题目约定了每个点的入度和出度均为1，因此最终的图一定是若干个环（要不然的话定会有至少一个箱子根本无法打开）。

每个环都至少选择一个点即可满足要求。求概率，实际上就是求方案数， 最后再除以总方案数即可。

预处理出每个环的点数 c [ i ] 以及其后缀和 sum [ i ] 。

设 f [ i ][ j ] 表示前 i 个环中选出 j 个点，满足最终条件每个环都选的方案数。 初始化 f [ 0 ][ 0 ] = 1 。

枚举 i 和 前 i 个环选的点数 j 、第 i 个环选的点数 k。

可得：

 

 

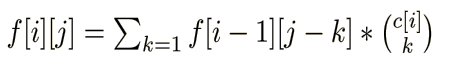
首先容易得到一个简单的做法。

设 f ( i , j ) 为走 i 步之后到达 j 的概率，那么我们去枚举所有能直接到 j 的结点 u，那么从 u 点到达 j 的概率就是先到达 u 的概率 * （1/ d_u），再求和： 

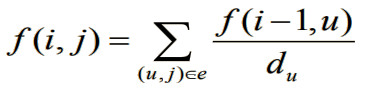
题目给出了走第一步的概率了，到达每个点的概率都是：d_j / 2m，即：

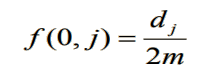
我们接着走，这次走的话只能顺着邻边了，考虑到当前苹果树 j 有 d_j 条出边，那么选择每一条出边的概率就是 1 / d_j ，那么我们到达每个点的概率就是：d_j / 2m * ( 1 / d_j ) = 1 / 2m；

那么我们现在考虑每个点被第二步走到的概率，对于一个点 j，如果它是在第二步中被走到，那么一定是从它邻边上的点转移过来的，我们在上面已经求出了走第二步的概率是 1 / 2m，考虑到第 j 个点有 d_j 个直接连通的点，我们将这些点的概率相加就是第二步走到点 j 的概率，即：

那么同理我们可以得到：

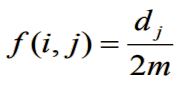
如何求答案呢？

我们两层循环，外层枚举走了几步（1~k），内层枚举最后一步走到了哪里（1~n），求期望（得分 * 概率）：

那么这个题就做完了。

 

 

 

设 f [ i ][ a ][ b ][ c ] 表示还要进行 i 轮攻击，三种血量的奴隶主数量分别为 a（一滴血）b（两滴血）c（三滴血） 时， 接下来英雄受到的期望总伤害。

转移只要枚举当前攻击到的是英雄还是哪种奴隶主即可。

初始 f [ 0 ][ a ][ b ][ c ] = 0。（a，b，c 枚举只要和小于等于 7 就行）；

考虑状态转移方程：

我们记场上现在有 sum = 1 + a + b + c 个人；

有四种情况转移过来：

1. 如果我们不幸打到了英雄，算一下打到英雄的概率是：1 / sum  ；

那么它从上个局面转移过来的期望就是：f [ i-1 ][ a ][ b ][ c ] += f [ i ][ a ][ b ][ c ] / sum；（上个局面的期望 * 转移概率）

还得掉血是吧？期望掉血 = 掉血 * 掉血概率，即 f [ i-1 ][ a ][ b ][ c ] += 1 * 1 / sum；

综上，f [ i-1 ][ a ][ b ][ c ] += f [ i ][ a ][ b ][ c ] / sum + 1 * 1 / sum ；

即 f [ i-1 ][ a ][ b ][ c ] += （f [ i ][ a ][ b ][ c ] + 1）/ sum；

 

2. 如果我们打到了只有一滴血的奴隶主，算一下打到的概率是：a / sum ；

由于它只有一滴血，打了一下之后就死了鸭？（好惨），但是又不会召唤新的奴隶主；

那么它从上个局面转移过来的期望就是：f [ i-1 ][ a ][ b ][ c ] += f [ i ][ a+1 ][ b ][ c ] / sum；（上个局面的期望 * 转移概率）

 

3. 如果我们打到了有两滴血的奴隶主，算一下打到的概率是：b / sum ；

打了两滴血的奴隶主后，如果场上的奴隶主少于 7 个的话，它是会召唤一个三滴血的奴隶主的，所以我们要分情况讨论：

（1）如果场上的人数为 7，那么就说明无需召唤：

f [ i-1 ][ a ][ b ][ c ] += f [ i ][ a-1 ][ b+1 ][ c ] / sum；（两滴血的少了一个，一滴血的多了一个）

（2）如果场上的人数小于 7，那么说明打一下后会召唤一个血为 3 的奴隶主：

f [ i-1 ][ a ][ b ][ c ] += f [ i ][ a-1 ][ b+1 ][ c-1 ] / sum；（召唤一个三滴血的奴隶主，所以 c + 1）

 

4. 如果我们打到了有三滴血的奴隶主，算一下打到的概率是：c / sum ；

打了三滴血的奴隶主后，如果场上的奴隶主少于 7 个的话，它也是会召唤一个三滴血的奴隶主的，所以我们要分情况讨论：

（1）如果场上的人数为 7，那么就说明无需召唤：

f [ i-1 ][ a ][ b ][ c ] += f [ i ][ a ][ b-1 ][ c+1 ] / sum；（三滴血的少了一个，两滴血的多了一个）

（2）如果场上的人数小于 7，那么说明打一下后会召唤一个血为 3 的奴隶主：

f [ i-1 ][ a ][ b ][ c ] += f [ i ][ a ][ b-1 ][ c+1-1 ] / sum；（打了一下三滴血的奴隶主，要减一，但又召唤一个，所以不变）；

 

每次询问可以 O ( 1 ) 回答。 

 

首先可以 floyd 求出任意两点间最短路径。

可以想到一个显然的 dp 状态：f [ i ][ j ][ 0/1 ] 表示前 i 个课程申请了 j 次，且第 i 个是否申请时的最小期望值。

转移示例：

f [ i ][ j ][ 0 ] = Max { f [ i-1 ][ j ][ 0 ] + dis ( a [ i-1 ] , a [ i ] ) ， f [ i-1 ][ j ][ 1 ] + k [ i-1 ] * dis ( b [ i-1 ] , a [ i ] ) + ( 1- k [ i-1 ] ) * dis ( a [ i-1 ] , a [ i ] ) }

f [ i ][ j ][ 1 ] 也是同理，只需要考虑 i 和 i-1 都是否申请上即可。

时间复杂度 O ( v³ + nm ) 。 

 

当你要做是否吃某个宝物的决策时，如果你知道以吃或不吃的状态进入接下来的几轮游戏时分别的期望得分是多少，那么就可以择优进行决策。

 

于是设 f [ i ][ S ] 为进行到第 i 轮游戏，吃过的宝物集合为 S 时，接下来能得到的最大期望得分。

但是我们发现顺推的话会有不合法的情况，所以我们选择逆推！

 

f [ i ][ S ] = ( ∑ Max { f [ i+1 ][ S ] , f [ i+1 ][ S | （1 << k-1） ] + a [ k ]   } ) / m ；

初始 f [ 0 ][ S ] = 0，ans = f [ 1 ][ 0 ] 。

 

最套路的斜率优化

斜率优化本身是个很套路的东西。

它有一个很标准的形式，以及很套路的解法。

 

dp 设计很简单，主要是优化。

我们设 dp [ i ] 表示输出到 i 的时候最少的花费，S [ i ] 表示从 a [ 1 ] 到 a [ i-1 ] 的数字和。注意这里为了方便起见前缀和与一般的有区别，就是让式子看起来更好看，没别的特殊意义。
dp [ i ] = min { dp [ j ] + ( S [ i+1 ] - S [ j ] )² + M } ( j < i ) ；
然后就是 O ( N² ) 复杂度。

那么我们想，能否在 O ( 1 ) 时间内找到所有转移里最优的那个呢？

我们假设在求解 dp [ i ] 时，存在 j , k ( j > k ) 使得从 j 转移比从 k 转移更优，那么需要满足条件：
dp [ j ] + ( S [ i+1 ] - S [ j ] )² + M < dp [ k ] + ( S [ i+1 ] - S [ k ] )² + M（这里大于号小于号具体根据题目要求，这里求得是最小花费）
展开上式：
dp [ j ] + S [ i+1 ]² + S [ j ]² - 2 * S [ i+1 ] * S [ j ] + M < dp [ k ] + S [ i+1 ]² + S [ k ]² - 2 * S [ i+1 ] * S [ k ] + M ；

消去再合并同类项得：

dp [ j ] + S [ j ]² - 2 * S [ i+1 ] * S [ j ]  < dp [ k ] + S [ k ]² - 2 * S [ i+1 ] * S [ k ] ； 

将与 i 有关的项移到右边，其余的移到左边：

dp [ j ] + S [ j ]²  - ( dp [ k ] + S [ k ]² ) < 2 * S [ i+1 ] * S [ j ] - 2 * S [ i+1 ] * S [ k ]；

合并同类项：

dp [ j ] + S [ j ]²  - ( dp [ k ] + S [ k ]² ) < 2 * S [ i+1 ] * ( S [ j ] - S [ k ] )；

再把不关于 i 的移到左边去：

[ ( dp [ j ] + S [ j ]² ) - ( dp [ k ] + S [ k ]² )  ] / ( S [ j ] - S [ k ] ) < 2 * S [ i+1 ] ；

 

到这里我们的式子就化简完了，我们对它进行一波分析：

看到我们设的是：j > k，且 j 优于 k ，那么就会出现上面的式子；

也就是说，如果我们出现了上面的式子，那么就说明 j 比 k 优，也就是说靠后者（数值大）更优；

反之若出现：[ ( dp [ j ] + S [ j ]² ) - ( dp [ k ] + S [ k ]² )  ] / ( S [ j ] - S [ k ] ) >  2 * S [ i+1 ]  的话，那么说明靠前者（数值小）更优；

那么我们继续推式子：

设 f [ x ] = dp [ x ] + S [ x ]² ；

那么原式就成了：( f [ j ] - f [ k ] ) / ( S [ j ] - S [ k ] ) < 2 * S [ i+1 ]；

那把 ( S [ i ] , f [ i ] ) 看作一个点，左边就是斜率的形式了。

当一个数的 dp 值求完了，它的 f 值也跟着确定，我们就可以在空间中绘制出点 ( s [ i ] , f [ i ] ) 。这个点代表已经求出 dp 值的一个点。

当我们要求解 dp [ t ] 时，如果可用的集合里存在这样三个点，位置关系如图所示：

可以锁定 jk 的斜率是大于 ij 的斜率的；

这时候他们和 2 * S [ t+1 ] 的关系有3种： 

此时 k 优于 j，j 优于 i ，最优的是 k；

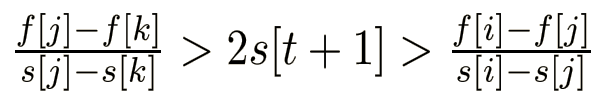
此时 k 优于 j，i 优于 j，最优的是 i，k；

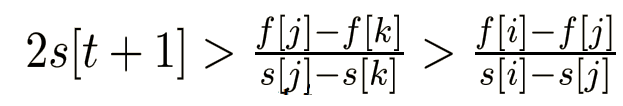
此时 j 优于 k，i 优于 j，最优的是 i；

我们看到，无论是哪种情况，最优的都不是 j，而 j 恰好是最中间的位置；

那么也就是说，如果有三个点之间的斜率长上图中的这个亚子，那么中间的点一定不是最优的，我们可以舍去；

 

综上，不管什么样的 S [ t+1 ]，从 j 转移都不会是最佳方案。

那么用一个数据结构维护一个凸包（下凸），每加入一个点就删去一些点，使其维持凸包的形态。最优转移一定在这个凸包中。

下凸的凸包边斜率增加，上凸的凸包边斜率减小。

在凸包里，谁又是最最优呢？

首先一定数据结构里的凸包一定会是这样的：

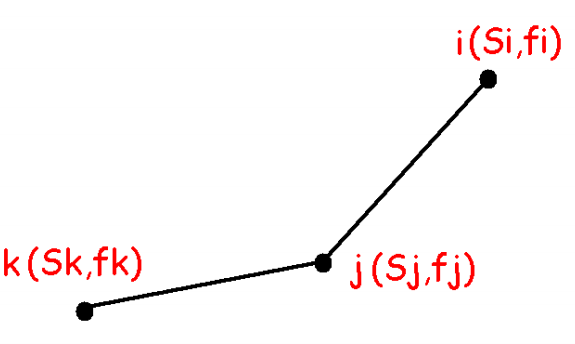
我们可以锁定 ij 的斜率大于 jk 的斜率；

那么我们还是分三种情况来讨论：

此时 j 优于 i，k 优于 j，最优的是 k；

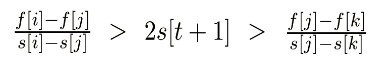
此时 j 优于 i，j 优于 k，最优的是 j；

此时 i 优于 j，j 优于 k，最优的是 i；

我们发现，在下凸包的情况中，哪种情况的最优解都不一样，也就是说，每个点都有可能成为答案，所以我们不能删点，要具体看 2 * S [ t+1 ] 的值； 

我们现在有一个图，如何去找决策点？

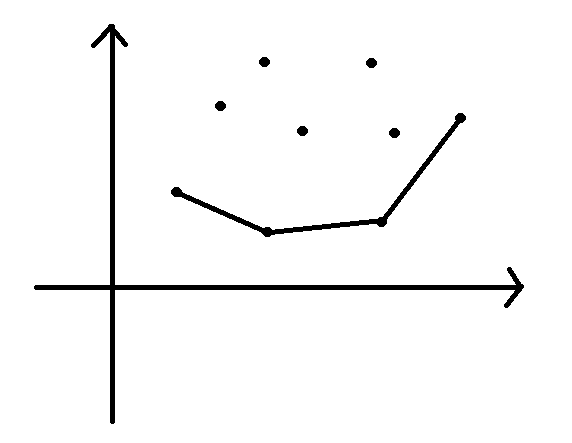
很显然，决策点就是下面的那些点，为什么上面的点不要选嘞？

假如我们选了上面的某些点：

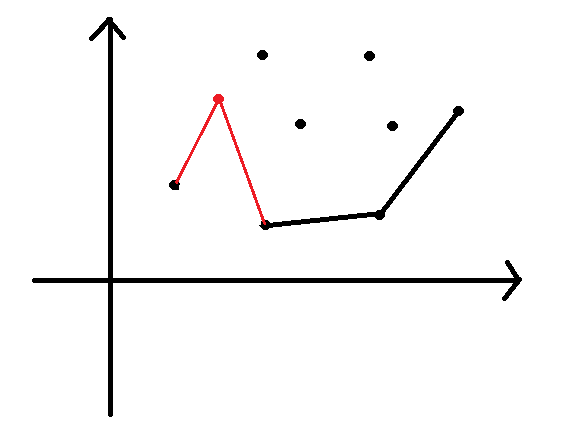
那么一定会形成斜率递减的下凸包（红色边），根据我们上面的结论，完全可以删掉上凸包的顶点，即我们可以删掉上面的点而将下面的两点连起来，也就是我们只选择下面的两个点；由此推向全图可知决策点要选最下面的点；

假设 ij 的斜率 >2 * S [ t+1 ] 且 kj 的斜率 < 2 * S [ t+1 ] 从图形特点我们可以发现 j 点比所有比 k 小的点都优，比所有比 i 大的也优。

所以对于我们二分查找斜率比 2 * S [ t+1 ] 小的编号最大的点，就是最优的转移点 。由于 S [ i ] 也满足单调性，那么如果一个点不是 i 的最优点了，那么肯定也不是 i+1 的，我们还可以直接维护一个单调队列就能解决这个问题。

单调队列每次从后加时，维护凸包 。

每次新计算一个 i 的 dp 值，从单调队列队首弹出那些不可能再合法的元素 。

如果我们下凸包是介个样子的：

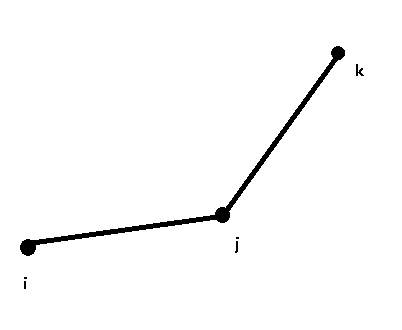
然后我们新加入了一个点 w：

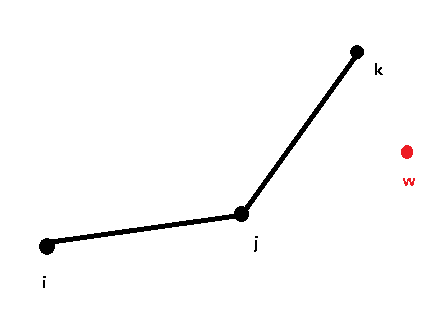
当我们连起了 k 和 w 时，发现斜率下降，变成了一个上凸包，那么根据上面我们总结的：“ 上凸包的中间点一定不是最优的 ” 这个性质，我们完全可是删掉点 k：

 

 

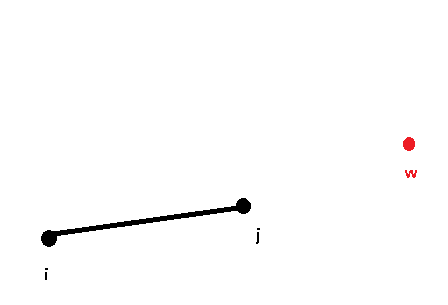
然后我们再连 j 和 w，发现还是个下凸包，那么就不用搞了：

 

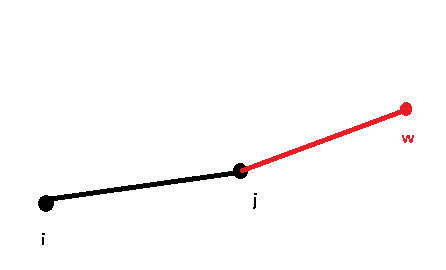
我们用单调队列来维护答案，每次加入一个决策点，如果发现会与之前的一些决策点形成斜率递减的三元组，那么删去中间的点；

每次队头就是答案；

代码实现：

 

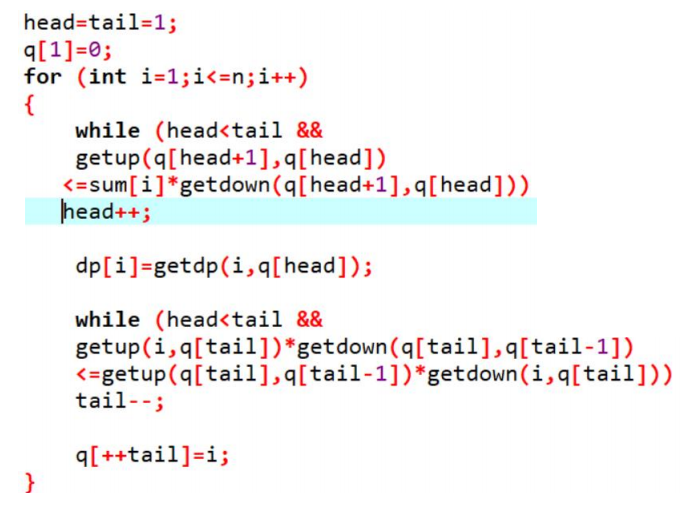
一模一样的练习题：bzoj3156

f [ i ] = min ( f [ j ] + ( i-j-1 ) * ( i-j ) / 2 + a [ i ] ) 。
设 k > j，且 k 优于 j 。
f [ k ] + ( i-k ) * ( i-k-1 ) / 2 + a [ i ] < f [ j ] + ( i-j ) * ( i-j-1 ) / 2 + a [ i ]； 
设 K = k+1，J = j+1，为了好推：

还是和上题一样单调队列维护一个 下凸壳即可。

 

 

总结

斜率优化其实就是一个优化 dp [ i ] = max / min { f [ j ] + g [ i ] * h [ j ] } + a [ i ] 式子的一个通用方法。

除了推式子的部分。

还要保证，推出来等式的右边要单调；不单调，就要在凸壳上二分。

等式左边抽象出来的点的 X 坐标也要单调，Y 坐标不需要保证单调。

当然其实 X 不单调和等式右边不单调也都能做，只不过难度较大，需要用到 CDQ 分治，或平衡树维护凸包的技巧。

 

常见模型

老套路了，排列计数问题考虑把数从小到大插入的过程进行 dp。 

设 f [ i ][ j ] 表示 1∼i 的排列，有 j 组相邻的相差1，且 i 和 i−1 不相邻的方案数； 

设 g [ i ][ j ] 表示 1∼i 的排列，有 j 组相邻的相差1，且 i 和 i−1 相邻的方案数。 

那么考虑插入 i+1 的位置，有： 

1. 不破坏空位且不与 i 相邻

2. 不破坏空位且与 i 相邻

3. 破坏空位且不与 i 相邻

4. 破坏空位且与 i 相邻（只发生在 g 的转移）4种。 

若我们将 i 插到 i-1 的旁边，则相邻数 +1；

若我们将 i 插到一对相邻数中，则答案 -1；

（特别的，如果 i-2 和 i-1 相邻且我们将 i 插到 i-2 和 i-1 之间，那么相邻数不变）；

其他插法的话相邻数不变；

分别推一下方案数即可。 

最后的答案就是 f [ n ][ 0 ] 。 

时间复杂度 O ( n² ) 。 

 

 

连通图计数套路：用总数减去不连通的方案数，而不连通的方案数，可以枚举 1 号点所在连通块的点集（有的问题中是大小），用这个点集的连通方案数乘以剩余点集的总方案数即可。 

g [ s ] 表示 s 点集互相连的所有情况（包括不连边的情况），就是把内部的 C 全乘起来；

f [ s ] 表示 s 状态下的合法情况，即使得 s 状态下所有点连通的合法情况。

答案是 f [ 2ⁿ - 1 ] 。 

g [ s ] 好求，考虑如何求 f [ s ]，f [ s ] 就是 g [ s ]（所有情况）减去所有的不合法情况 。

任意一个不合法的情况一号点肯定在某个联通块内，我们枚举不合法情况 1 号点所在的联通块的点集 i，那么这里不合法的情况就是 g [ s ^ i ] * f [ i ]，我们减去这些情况，就能求出 f [ s ] 了。

时间复杂度 O ( 3ⁿ )，也是要枚举子集 。

g 预处理可以做到 n * 2ⁿ 。

我们枚举一号点所在的集合：

假设一号点在 T 集合，那么剩下的点的集合 s^T 是不连通的；

那么 s 合法的方案数 =s 总的方案数  -  T 合法的方案数 * s^T 集合内随便连的方案数（不合法的方案数）；

为什么这样搞呢？在此特别鸣谢sy大佬的详细解释

我们已经将 s 分成两个子集 T 和 s^T 了，1 号点所在的集合肯定是要联通的，那么怎么才能保证这两个子集不连通呢？

其实发现我们只要不考虑两个子集之间的边不就OK了？这样打死也不连通！

那么这样的话 s^T 不就没有限制了？随便连就好了。

f [ s ] = g [ s ] - Σ（T∈ s ，T ≠ s，s 的最低位 ∈ T（包含 1 号点））f [ T ] （要联通）* g [ s^T ]（随便连）；

 

今天下午是杨思祺老师的讲授~

 

图论

图的基本模型

图的基本模型 图是点和边组成的集合体，G < V, E > 

V 是点集， E 是边集；

图的基本概念

有向边，有向图；

无向边，无向图；

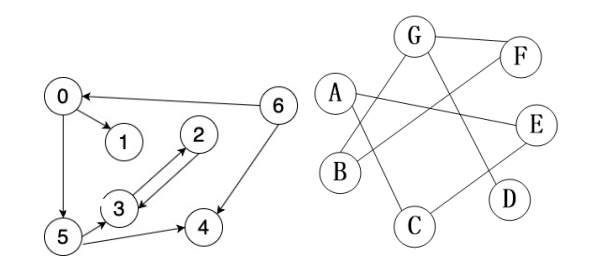
无权：没有权值；

点权：结点上的权值；

边权：边上的权值；

负权：权值为负数的情况；

环：图中的回路；

自环：从一个点出发连一条指向自己的边，形成了自环；

重边：两个点之间有多条直通路径；

有向无环图：有向无环图指的是一个无回路的有向图；

路径：两个点之间所经过的边；

简单路径：没有经过重复的点的路径；

联通：两个点之间能互相到达，如果一个图内任意两点都能互相到达，那么这个图是联通图；

树：包含 n 个点，n-1 条边的联通图就是树；

完全图：若干的点，任意两点都有连边的图（无向图）；

竞赛图：连有向边的完全图；

仙人掌：图里可以形成环，对于每一条边，要么不构成环，至多只属于一个环的树；

 

 

图的输入方式

最常见的输入方式是用 1 − N 表示顶点，并逐行给出 M 条边所 连接的两点和边权大小。

N M

u₁ v₁ w₁

u₂ v₂ w₂

. . .

u_m v_m w_m

如果有点权，一般会用一行 N 个数表示每个点的权值大小。

p₁ p₂ . . . p_n

 

图的存储方式

邻接矩阵是最简单的图存储方式。

对于 N 个点的图，用 N × N 的二维数组记录两点之间是否有边相连，以及边权大小。

空间复杂度 O ( N² )

对于边不存在的情况，可能采用 ∞，也可能使用 0 或 −1 等等特 殊值，视具体情况而定。

对于有重边的情况，可能不能完整保留所有边的信息。

邻接表是更为常用的图存储方式。

对每个点 u 用不定长度数组或链表存储所有以其为起点形如 < u, v > 的边。

无向图双向边拆分为两条单向边。 

不定长数组 

链表

空间复杂度 O ( N + M ) 。 

 

 图的遍历方法

广度优先遍历 BFS 队列； 

深度优先遍历 DFS 栈；

 

广度优先遍历 BFS

用队列实现，按照一定顺序依次访问每个结点。 

创建一个包含起点的队列； 

取出队首结点，将相邻的未入队结点加入队列； 

重复上一步直到所有结点都被遍历过 适用于无权图上单源最短路问题。 

 

深度优先遍历 DFS

用栈（递归函数）实现，按照一定顺序依次访问每个结点。 

从起点 s 开始遍历； 

在遍历到 u 时，递归遍历所有未被访问的相邻结点 v； 

当遍历 s 的函数退出时，所有结点都被遍历；

 

BFS 和 DFS 是最基础的图的遍历方法，更多的遍历方法基 本都是基于此两者；

BFS 和 DFS 都可以用来判断图连通，或者求连通子图；

两者各有优劣，要根据实际情况选择；

结合搜索的知识 。

 

三种 dfs 序

前序遍历

中序遍历

后序遍历

给出前序遍历和中序遍历怎么写？

前序遍历的第一个数就是整棵树的根，我们在中序遍历里找到这个数，那么它左边的都是左子树，右边的都是右子树，然后我们再递归求；

 

看个题，例一：

给定一个有向图，边权为 1 或 2，求单源最短路。

题解：

不许用任何最短路算法，只能用 bfs 和 dfs （雾）；

稍微改写一下 BFS 即可。

创建三个集合，Q₀ 表示当前层，Q₁ 表示距离为 1 的层， Q₂ 表示距离为 2 的层，初始 Q₀ { s } , Q₁ = ∅, Q₂ = ∅ 

依次取出 Q₀ 中的点，将其邻点放入对应的 Q₁ 或 Q₂ 中 

Q₀ = Q₁，Q₁ = Q₂， Q₂ = ∅

注意一个点可能和当前层既有长度为 1 的边，又有长度为 2 的 边，应当将其加入 Q₁ 而非 Q₂。

 

例二：

给出一个有向图和起点 s，对每条边 < u, v > 回答，如果删去这 条边，从 s 到 v 的最短路长度是否会改变。

题解：

求出从 s 出发的单源最短路；

我们保留最短路上的边，剩下的边都删掉；

如果 d_v = d_u + 1，那么说明这条边在最短路上，我们保留；

在最短路图上，如果 v 的入度为 1，则该入边是从 s 到 v 的必经边，若删去则 v 的最短路长度会改变；

在最短路图上，如果 v 的入度大于 1，则删去任何一条入 边，v 的最短路长度都不会改变；

 

拓扑排序

有向无环图的拓扑排序即将所有顶点排为线性序列，使得对于任意的 < u, v > ∈ E，都有 u 在线性序列中出现于 v 之前。

有向图中如果有环，则一定不存在拓扑排序；如果没有环，则一 定存在拓扑排序。

做法：

选取一个入度为 0 的点记为 u ；

将 u 添加到线性序列末端 ；

删去所有 u 的出边 ；

重复上述步骤直到所有点都被加入序列；

 

例一：

有 n 项任务，有 m 个限制，第 i 个限制要求执行任务 u_i 之前必须要完成任务 v_i。请问是否存在合适的任务执行顺序，满足所有的限制。

题解：

将每个任务视为一个点，任务之间的依赖构成了有向边。如果该有向图中没有环，则存在拓扑排序，而拓扑排序就是可行的任务 执行顺序；如果该有向图中存在环，则无解。 

 

例二：

有 n 项任务，有 m 个限制，限制有如下两种： 

1. 执行 u 任务之前必须要完成 v 任务； 

2. 存在某一时刻，u 和 v 任务都在执行；

请问是否存在安排每个任务起始时间和结束时间的方案，满足所有的限制。

题解：

为每个任务的起始时间和结束时间各对应一个点，任务 i 的起始 时间点记为 s_i，结束时间点记为 e_i。

要保证每个任务的结束时间在起始时间之后，所以对所有 i， 连边 < s_i , e_i >

如果要求任务 a 在任务 b 开始执行之前完成，则连边 < e_a , s_b >

如果要求任务 a 和 b 在某个时刻都在执行，则连边 < s_a , eb >, < s_b , e_a >

对于上面的有向图，如果存在环则无解，否则根据其拓扑排序易构造一个方案。

 

例三：

对于带边权的有向无环图，求单源最短路。

题解：

记起点为 s，拓扑排序形如 a₁, a₂, . . . , a_t , s, b₁, b₂, . . . , b_k，记点 i 的最短路为：

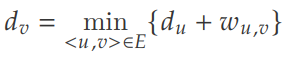
从 s 出发无法走到 a₁, a₂, . . . , a_t，对这些点其最短路为 ∞ ；

从 s 出发走到 b_i 之前一定只经过 b₁, b₂, . . . , b_i−1，即 d_bi 的求解依赖于 d_b1 , d_b2 , . . . , d_bi−1 ；

按顺序依次求解 d_s , d_b1 , d_b2 , . . . , d_bk 即可。

 

 

例四：

An ascending sorted sequence of distinct values is one in which some form of a less-than operator is used to order the elements from smallest to largest. For example, the sorted sequence A, B, C, D implies that A < B, B < C and C < D. in this problem, we will give you a set of relations of the form A < B and ask you to determine whether a sorted order has been specified or not.

由一些不同元素组成的升序序列是可以用若干个小于号将所有的 元素按从小到大的顺序排列起来的序列。例如，排序后的序列 为 A, B, C, D，这意味着 A < B、B < C 和 C < D。在本题中， 给定一组形如 A < B 的关系式，你的任务是判定是否存在一个有序序列。输出到哪一项可以确定顺序或者在这一项最先出现冲突，若所有的小于关系都处理完了都不能确定顺序也没有出现冲突，就输出不能确定。

题解：

冲突即为出现环；

如果拓扑排序的时候发现队列里的元素大于 1 了，那么就说明不能确定顺序；

每次加入新的关系重新拓扑排序一次即可；

 

BZOJ 2200 道路和航线

FJ 正在一个新的销售区域对他的牛奶销售方案进行调查。他想把牛奶送到 T 个城镇 (1 ≤ T ≤ 25000)，编号为 1 到 T。这些城 镇之间通过 R 条道路 (1 ≤ R ≤ 50000) 和 P 条航线 (1 ≤ P ≤ 50000) 连接。每条道路 i 或者航线 i 连接城镇 Ai 到 Bi，花费为 C_i。对于道路，0 ≤ C_i ≤ 10000; 然而航线的花费很神奇，花费 C_i 可能是负数 (−10000 ≤ C_i ≤ 10000)。道路是双向的，可以从 A_i 到 B_i，也可以从 B_i 到 A_i，花费都是 C_i。然而航 线与之不同，只可以从 A_i 到 B_i。事实上，由于最近恐怖主义太嚣张，为了社会和谐，出台了一些政策保证：如果有一条航线可以从 A_i 到 B_i，那么保证不可能通过一些道路和航线从 B_i 回到 A_i。由于 FJ 的奶牛世界公认〸分给力，他需要运送奶牛到每一 个城镇。他想找到从发送中心城镇 S 把奶牛送到每个城镇的最便宜的方案，或者知道这是不可能的。

题解：

注意到如果有一条航线可以从 A_i 到 B_i，那么保证不可能通过一 些道路和航线从 B_i 回到 A_i。 换言之，不存在包含航线（负权单向边）的环。

首先加入所有正权无向边，找出所有连通块，每个连通块缩为一 个点。

再加入所有单向边，此时图一定为 DAG。

在 DAG 上用 BFS 更新最短路，在正权无向边组成的连通块 （缩点）内部使用 Dijkstra 更新最短路。

 

最短路算法

全局最短路： Floyd ；

单源最短路： Dijkstra， SPFA， Bellman-Ford；

 

Floyd

基于动态规划，F_k,u,v ，表示使用点 1, 2, . . . , k 时，点 u 到点 v 的最短路 ；

从小到大枚举 k，u 和 v 之间的最短路要么不经过 k，要么 经过 k 一次且除此之外只包含前 k − 1 个点；

易见，使用二维数组不断覆盖更新即可。 时间复杂度 O(N³ ) ，空间复杂度 O(N² ) ，可以处理含有负权边的情况，如果含有负环，则存在 i 使得 F_i,i < 0 。

但是空间开三维有点奢侈，我们可以减去 k 的那一位，缩减成为二维的。

 

 

传递闭包

问图上任意两点的可达性。

 

Dijkstra

适用于没有负权边的图。 

将所有点分为两个集合，最短路确定的集合 S 和最短路未确定的集合 T，初始 S { s }； 

求 T 中每个点 v 的当前最短路；

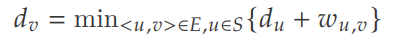
取出 T 中 d_v 最小的点，其最短路一定就是 d_v，将其加入 S ；

不断重复上面的操作，直到所有点的最短路都确定朴素写法时间复杂度较劣，可以采用堆优化至 O ( (N + M) log N )；

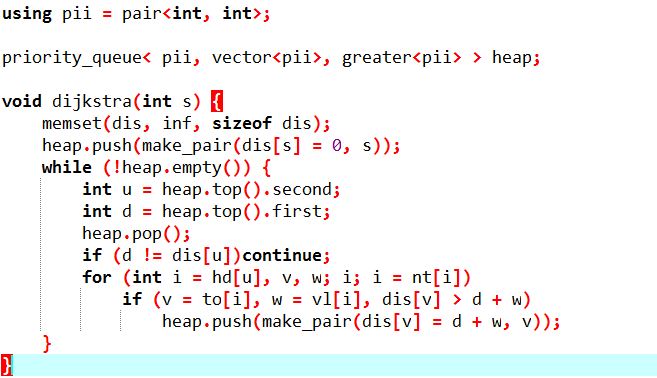
用 pair 的毒瘤代码： 

 

用结构体的友好代码：

 

 

Bellman-Ford

初始令 d_s = 0，其余 d_i = ∞ ；

依次使用每一条边 < u, v > 更新，dv =  min { d_v , d_u + w_u,v } ；

不断循环直到所有 d_i 都不会更新 ；

因为任何一条最短路包含至多 n − 1 条边，没有负环则不超 过 n 轮就会停止 ；

时间复杂度 O (NM)， 空间复杂度 O (N + M)；

可以对包含负权边的图使用，如果存在负环，则循环超过 n 轮后依然不会停止，可以用来判断负环是否存在。

 

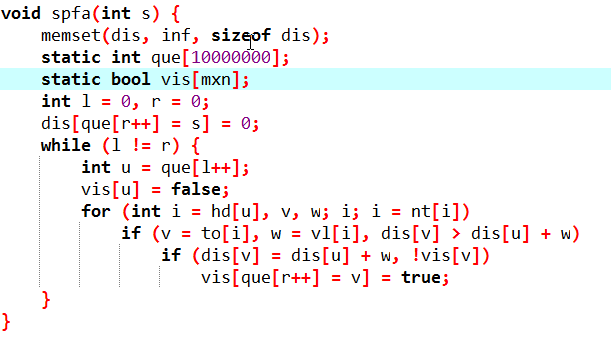
SPFA

考虑使用队列优化 Bellman-Ford 算法，如果更新了 d_u，则将 u 入队。每次取队首 u 更新其邻点 v 的 d_v 。

最坏情况会被卡到 O（NM）；