P4001 [ICPC-Beijing 2006]狼抓兔子
原题链接 https://www.luogu.org/problem/P4001


恩,这是一道最小割的问题~
那么为什么会在最短路的标签里呢?那就是利用了一个性质:
平面图的最小割等于其对偶图的最短路!
所以我们将题目给出的图转化成其对应的对偶图再跑一遍最短路就做完了!
难想就难想在怎么建对偶图这个问题上。
重点讲一讲怎么建对偶图:
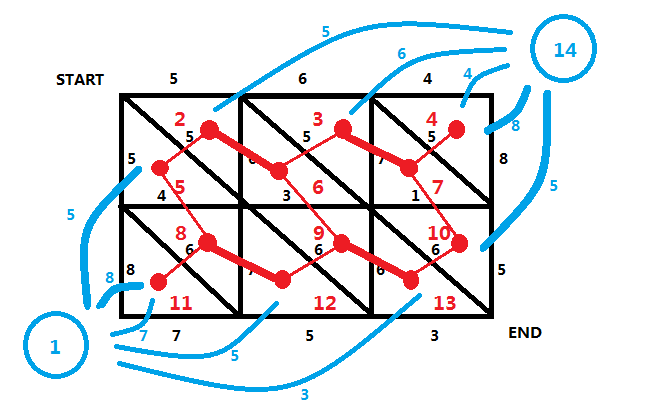
我们将图中的每个三角形抽象看成一个点(红点):
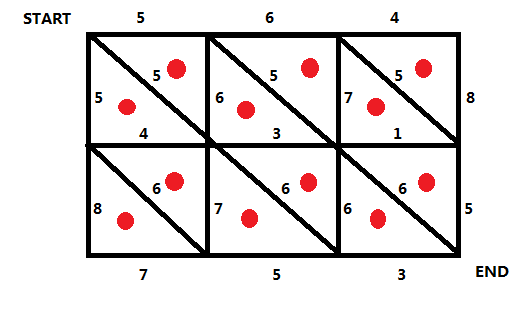
然后我们在左下角和右上角各设置一个点,我们将与这两个点相邻的边上的所有红点连起来(注意连双向边),这个边的权值就是连接红点时穿过的边的权值(红点之间也要玄学得连起来,但是注意要对偶):
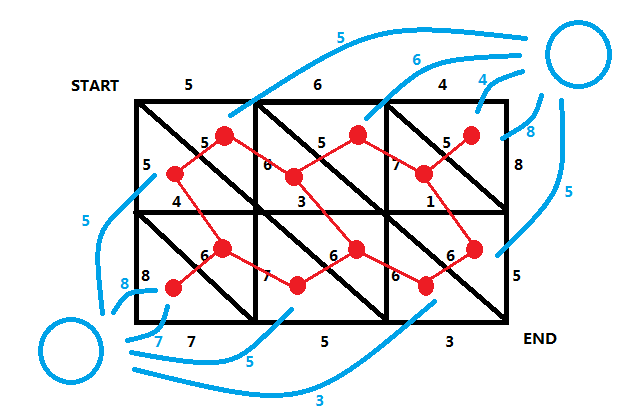
我们画出来对偶图之后,这个题就基本解决了,我们自己手动走一遍就可以知道:在对偶图中我们从我们设的这个左下角的点走到右上角的点的任意一条路径,删去路径上所有经过的边,都是一个割!而这条路径上每条边的和就是这个割的值;
那么我们的问题就转化成:在这个对偶图上跑一遍最短路就好了,求出的就是最小割。
说的轻松,代码还是不会写啊QwQ~
代码实现
我们将左下角这个虚点的编号设为 1,然后从左往右从上往下挨个给每个红点标号,最后再给右上角的虚点标号:
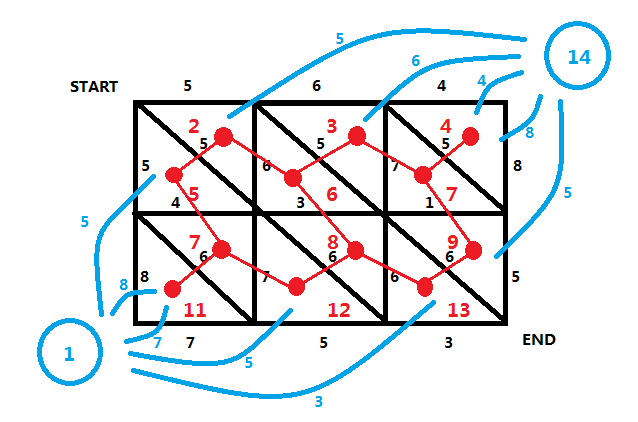
然后我们找规律:
1. 对于横着的边,第 1 行的被下面的点和右上角虚点所连的边穿过,第 n 行的被上面的点和左下角虚点所连的边穿过,其余的被上面和下面的点穿过;
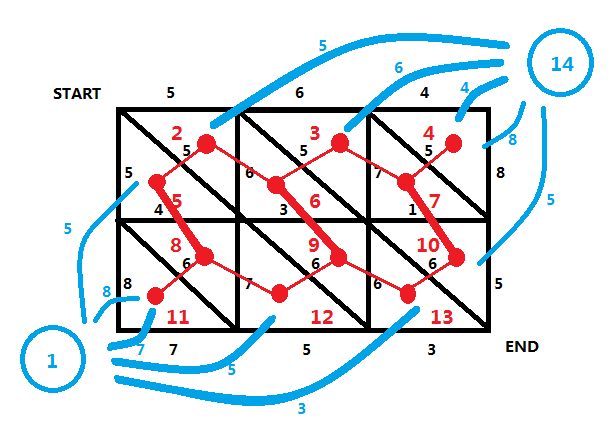
下边的点的编号:under = ( i - 1 ) * ( m - 1 ) * 2 + j + 1;
上边的点的编号:on = under - ( m - 1 );
for(int i=1;i<=n;i++) //横着的边 { for(int j=1;j<=m-1;j++) { w=read(); under=(i-1)*(m-1)*2+j+1; //下边的点的编号 on=under-(m-1); //上边的点的编号 if(i==1) add(under,en,w),add(en,under,w); else if(i==n) add(st,on,w),add(on,st,w); else add(under,on,w),add(on,under,w); }
2. 对于竖着的边,第 1 列的被右面的点和左下角虚点所连的边穿过,第 n 列的被左面的点和右上角虚点所连的边穿过,其余的被左面和右面的点穿过;
左边的点的编号:l = ( i - 1 ) * ( m - 1 ) * 2 + j;
右边的点的编号:r = l + m;
for(int i=1;i<=n-1;i++) //竖着的边 { for(int j=1;j<=m;j++) { w=read(); l=(i-1)*(m-1)*2+j; //左边的点的编号 r=l+m; //右边的点的编号 if(j==1) add(st,r,w),add(r,st,w); else if(j==m) add(l,en,w),add(en,l,w); else add(l,r,w),add(r,l,w); } }
3. 对于斜着的边,将左面和右面的的点连起来就好了;
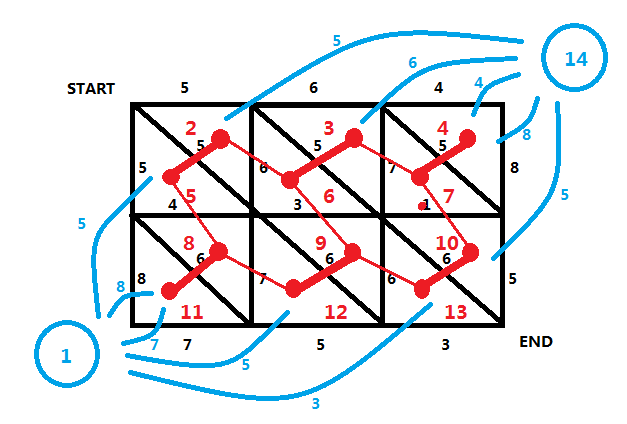
右边的点的编号:r = ( i - 1 ) * ( m - 1 ) * 2 + j + 1;
左边的点的编号:l = r - ( m - 1 );
for(int i=1;i<=n-1;i++) //斜着的边 { for(int j=1;j<=m-1;j++) { w=read(); r=(i-1)*(m-1)*2+j+1; //右边的点的编号 l=r+(m-1); //左边的点的编号 add(l,r,w); add(r,l,w); } }
然后建完边跑一遍 Dijkstra 就做完啦,完整代码如下:
#include<iostream> #include<cstdio> #include<queue> using namespace std; int read() { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } const int inf=1e8; int n,m,on,w,under,l,r,edge_sum,st,en,head[2000100],vis[2000101],dis[2000101]; struct node { int dis,pos,from,to,next; bool operator < (const node &x)const //重载小于号 { return x.dis<dis; } }a[7000001]; priority_queue<node> q; void add(int from,int to,int dis) { edge_sum++; a[edge_sum].next=head[from]; a[edge_sum].from=from; a[edge_sum].to=to; a[edge_sum].dis=dis; head[from]=edge_sum; } void Dijkstra() //跑最短路(堆优化) { for(int i=1;i<=en;i++) dis[i]=inf; dis[st]=0; q.push((node){0,1}); while(!q.empty()) { node u=q.top(); q.pop(); if(vis[u.pos]) continue; vis[u.pos]=1; for(int i=head[u.pos];i;i=a[i].next) { int zd=a[i].to; if(dis[zd]>dis[u.pos]+a[i].dis) { dis[zd]=dis[u.pos]+a[i].dis; q.push((node){dis[zd],zd}); } } } } int main() { n=read();m=read(); st=1;en=(n-1)*(m-1)*2+2; for(int i=1;i<=n;i++) //横着的边 { for(int j=1;j<=m-1;j++) { w=read(); under=(i-1)*(m-1)*2+j+1; //下边的点的编号 on=under-(m-1); //上边的点的编号 if(i==1) add(under,en,w),add(en,under,w); else if(i==n) add(st,on,w),add(on,st,w); else add(under,on,w),add(on,under,w); } } for(int i=1;i<=n-1;i++) //竖着的边 { for(int j=1;j<=m;j++) { w=read(); l=(i-1)*(m-1)*2+j; //左边的点的编号 r=l+m; //右边的点的编号 if(j==1) add(st,r,w),add(r,st,w); else if(j==m) add(l,en,w),add(en,l,w); else add(l,r,w),add(r,l,w); } } for(int i=1;i<=n-1;i++) //斜着的边 { for(int j=1;j<=m-1;j++) { w=read(); r=(i-1)*(m-1)*2+j+1; //右边的点的编号 l=r+(m-1); //左边的点的编号 add(l,r,w); add(r,l,w); } } Dijkstra(); printf("%d",dis[en]); return 0; }


