7月清北学堂培训 Day 5
今天是钟皓曦老师的讲授~
动态规划
动态规划的三种实现方法:
1.递推;
2.递归;
3.记忆化;
举个例子:
斐波那契数列:0,1,1,2,3,5,8……
Fn = Fn-1 + Fn-2
1.我们直接递推,用别人的结果得到自己的结果:
#include<iostream> using namespace std; int main() { cin >> n; f[0]=0;f[1]=1; for (int a=2;a<=n;a++) f[a] = f[a-1] + f[a-2]; cout << f[n]; return 0; }
2.用自己的结果去算其他的结果:
#include<iostream> using namespace std; int main() { cin >> n; f[0]=0;f[1]=1;for (int a=0;a<n;a++) { f[a+1] += f[a]; f[a+2] += f[a]; } return 0; }
在动态规划的时候,任何一个题都可以用这两种方法去写;
但是不同的题对两种方法有优有劣,所以我们两种方法都要会。
3.记忆化搜索:
我们很容易发现求斐波那契数列的过程就是递归的过程,那么就可以写一下递归的代码:

由于我们这种方法的斐波那契数是一个一个加上去的,时间复杂度是O(Fn);
如果一个东西已经被算出来了,那么我们就把它存下来,以后直接访问就好了,不用再递归,这就是记忆化搜索:
int f[233]; bool g[233]; int dfs(int n) { if (n==0) return 0; if (n==1) return 1; if (g[n]) return f[n]; f[n] = dfs(n-2) + dfs(n-1); g[n]=true; return f[n]; }
动态规划具有的特点:
状态:要算算什么;
转移方程:要怎么算;
无后效性:动态规划所有的状态之间组成的有向无环图;
阶段性:我们在求一个状态时,前面的状态一定是已经求出来的;
有时候动态规划不一定是从1 -> n 的,它可能是乱序的;但我们要始终记住它是一个 DAG,所以可以将每个状态看作一个结点,进行拓扑排序,然后就又变得有序了;
动态规划的常见种类:
1.背包问题:
01背包:
n 个物品,m 容量,每个物品有体积和价值,放入的物品不超过背包容量,求最大化价值和;
第一个维度:f [ i ] 表示我们现在已经放好了前 i 个物品了;
第二个维度:f [ j ] 表示放进去的物品的体积之和是多少;
那么状态就是:f [ i ][ j ] 代表我们已经尝试将前 i 个物品都放进去过,体积之和为 j 时所能取到的最大价值;
怎么转移?
如果第 i+1 个物品不放进去: f [ i ][ j ] = f [ i+1 ][ j ] ;
如果第 i+1 个物品放进去:f [ i+1 ][ j+v[i+1] ] = f [ i ][ j ] + w [ i+1 ];
这种方法是自己更新别人。
我们现在用别人更新自己:
如果第 i 个物品不放进去:f [ i ][ j ] = f [ i-1 ][ j ];
如果第 i 个物品放进去:f [ i ][ j ]= f [ i-1 ][ j-v[i-1] ] + w[ i ];
注意边算边取 max;
#include<iostream> #include<cmath>
using namespace std; int n,m,w[233],v[233]; int f[233][233]; int main() { cin >> n >> m; for (int a=1;a<=n;a++) cin >> v[a] >> w[a]; for (int i=1;i<=n;i++) for (int j=0;j<=m;j++) { f[i][j] = f[i-1][j]; if (j >= v[i]) f[i][j] = max(f[i][j],f[i-1][j-v[i]]+w[i]); } int ans=0; for (int a=0;a<=m;a++) ans = max(ans,f[n][a]); cout << ans << endl; return 0; }
完全背包:
考虑每个物品可以用无限次的最大价值。
状态还是不变。
重新考虑下状态转移方程:
由于每个物品可以放若干个,所以我们枚举一下第 i 个物品放了多少个;
#include<iostream> using namespace std; int n,m,w[233],v[233]; int f[233][233]; int main() { cin >> n >> m; for (int a=1;a<=n;a++) cin >> v[a] >> w[a]; for (int i=1;i<=n;i++) for (int j=0;j<=m;j++) for (int k=0;k*v[i]<=j;k++) //注意上限 f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]); int ans=0; for (int a=0;a<=m;a++) ans = max(ans,f[n][a]); cout << ans << endl; return 0; }
但是时间复杂度升到了O(n3),我们要考虑一下优化:
我们可以在之前01背包的代码上做个小小的改动就好了:
#include<iostream> #include<cmath> using namespace std; int n,m,w[233],v[233]; int f[233][233]; int main() { cin >> n >> m; for (int a=1;a<=n;a++) cin >> v[a] >> w[a]; for (int i=1;i<=n;i++) for (int j=0;j<=m;j++) { f[i][j] = f[i-1][j]; if (j >= v[i]) f[i][j] = max(f[i][j],f[i][j-v[i]]+w[i]); //改动就是这里 } int ans=0; for (int a=0;a<=m;a++) ans = max(ans,f[n][a]); cout << ans << endl; return 0; }
为什么这样是对的呢?原理何在?
我们可以简单地画一下这个程序的流程图:
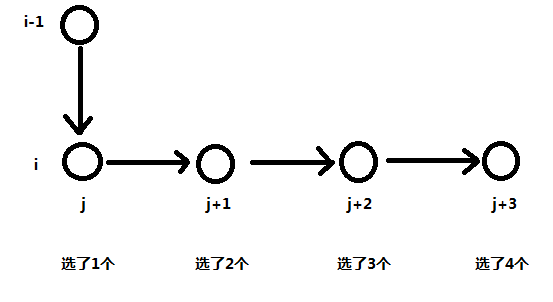
我们改动之后的那一行的代码的意思就是在第 i 层上横着跑,每走一次就是第 i 种物品在原先的基础上多选一个,无限走下去就实现了选无限个物品;
这样时间复杂度就被我们降到了O(n2);
有限背包:
考虑每个物品可以用有限次的最大价值。
我们直接枚举每个物品用多少次:
#include<iostream> #include<cstdio> #include<cmath> using namespace std; int n,m,w[233],v[233],z[233]; int f[233][233]; int main() { cin >> n >> m; for (int a=1;a<=n;a++) cin >> v[a] >> w[a] >> z[a]; for (int i=1;i<=n;i++) for (int j=0;j<=m;j++) for (int k=0;k<=z[i];k++) f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]); int ans=0; for (int a=0;a<=m;a++) ans = max(ans,f[n][a]); cout << ans << endl; return 0; }
时间复杂度O(n3)级别的,显然不行,考虑优化一下:
我们可以将原先的物品捆绑在一起:
假设我们一个物品能用 13 次,那么我们就可以将这 13 个拆成四个捆绑包:

假设我们要选 9 个这种物品,其实就是选上第1,2,4 个捆绑包!
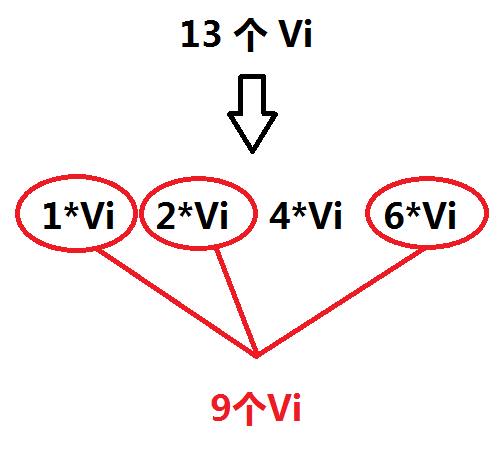
这样的话,我们原先的有限背包的问题就转化成了01背包的问题!(判断选择那几个捆绑包)
时间复杂度O(n2k),k 是物品能分成几个捆绑包;
怎么拆捆绑包?类似于二进制:
如果我们一个物品能用 26 次:
我们可以将 26 拆成:1,2,4,8……,我们接下来要拆 16 了,可是只剩下了 26-1-2-4-8=11,明显小于 16,所以最后一个包的大小就是11;
为什么要这样拆分捆绑包呢?换句话说就是为什么这样能包含所有的情况呢?
最终的疑问还是在最后一个捆绑包11上。
我们看 26 能拆成的所有捆绑包:1,2,4,8,11;
由于前四个数是我们通过二进制分解来的,所以前四个捆绑包能表示1~15的所有情况;
那么对于16~26的情况呢?这时候我们就必须选上最后一个捆绑包11,那么我们还需选5~15,这不就转化成了前面的情况了嘛?明显5~15能被前四个捆绑包全部包含。
证毕!
我们发现拆成的捆绑包的个数是 log n,那么时间复杂度就是:O(nm log n);
我们在读入的时候就要处理一下捆绑包。
#include<iostream> #include<cmath> using namespace std; int n,m,w[233],v[233]; int f[233][233]; int main() { cin >> n >> m; int cnt = 0; for (int a=1;a<=n;a++) { int v_,w_,z; cin >> v_>> w_ >> z; //z个物品 int x = 1; while (x <= z) //如果能分解出一个完整的捆绑包就分解 { cnt ++; //捆绑包个数加一 v[cnt] = v_*x; //这个捆绑包的体积 w[cnt] = w_*x; //这个捆绑包的价值 z-=x; //还剩下多少个物品 x*=2; //别忘记乘2 } if (z>0) //如果有剩余,单独作为最后一个捆绑包 { cnt ++; v[cnt] = v_*z; w[cnt] = w_*z; } } n=cnt; //改成捆绑包的数量 for (int i=1;i<=n;i++) //和01背包的代码一样 for (int j=0;j<=m;j++) { f[i][j] = f[i-1][j]; if (j >= v[i]) f[i][j] = max(f[i][j],f[i-1][j-v[i]]+w[i]); } int ans=0; for (int a=0;a<=m;a++) ans = max(ans,f[n][a]); cout << ans << endl; return 0; }
2.基础动态规划
经典例题:数字三角形
状态:f [ i ][ j ] 走到第 i 行第 j 列所经过的最大数字之和最大是多少;
考虑到 f [ i ][ j ] 要么从上面 f [ i-1 ][ j ] 走过来,要么从左上方 f [ i-1 ][ j-1 ] 走过来,所以取个max就好了;
状态转移方程: f [ i ][ j ] = max ( f [ i-1 ][ j ] , f [ i-1 ][ j-1 ] ) + a [ i ][ j ];
数字三角形2
由于太简单,加了一个条件:求最后答案 mod 100 最大。
如果我们还是像刚才那样定义状态的话是错的,因为和大的话不一定模数最大,也就是说前面的最优值不能求出后面的最优值;
这个题多一个条件,那么我们就增加一个维度;
定义状态: f [ i ][ j ][ k ] 我们走到第 i 行第 j 列的位置使得最大值之和模 100 等于 k 是可行不可行的;
状态转移方程:
从 ( i , j ) 往下走:f [ i+1 ][ j ][ (k+a[ i+1 ][ j ])%100 ] =1;
从 ( i , j ) 往右下走:f [ i+1 ][ j+1 ][ (k+a[ i+1 ][ j+1 ])%100 ] =1;
初始化:f [ 1 ][ 1 ][ a[1][1]%100 ] = 1;
#include<iostream> using namespace std; bool f[233][233][233]; int main() { cin >> n; for (int i=1;i<=n;i++) for (int j=1;j<=i;j++) cin >> a[i][j]; f[1][1][a[1][1] % 100] = true; for (int i=1;i<n;i++) for (int j=1;j<=i;j++) for (int k=0;k<100;k++) if (f[i][j][k]) { f[i+1][j][(k+a[i+1][j])%100]=true; f[i+1][j+1][(k+a[i+1][j+1])%100]=true; } for (int j=1;j<=n;j++) for (int k=0;k<100;k++) if (f[n][j][k]) ans=max(ans,k); cout << ans << endl; return 0; }
最长上升子序列
状态设置:f [ i ] 表示 i 这个数最为最后一个数时最长上升子序列的长度;
f [ i ] = max ( f [ j ] + 1 ),1 <= j <= i 且 aj < ai ;
枚举 j 的时候我们可以用线段树;
用数据结构来加速动态规划求值是个常用的方法;
3.区间动态规划
经典例题:合并石子
有 n 堆石子,每次只能合并相邻两堆石子,花费的代价是两堆石子的重量和,求将 n 堆石子合并成 1 堆石子的最小代价;
状态设置:f [ i ][ j ] 表示将第 i 堆石子合并到第 j 堆石子的最小代价;
初始化:f [ i ][ i ] = 0,把自己合并到自己的代价是0;
状态转移方程:
我们一定可以找到一个分界线,使得先使分界线左边的所有石子合并成一堆,分界线右边的所有石子合并成一堆,最后将两堆石子再合并;
所以我们可以枚举一个中界线 k,左边的答案就是 f [ i ][ k ],右边的答案就是 f [ k+1 ][ j ],那么 f [ i ][ j ] = min ( f [ i ][ k ] + f [ k+1 ][ j ] + i~j的区间和 ),区间和的话前缀和就可以维护;
最后的答案就是 f [ 1 ][ n ](把第一堆石子合并到第 n 堆石子);
详细请看之前我整理的博客(雾 【传送门】
我们第一个维度应该要枚举长度:
如果我们是按照左端点从 1~n 枚举作为第一维度的话,假如我们要求 f [ 1 ][ n ],我们应该是用 f [ 1 ][ i ] + f [ i+1 ][ n ] 来更新答案的,那么,f [ i+1 ][ n ] 算出来了嘛?显然没有!因为我们的左端点从小到大,现在才枚举到1呢,i 肯定还没有被更新,所以这是错的!所以我们按照区间长度来枚举作为第一维是对的:一个长度为 i 的区间一定是由两个长度小于 i 的区间来更新的,这样就可以了。
#include<iostream> #include<cstdio> #include<cmath> using namespace std; int read() { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } int n,a[201],fminx[201][201],fmaxn[201][201]; long long sum[201]; int main() { n=read(); for(int i=1;i<=n;i++) { a[i]=read(); a[n+i]=a[i]; } for(int i=1;i<=n*2;i++) { sum[i]=sum[i-1]+a[i]; fminx[i][i]=0; fmaxn[i][i]=0; } for(int i=2;i<=n;i++) //枚举区间长度 { for(int j=1;i+j<=2*n+1;j++) //枚举区间左端点 { int r=i+j-1; fmaxn[j][r]=0; fminx[j][r]=1e9; for(int k=j;k<r;k++) { fmaxn[j][r]=max(fmaxn[j][k]+fmaxn[k+1][r],fmaxn[j][r]); fminx[j][r]=min(fminx[j][k]+fminx[k+1][r],fminx[j][r]); } fmaxn[j][r]+=sum[r]-sum[j-1]; fminx[j][r]+=sum[r]-sum[j-1]; } } int minx=1e9,maxn=-1e9; for(int i=1;i<=n;i++) { minx=min(minx,fminx[i][i-1+n]); maxn=max(maxn,fmaxn[i][i-1+n]); } printf("%d\n%d",minx,maxn); return 0; }
矩阵乘法
计算 n 个矩阵的矩阵乘法,自定义运算顺序,问最少需要几次运算?
两个矩阵相乘后,就会产生一个新矩阵,所以就是矩阵合并。
状态定义:f [ l ][ r ] 表示将第 l 个矩阵乘到第 r 个矩阵需要多少次;
状态转移方程: f [ l ][ r ] = min ( f [ l ][ k ] + f [ k+1 ][ r ] + al * ak+1 * ar+1 ), l <= k <= r;
代码参考石子合并那个题。
4.状态压缩动态规划
按照选取集合的状态划分转移阶段;
转移方式:枚举下一个要选取的物品。
看个例题:
平面设计有 n 个点,每个点的坐标是(xi , yi ),问从一号点走完所有点最后再回到一号点的最短路径。
首先每个点没有必要走两次,走一次就够了。
变化量:
1.当前在哪个点;
2.走过哪些点(我们需要从没走过的点里面选一个走);
状态设置:f [ s ][ i ] 我现在走到了第 i 个点,走过了哪些点(s);
但是走过哪些点怎么用一个整数表示?
我们就要用到了状态压缩:把一个数组压缩成一个数。
假设我们有五个点:
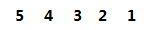
情况是:我们已经走了1,2,4 这三个结点了,3,5结点还没有走:

我们将走过的结点的位置写上1,未走过的结点的位置写上0:
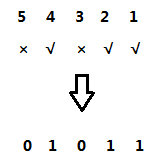
我们可以将下面这个01串看做是一个二进制的数,然后我们再将其转化成十进制的数:
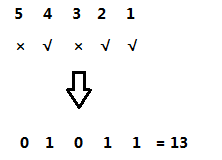
这样的话,我们就将这种情况转化成了一个数字,这就是状态压缩。
边界条件:
f [ 1 ][ 0 ] = 0,我只走了第 0 个点(1只有第0位有1),当前位置在0,时间是0;
状态转移方程:
我们找个没走过的点走一下就好了。
枚举一个 j,看看 s 的二进制的第 j 位是不是0,如果是0就走 j ,并把第 j 位改成 1;
注意要先枚举状态在枚举每个点,因为我们走的点是越来越多的;
#include<iostream> #include<cmath> #include<cstring> using namespace std; const int inf=1e9; double f[233333][233]; double x[233],y[233],ans; int n; double dis(int a,int b) { return sqrt((x[a]-x[b])*(x[a]-x[b])+(y[a]-y[b])*(y[a]-y[b])); } int main() { cin >> n; for (int a=0;a<n;a++) cin >> x[a] >> y[a]; memset(f,0x3f,sizeof(f)); //初始化无穷大 f[1][0]=0; //边界条件 for (int s=0;s<(1<<n);s++) //枚举每种状态 for (int i=0;i<n;i++) //枚举当前结点是哪个数 if (f[s][i] < inf) { for (int j=0;j<n;j++) //枚举哪个数没去过 if ( ((s>>j) & 1) == 0) //如果s的第j位是0,说明没去过 { int news = s | (1<<j);//新的状态:将s的第j位变成1 f[news][j] = min(f[news][j],f[s][i] + dis(i,j)); //更新 } } for (int i=0;i<n;i++) ans=min(ans, f[(1<<n)-1][i] + dis(i,0));//枚举每个终点,然后记得要返回0号结点 cout << ans; return 0; }
这类问题是旅行商问题(TSP问题),时间复杂度最优为O(2n * n2),能用状压DP的话数据要在 n <= 22 的范围内;

在一个种草之后,与之相邻的四个格子都不能种草了;
状态定义:f [ i ][ s ] 表示前 i 行的草已经种完了,且第 i 行种的草的长相是 s;
状态转移方程:
前 i 行已经种完草了,我们考虑第 i+1 行怎么种草;
第 i+1 行不能连着种草。所以用二进制表示的时候不能有两个连续的两个1,由于相邻的两列也不能种草,所以第 i 行种草的地方第 i+1 行不能种草。
假设我们第二行的种植情况是这样的:

由于相邻的格子不能种植,所以我们可以确定第 i+1 行一定不能种在这些格子上:
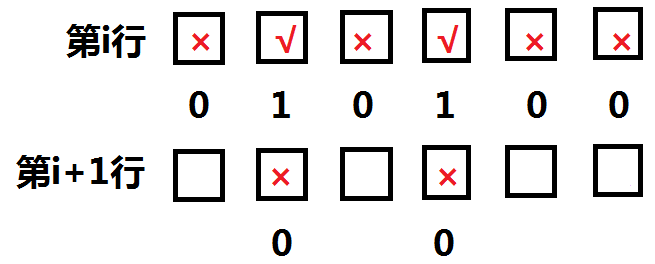
其他的位置问你不能确定,但是我们可以发现一个规律:si & si+1 = 0。
所以我们只要先找一个s',使得 s & s' = 0 就行了;

发现和上一个题没有什么本质的区别,只是多了个条件;
题目多一个条件直接多加一个维度:
状态定义:f [ i ][ s ][ j ] 第 i 行的国王已经放完了,已经放了 j 个国王的情况下,第 i 行国王放置的情况为 s;
相比于上个题来说只是再需要判断一下对角线上也不能放国王就好了。
5.数位动态规划
什么是数位DP?
数位DP 是我们在 DP 的时候是按照数的每一位来进行转移的动态规划;
给出两个数 l , r,问从 l~r 有多少个数。
显然答案就是:r - l + 1;
但是我们要用数位DP 做!
首先数位DP有个叫前缀和转化的东西:算[ l , r ] 有多少个数,就是算 [ 0 , r ] 里有多少个数 - [ 0 , l-1 ] 里有多少个数;
那么问题就转化成求 [ 0 , x ] 有多少个数。
假设 x = 3245,
实际上就是在问有多少个 y ,使得 0 <= y <= x;
考虑到 x 只有四位,那么 y 最多也只有四位。
也就是说,我们要往四个格子里面填数,问有多少种方案使得填出来的数小于等于 x;
如果从低位往高位填的时候并不知道是否比 x 大还是小,但我们往高位往低位填的时候就能确定了。
状态设置:f [ i ][ j ] 我们在第 i 位已经填好的情况下,如果 j = 0 代表我们填的数已经小于x,如果 j = 1 代表我们填的数无法确定是等于还是大于,考虑到我们不用算大于的情况,所以 j = 1 代表我们填的数刚好等于 x;
状态转移方程:
假设我们已经填好了第 i 位,我们接下来要填的是第 i-1 位(从高往低填),数位DP 的过程就是在求我们这一位是填1~9的哪一位;
初始化:f [ l+1 ][ 1 ] = 1;
我们的 x 只有 l 位,那么我们 l 位的更高位一定是0,所以与 x 一样的方案数有1种:全部填0;
判定一下将 k 填进去之后会不会比 x 大:
1.如果前几位都一样,当时当前填的 k 比 x 的对应位大的话,那么我们不转移;否则如果小于的话,那么第二维是0,如果正好又等于 x,那么第二维继续维持 1:
2.如果之前的数就比 x 小了,那么之后不管怎么填始终是小于 x 的,也就是说我们的第二维仍然是0;

最后的答案就是: f [ 1 ][ 0 ] + f [ 1 ][ 1 ];

还是数位 DP 前缀和的思想:求 [ 0 , r ] 的数的数位之和 - [ 0 , l-1 ] 的数的数位之和;
状态设置:g [ i ][ j ] 我们填好第 i 位后,是等于还是小于的数字之和;
假设我们在一位填了一个 k,每种方案都接了一个 k,填 k 的总贡献就是:f [ i ][ j ] * k;
所以我们不仅要求所有数的数位之和,还要求方案数,那么我们在上面代码的基础上改一改就好了;
#include<iostream> using namespace std; int solve(int x) { int l=0; while (x>0) { l++; z[l] = x%10; x/=10; } memset(f,0,sizeof(f)); memset(g,0,sizeof(g)); f[l+1][1]=1; //边界条件,l+1位往前都是0,是相等的 g[l+1][1]=0; //前L+1位都是0,和也是0 for (int i=l+1;i>=2;i--) //用自己去算别人 for (int j=0;j<=1;j++) //看看是等于还是小于的情况 for (int k=0;k<=9;k++) //枚举这一位我们能填什么 { if (j==1 && k>z[i-1]) continue; //如果前面相同了这一位还大于x的对应位,说明不能填 int j_; if (j==0) j_=0; //如果前面填的数已经小于x了,后面再怎么填都小于x了 else if (k==z[i-1]) j_=1; //如果前面的数等于x,并且这一位还是等于x的对应位,那么新的数还是和x相同 else j_=0; //否则的话就小于x f[i-1][j_] += f[i][j];//加法技术原理求方案数 g[i-1][j_] += f[i][j] * k + g[i][j]; //这一位填上个k,对于每一种方案都可以填上k啊,那么总的贡献就是方案数乘k,别忘了加上之前位数的位数之和 } return g[1][0] + g[1][1]; //答案 } int main() { cin >> l >> r; cout << solve(r) - solve(l-1) << endl; return 0; }

多一个条件多加一个维度。
状态设置:f [ i ][ j ][ k ] 代表前 i 位已经填好了,j = 0 代表小于,j = 1 代表等于,第 i 位填的是 k;
这样的话我们就避开差小于 2 的情况;

状态设置:f [ i ][ j ][ r ] 从高向低填到第 i 为,j判断是否相等,我们已经填的数的数位之积是r;
发现 r 的范围很大,空间爆内存啊,怎么办?
因为 r 是各位数相乘的结果,所以 r 的因子里不可能有超过10的质因子;
也就是说,r 里面的质因子只有2,3,5,7,再根据唯一分解定理,那么 r 一定可以表示为2a * 3b * 5c * 7d ;
多加几个维度:f [ i ][ j ][ a ][ b ][ c ][ d ] 表示从高位往低位填,我们填的数的数位之积是2a * 3b * 5c * 7d;
还可以优化:我们发现 a,b,c,d 不可能同时达到上界,所以我们可以预先处理出 long long 范围内所有满足2a * 3b * 5c * 7d 的数,大约有3W多个,然后改一下状态:f [ i ][ j ][ k ] 表示第 k 个这样的数,这样就不会有任何的空间浪费。
6.树形动态规划
就是在树上做的DP,注意这棵树一定是有根树,否则不能DP;
例题:
给你个 n 个点的树,问你树上有多少个点?
n 个啊(大雾
不,我们要用树形DP!
在每个点,我们维护以它为根的信息;
状态设置:f [ i ] 表示以 i 为根的子树有多少个点;
状态转移方程:f [ i ] = Σ( j ∈son [ i ] ) f [ j ] + 1;
树形DP就是把它所有儿子对应的所有信息转和得到自己的信息;

树的直径:在树上找到两个点,使得这两个点的距离最远;
树的路径大概长这样:
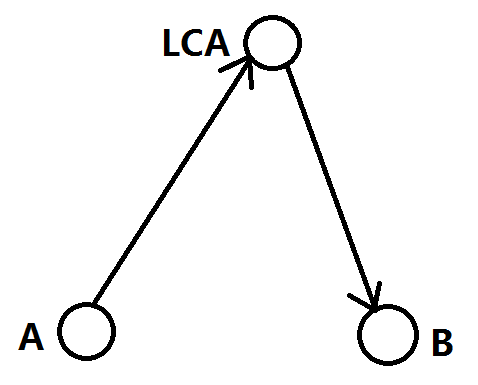
我们发现这个路径就是先向上走到 LCA,再从 LCA 往下走走到另外一个结点;那么我们可以换种角度来看,不就是从 LCA 往下走跳最长路和次长路之和嘛?
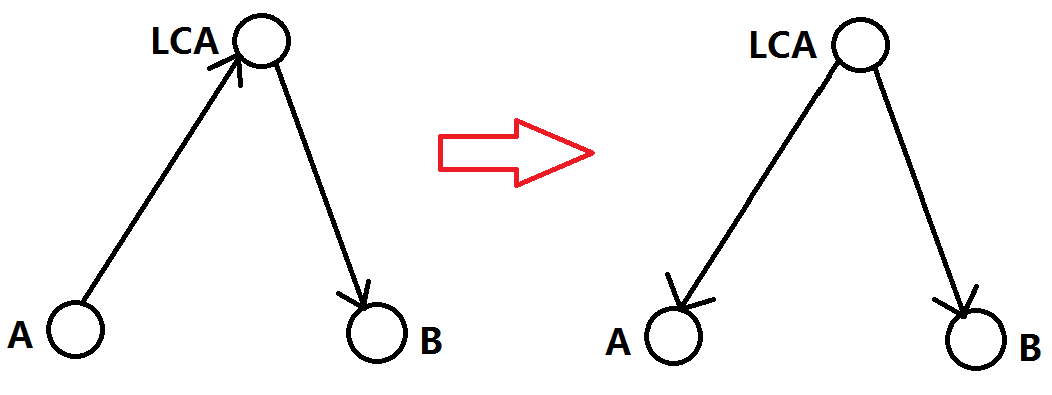
所以我们的问题就转化成:我们求每个点往下走的最长路和次长路。
状态设置:f [ i ][ 0 ] 代表从第 i 个点向下走最长能走多少,f [ i ][ 1 ] 代表从第 i 个点向下走次长能走多少。
答案:求出每个点的 f [ i ][ 0 ] + f [ i ][ 1 ] ,取最大值。
注意到在算第 i 个点的值得时候,下面的点已经被算过了。
f [ i ][ 0 ] = max (f [ Pj ][ 0 ] )+ 1,Pj 表示是 i 的第 j 个儿子;
选 f [ i ][ 1 ] 的时候,一定要避免与 f [ i ][ 0 ] 选到一个结点上去;
所以我们只需要从每个儿子中找到一条最长的,看看是否能更新就好了;
如果有一个儿子的最长路是大于父亲结点的最长路的,那么父亲结点现在的次长路更新为原先的最长路,最长路更新为儿子的最长路+1;否则如果儿子的最长路只大于父亲的次长路,那就更新父亲的次长路;
void dfs(int i) { for (int j=head[i];j;j=e[j].next) { int p=e[j].to; dfs(p); } for (int j=head[i];j;j=e[j].next) { int p=e[j].to; int v = f[p][0]+1; if (v>f[i][0]) //如果大于父亲的最长路 { f[i][1]=f[i][0]; //现在的次长路是原先的最长路 f[i][0]=v; //最长路更新为儿子的最长路+1 } else if (v>f[i][1]) f[i][1]=v;//如果不能更新最长路,那看看能否更新次长路 } }

状态设置: f [ i ] 表示以 i 为根的子树有多少个点;
一条边会被多少条路径经过?
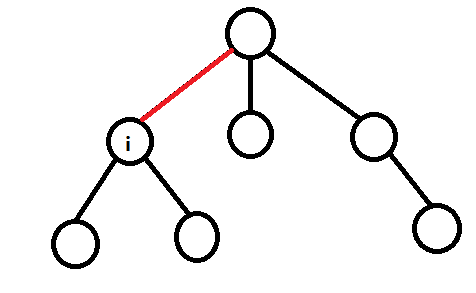
我们要统计红色的这条边对答案的贡献,考虑到这条边的两侧的结点都会经过这一条边,里面(下面)的结点个数是 f [ i ],外面(右边)的结点个数是 n - f [ i ],那么下面的一个点到外面的路径有 n - f [ i ](每个点都要到一遍吧~),那么总共 f [ i ] 个点就有 f [ i ] * (n - f [ i ])跳路径穿过这条边,再考虑外面的点每个点还要到达里面的点一次,所以这条边的贡献就是:2 * f [ i ] * (n - f [ i ]),那么最后的答案就是 Σ(2 * f [ i ] * (n - f [ i ])),i 枚举每条边。

状态设置:f [ i ][ 0/1 ] 从以 i 为根的子树从中选出若干的点的最大值是多少,0 代表 i 这个点没选,1 代表 i 选了;
最后答案:max (f [ 1 ][ 0 ] , f [ 1 ][ 1 ]);
既然 i 选了,那么 i 的所有儿子都不能选,f [ i ][ 1 ] = Σ f [ j ][ 0 ](j∈son [ i ])+ ai;
如果 i 选了,那么 i 的儿子可以选也可以不选,那么 f [ i ][ 0 ] = Σ max ( f [ j ][ 0 ] , f [ j ][ 1 ] ) (j ∈ son [ i ]);

状态设置:f [ i ][ 0/1 ] 表示第 i 个士兵选还是不选;
如果第 i 个士兵不选,那么与儿子相连的边必须要儿子来看着,那么每个儿子都要选:
f [ i ][ 0 ] = Σ f [ j ][ 1 ](j∈son [ i ]);
如果第 i 个士兵选上了,那么儿子们可选可不选,取最小值;
f [ i ][ 1 ] = Σ min(f [ j ][ 0 ] , f [ j ][ 1 ])(j ∈ son [ i ])+ 1;
拓展:
如果每个士兵只能守护与其距离不超过二的边呢?
状态设置:f [ i ][ 0/1/2 ] 以 i 为根的这个子树已经用士兵覆盖住了,i 这个结点向下走到达的最近的士兵的距离是 0/1/2;
0:就是这个结点有士兵;
1:儿子结点有士兵;
2:孙子结点有士兵,儿子结点没有士兵;
f [ i ][ 0 ] = Σ min ( f [ j ][ 0/1/2 ] ) (j ∈ son [ i ])+ 1;
f [ i ][ 1 ] = 由于太danteng,需要再来个DP求!!!
g [ j ][ 0/1 ] 我们已经确定了前 j 个儿子的取值,其中这个这 j 个儿子中有没有一个儿子拿出一个 0 来作为答案(距离最近的士兵的距离是0)
f [ i ][ 2 ] 也要用类似的DP来求!!!
DP套DP可还行;


