7月清北学堂培训 Day 4
今天是丁明朔老师的讲授~
图论
图是种抽象结构,这种抽象结构可以表示点与点之间的关系。
最短路:
Dijkstra(堆优化)
SPFA
Floyd
最小生成树:
Kruscal
连通性:
BFS / DFS
Tarian(强连通分量)
其他:
拓扑排序
LCA
啥都不说先看下经典例题:

30pts:
我们枚举两个点,搜索它的所有路径,如果所有路径的比值(将路径上所有的传动比相乘)一样的话那就OK,否则就无解;
更好的做法:
图的一个良好的性质:
图的 dfs 树只有返祖边,没有横叉边,如果有横叉边的话,dfs 树的形态就会发生改变;
每个点只到达过一次,且是由其他点到达的,这就符合一棵树的性质;
我们不妨先给所有的齿轮顶一个规矩,让这些作为最初的传动比,我们可以枚举一个点所有的非树边,树边作为一组基础的传动比,非树边来判定传动比是否满足就好了。
绪论LCA

Tarian 的 LCA 的时间复杂度:O(n+m);
最短路
单源最短路算法:
Dijkstra:只能处理正边,时间复杂度稳定;

SPFA:可以处理负边,可以判负环,但是时间复杂度很容易被卡;
这里是手写循环队列,STL里的队列也很快,但是不好查 bug;
这里是最长路代码:

多源最短路:
Floyd:
枚举所有中间结点进行扩展;

最小生成树
图的最小的一颗生成树,叫做最小生成树。
图的最小生成树不一定唯一,有个最重要的性质:最大边权最小。
Kruscal
处理无向图的最小生成树。
我们将图的所有边权排一个序,每次取边权最小的一条边,将边的两个端点连到同一个连通块里。
注意到如果两个端点已经在同一个连通块里了,那么我们再连的话就不是最小生成树了,所以我们就舍弃这条边。那么我们问题就转化为如何判断两个点在一个集合中,怎么合并两个点?考虑用并查集!

拓扑排序
拓扑排序可以判环:我们拓扑排序后发现序列的大小不为 n,说明有环;
每次拿掉一个入度为0的点,将这个点的所有出边全部删掉,这样的话就会产生一大批新的入度为0的点,那么我们将其入栈就好了,直到栈里元素为空。

例题:

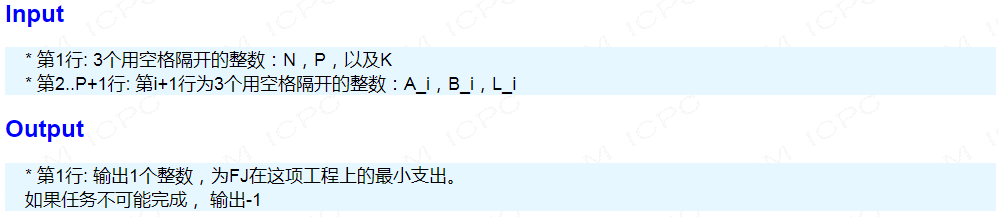
最先题目让求最大值最小,那么用二分;这样本来一个复杂度最大值最小的问题,被我们转化成了简单的判定问题;
我们二分在电话费上花费 mid 元,看是否能从点 1 走到点 n;
接下来我们判定 mid 可行不可行:看能否有小于 k 条边权大于 mid 的边。
我们将全部边权小于 mid 的边的权值设为 0,大于 mid 的边的设为 1,我们跑一遍最短路,得出的答案一定是最小的有大于 mid 的边的条数,如果这个数是小于等于 k 的话(全部将其免费),那就说明这个方案可行,然后我们不断二分直到找到最优解就好了。

直接 Kruscal 就好了,因为最小生成树满足一个性质:最大边权最小,所以如果我们有一个集合内的点的个数等于 n-1 的话,新加进来的那条边就是答案;

我们可以考虑在建图方面进行改造:
假设我们建完图之后是长这个样子的:
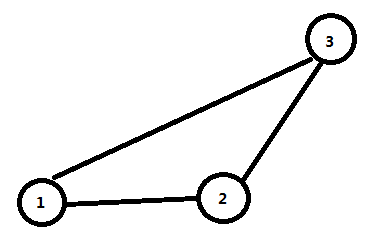
我们先考虑 k=1 的情况,也就是我们可以使一条边的权值变为0.。
我们可以将这个图在上层拷贝一份,将每个结点从上层的能到达的结点连一条有向边,这些边的权值为0,这样就实现了删除一条边的效果:
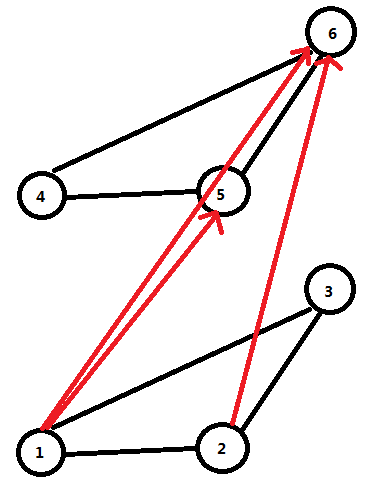
那么怎么设置上层点的编号呢?
我们可以像棋盘一样设置:
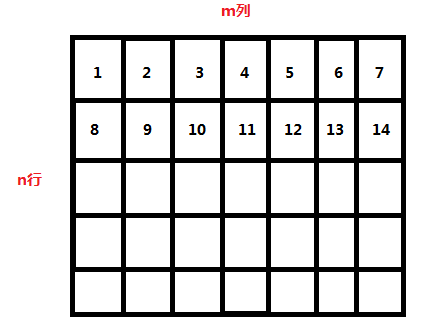
假设我们有个 n × m 的棋盘,那么这个棋盘上第 k 行第 j 列的数就是:(k-1)* m + j;
那么我们也可以根据这个规律来给上层的图的结点编号:(2-1)* n + j;
那么最终的答案就是:1 -> 6 的最短路,一遍Dijkstra 即可;
分析完上面 k=1 的情况后,我们就可以得出删除 k 条边的做法了:
我们拷贝 k 层图,按照上面的思路连权值为0的有向边,那么最后的答案就是:1 -> (k-1)* n 点的最短路;
我们这样建边实现边的跳跃。
分层图的实现:通过映射,将二维图转化为一维图;

翻译一下题面:
虫洞是单向负边,小路是双向正边,我们看是否能回到过去。
其实就是求图中是否有负环。
我们可用SPFA来判定负环:如果一个结点进入队列的次数超过了 n 次,那就说明图中存在负环;
AC代码:
#include<iostream> #include<cstdio> #include<cstring> #include<queue> using namespace std; const int N=200086; const int inf=1e9; int t,m,n,x,y,w,k,edge_sum; int head[N],vis[N],times[N],dis[N]; struct pos { int from,to,next,dis; }a[N]; queue<int> q; void add(int from,int to,int dis) //链式前向星存图 { edge_sum++; a[edge_sum].next=head[from]; a[edge_sum].from=from; a[edge_sum].to=to; a[edge_sum].dis=dis; head[from]=edge_sum; } int spfa() { for(int i=1;i<=n;i++) { vis[i]=0; //有没有在队列里 dis[i]=inf; //初始化无穷大 times[i]=0; //记录每个点入队次数 } vis[1]=1; //题目要求从标号为1的点开始找负环 dis[1]=0; times[1]++; q.push(1); while(!q.empty()) { int u=q.front(); q.pop(); vis[u]=0; for(int i=head[u];i;i=a[i].next) //枚举u的每条出边 { int v=a[i].to; if(dis[v]>dis[u]+a[i].dis) //松弛操作 { dis[v]=dis[u]+a[i].dis; if(!vis[v]) { q.push(v); vis[v]=1; times[v]++; if(times[v]>=n) return 0; //这个是判负环的条件 } } } } return 1; } inline int read() { int a=0,f=1; char ch=getchar(); while(ch>'9'||ch<'0') { if(ch=='-') f=-f; ch=getchar(); } while(ch<='9'&&ch>='0') a=a*10+ch-'0',ch=getchar(); return a*f; } int main() { t=read(); for(int i=1;i<=t;i++) //t组数据 { n=read(); m=read(); k=read(); edge_sum=0; memset(a,0,sizeof(a)); memset(head,0,sizeof(head)); for(int j=1;j<=m;j++) { x=read(); y=read(); w=read(); add(x,y,w); add(y,x,w); } for(int j=1;j<=k;j++) { x=read(); y=read(); w=read(); add(x,y,-w); } if(spfa()==0) printf("YES\n"); //看有没有负环 else printf("NO\n"); } return 0; }

连边技巧:
我们注意到一个街区里的任意两点之间的距离是相同的,所以我们两两连一条边,每条边的边权相同?这样的话我们一个集合要连 n2 条边,显然不行。
假设我们有个集合:
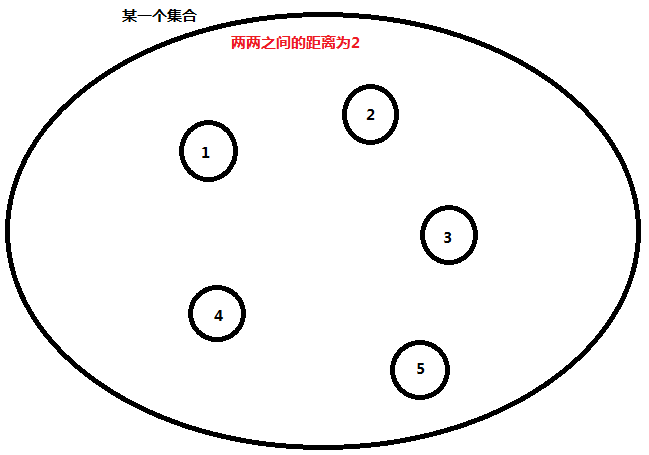
我们可以在每个集合中设一个虚点,使得集合中的每个点到这个虚点的距离为 ti(集合内任意两点的距离):
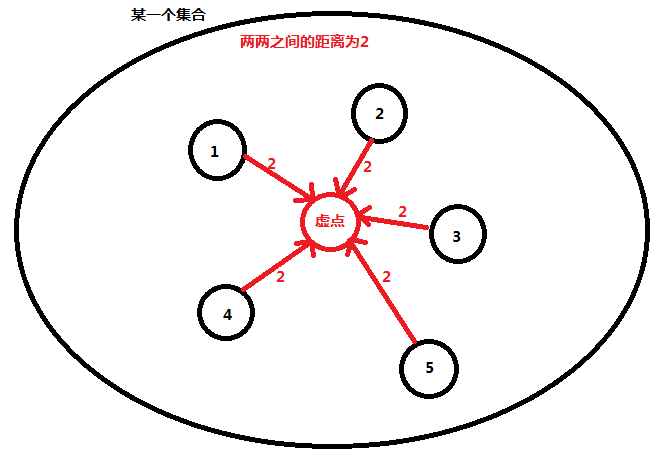
然后我们让这个虚点到每个结点的距离为0:
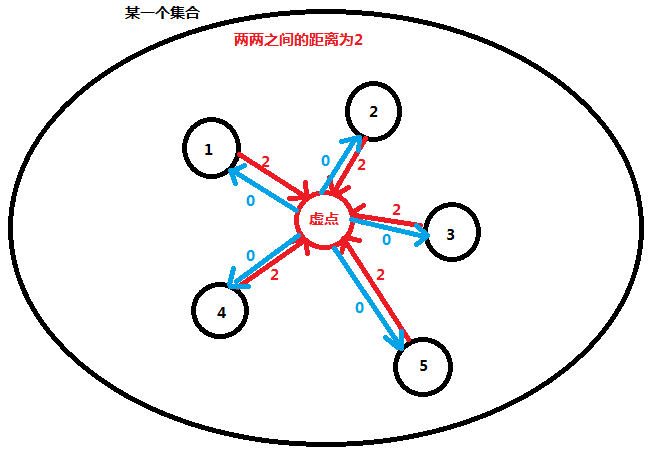
这样建边的话,一个集合只需要建 2n 条边,而能满足集合内任意两点的距离是相等的。(因为都要经过虚点)
我们让每个集合都进行这样的操作后,然后直接 Dijkstra 从 1 -> n 跑一遍最短路即可。

我们最好一开始就在有宝物的位置,这样就不用再动身前往第一个藏有宝物的位置;
我们按照 dfs 序走是最好的,不按 dfs 序走的话可能会走大量的重边;
我们将有宝物的结点按照 dfs 序排序(从小到大),相邻两两求个 LCA,目的是求这两个点的最短路,别忘了求第一个点和最后一个点的最短路(最后还要回去);
那么这个问题我们就已经解决了一半了。
看到题目中宝物是在变换的,那么问题就转化成:在一个序列中(dfs 序),我们每次插入或删除一个数,我们求它的前驱和后继,算一遍最短路,更新答案。
至于求前驱和后继的方法:set,线段树,平衡树;

我们发现Bi,j 范围有些大,其实 300 就够了。
飞飞侠,飞飞侠,我们可以将飞飞侠的每次弹射都看作是依次飞天再降落的过程(方便建图)。
例如,我们花费 A [ i ][ j ] 的费用弹射到 B [ i ][ j ] 的位置可以看成是这样的:
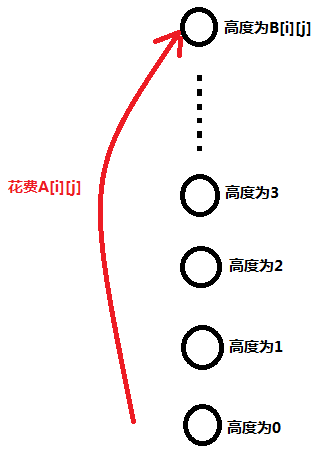
考虑到我们要降落啊,直接往下连一条权值为0的点就行了(下落不需要费用):
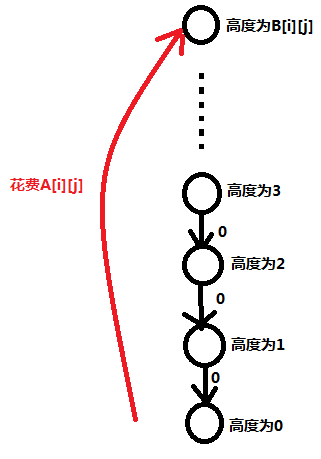
然后我们原地起飞飞了 B [ i ][ j ],但是要移动啊!!!
怎么让它移动呢?
我们将每个点向它的右下方点点连一条权值为 0 的边:
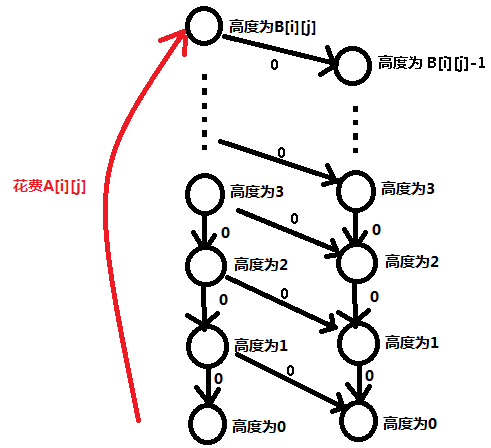
这样的话我们就下降了一个高度移动了 1 个单位的距离。
我们再向右下方连边:
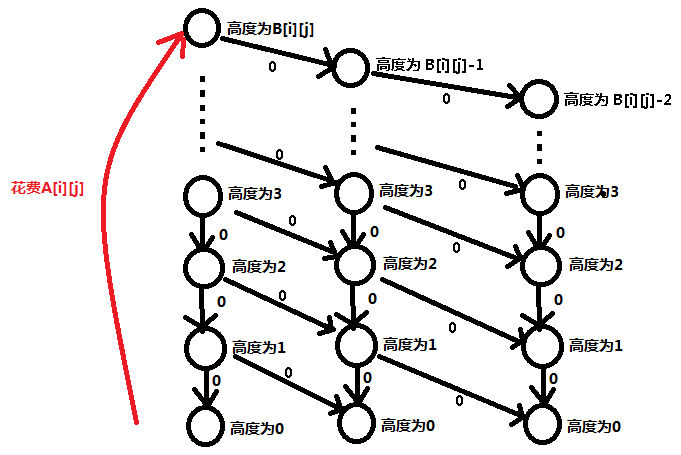
所以我们又下降了一个高度移动了一个单位的距离;
这样做下去我们最多能移动 B [ i ][ j ] 个单位的距离,也就符合了题目的要求。
然后我们跑三遍最短路(三个人),就好了。

图论全是脑子题QwQ~
强连通分量
被定义在有向图当中。
如果两个点能互相到达,就成这两个点是强连通的;
有一个图,任意两个点之间都是强连通的,那么称其为强连通图;
如果图的一个子图是强连通的,就成这个子图是强连通子图;
一个图的极大强连通子图被称为强连通分量;
如果一个图有强连通分量,那么说明这个图中有环;
为了证明强连通分量很重要,先看一道题目:

考虑到一个强连通分量里的所有牛都是受欢迎的,所以我们不妨将所有的强连通分量看作是一个点(缩点)。
如果我们将图中的所有强连通分量都看成一个点的话,那么这个图中一定没有环了;
考虑这样几种情况:
1. 如果我们发现只有一个出度为 0 的点,那么那个出度为 0 的点代表的强连通分量的大小就是答案;
2. 如果我们发现有大于 1 个出度为 0 的点,那么说明至少有两头牛互相不服,那么这时候就没有最受欢迎的牛了。
如何求强连通分量?这就要用到了一个算法:Tarjan。
不妨先求个 dfs 树。
(小知识:无向无环图只有返祖边没有横叉边,而有向无环图可以有横叉边。
dfn [ x ]:表示 x 是第几个被 dfs 到的数;
low [ x ]:当前结点以及它的子树的所有出边的所能连到的 dfn 值最小的那个;
scc [ x ]:表示 x 在第几个强连通分量中;
我们使用tarjan的方法 :
(1)、首先初始化 dfn [ u ] = low [ u ] = 第几个被dfsdfs到
(2)、将 u 存入栈中,并将 vis [ u ] 设为 true
(3)、遍历 u 的每一个能到的点,如果这个点 dfn 为0,即仍未访问过,那么就对点 v 进行 dfs,然后 low [ u ] = min(low [ u ] , low [ v ])
(4)、假设我们已经 dfs 完了 u 的所有的子树,那么之后无论我们再怎么 dfs,u点的 low 值已经不会再变了。
至此,tarjan 完美结束。
那么如果 dfn [ u ] = low [ u ] 这说明了什么呢?
再结合一下 dfn 和 low 的定义来看看吧:
dfn 表示 u 点被 dfs 到的时间,low 表示 u 和 u 所有的子树所能到达的点中 dfn 最小的。
这说明了 u 点及 u 点之下的所有子节点没有边是指向 u 的祖先的了,即我们之前说的 u 点与它的子孙节点构成了一个最大的强连通图即强连通分量;
此时我们得到了一个强连通分量,把所有的 u 点以后压入栈中的点和 u 点一并弹出,将它们的 vis 置为 false,如有需要也可以给它们打上相同标记(同一个数字);
void tarjan(int u){ dfn[u]=++ind; low[u]=dfn[u]; //初始化 s[top++]=u; //这个结点入栈 in[u]=1; //在栈里 for(int i=head[u];i;i=e[i].next){ //枚举u的所有出边 int v=e[i].to; if(dfn[v]==0){ //没遍历到,说明v在子树里面 tarjan(v); //搜v low[u]=min(low[u],low[v]); //更新一下u的值 }else{ //如果之前遍历到过了,说明v不在子树里 if(in[v]){ //如果v在栈里面,说明v比u先遍历到,所以该边是返祖边 low[u]=min(low[u],dfn[v]);//注意这里是dfn[v],因为返祖边 } } } if(dfn[u]==low[u]){ //发现了一个强连通分量 cnt_scc++; //强连通分量的个数加一 while(s[top]!=u){ //将u之上的数都弹出作为这个强连通分量里的元素 top--; in[s[top]]=0; scc[s[top]]=cnt_scc; } } }
例一:

按照 g 升序排序,然后我们从小到大枚举 g0,将所有 g 小于等于 g0 的边拿出来按照 s 求一个最小生成树;
当 g0 逐渐增大时,我们每次比上一次多插入一条边,然后每次往里加边的时候如果形成一个环,那么我们删掉这个环中权值最大的,这样就能维护最小生成树;
发现前面没有用到的边后面也不会再用了,时间复杂度O(n × m);
例二:

一个定理:平面图的最小割等于其对偶图的最短路。
割:使得起点和终点不连通所删去的边所组成的集合;
最小割:所有的割当中边权总和最小的那个割;
怎么画对偶图?
我们将图中的每个三角形抽象看成一个点(红点):
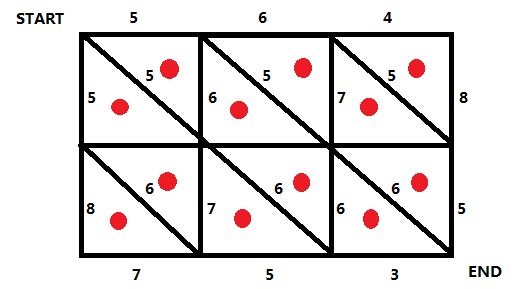
然后我们在左下角和右上角各设置一个点,我们将与这两个点相邻的边上的所有红点连起来,这个边的权值就是连接红点时穿过的边的权值(红点之间也要玄学得连起来,但是注意要对偶):

我们画出来对偶图之后,这个题就基本解决了,我们自己手动走一遍就可以知道:在对偶图中我们从我们设的这个左下角的点走到右上角的点的任意一条路径,删去路径上所有经过的边,都是一个割!而这条路径上每条边的和就是这个割的值;
那么我们的问题就转化成:在这个对偶图上跑一遍最短路就好了,求出的就是最小割。
例三:

求一个环(最后还要回到起点):这个环的点权之和除以边权之和最大;
我们可以把点权转化成边权上,每个边维护两个信息:Ti,Fi;
我们二分枚举一个 t 作为最终答案,那么∑ Ti / ∑Fi <= t,∑ Ti <= ∑Fi * t,∑ Ti - ∑Fi * t <= 0,∑(Ti - Fi * t) <=0;
所以问题就是转化成:判断图中是否有负环。
这种问题被称为分数规划,做法是二分答案+SPFA判负环。
最优比率生成树
求一个生成树 T ,使得 ∑ Ti / ∑Fi 最大。
解法——0/1分数优化:
我们二分答案 t,那么∑ Ti / ∑Fi <= t,∑ Ti <= ∑Fi * t,∑ Ti - ∑Fi * t <= 0,∑(Ti - Fi * t) <=0;
那么问题就转化成:判断图中是否有负环。
例四:

显然强连通分量里的钱我们是都可以抢光光的,那么我们就可以将这个强连通分量缩成一个点,这个点的值就是强连通分量内的值的总和,我们再跑一遍SPFA就好了,在有酒吧的地方取个 max。
例五:

倍增Floyd
Floyd快速幂
g1 [ i ][ j ]:表示从 i 到 j 只经过一条边的最短路;
怎么转移呢?
我们枚举所有中点 k,g2 [ i ][ j ] = min(g2[ i ][ j ] , g1 [ i ][ k ] + g1 [ k ][ j ]);
g4 [ i ][ j ] = g2 [ i ][ k ] + g2 [ k ][ j ];
gn [ i ][ j ] = gn/2 [ i ][ k ] + gn/2 [ k ][ j ];
那么我们怎么求 g19 [ i ][ j ] ?
g3 [ i ][ j ] = g2 [ i ][ k ] + g1 [ k ][ j ];
g19 [ i ][ j ] = min (g16 [ i ][ k ] , g3 [ k ][ j ]);
while(b){ if(b&1){ memset(f,0x3f,sizeof(f)); for(int k=1;k<=n;k++){ for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++){ f[i][j]=min(f[i][j],ret[i][k]+g[k][j]); } } } memcpy(ret,f,sizeof(f)); } memset(f,0x3f,sizeof(f)); for(int k=1;k<=n;k++){ for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++){ f[i][j]=min(f[i][j],g[i][k]+g[k][j]); } } } memcpy(g,f,sizeof(f)); } print(ret[S][E])
例六:

1. 如果两条路径不交叉:
除了最短路上的点,其他全部删掉;
m - dis [ s1,t1 ]- dis [s2,t2 ];
2. 如果两条路径交叉:
我们去枚举两条路径重合的部分,设这段重合的部分就是(i,j)吧,那么我们就将剩余部分全部删去:
假如我们有棵树,且确定好了(s1,t1),(s2,t2):
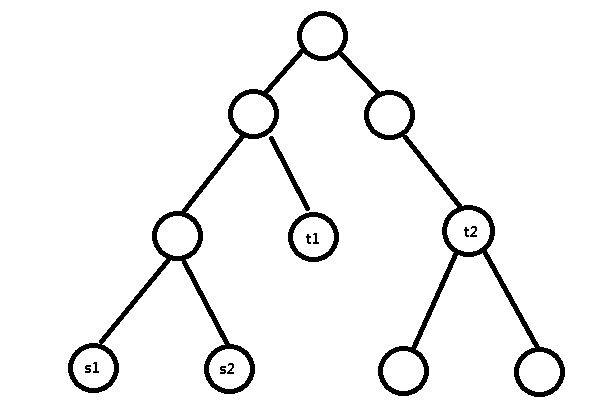
不难看出 s1 --> t1 和 s2 --> t2 的路径:
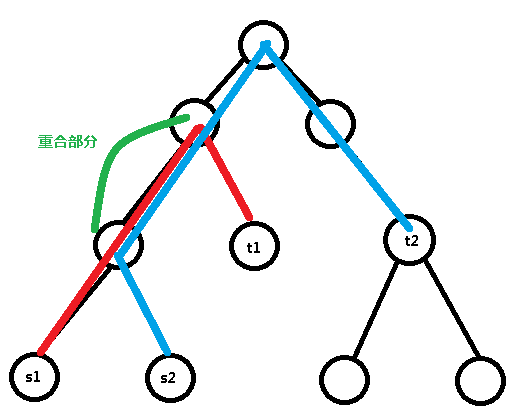
看到两条路径当中有重合的部分,我们就去枚举这个重合部分中的两个中间点 i,j:
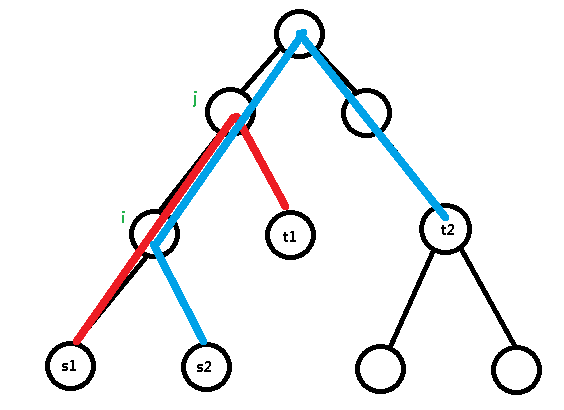
然后我们删掉这两条路径取并集后剩下的所有线段,但是怎么删呢?我们可以将其分成五段:
不同的颜色代表不同的段:
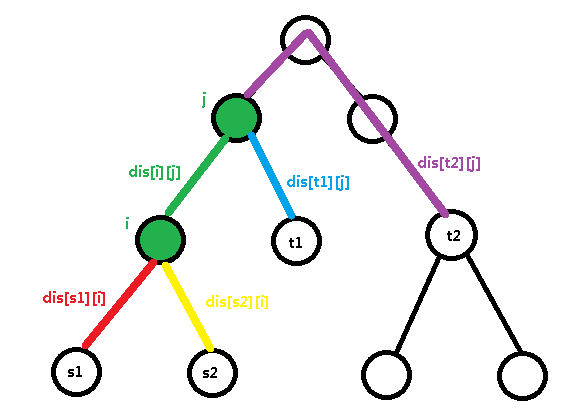
m - dis [ s1 ][ i ] - dis [ j ] [ t1 ] - dis [ s2 ][ i ] - dis [ j ][ t2 ] - dis [ i ][ j ];
这五段就包含了两条路径取并集的所有边,而且这五段也非常好表示。
最后我们可以用 bfs 求最短路。
匈牙利算法
什么是二分图?
二分图又称作二部图,是图论中的一种特殊模型。
设G=(V, E)是一个无向图。如果顶点集V可分割为两个互不相交的子集X和Y,并且图中每条边连接的两个顶点一个在X中,另一个在Y中,则称图G为二分图。
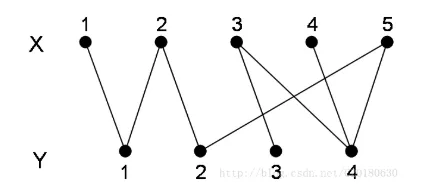
交替路:从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边...形成的路径叫交替路。
增广路:从一个未匹配点出发,走交替路,如果途径另一个未匹配点(出发的点不算),则这条交替路称为增广路。
匈牙利算法的宗旨就是找到一个增广路,实现二分图的最大匹配。
算法轮廓:
1.置 M 为空;
2.找出一条增广路径 P,通过取反操作获得更大的匹配 M’ 代替 M;
3.重复2操作直到找不出增广路径为止;
到这里大家可能也不太明白,那我们先用直白的话来解释一遍:
说穿了,就是你从二分图中找出一条路径来,让路径的起点和终点都是还没有匹配过的点,并且路径经过的连线是一条没被匹配、一条已经匹配过,再下一条又没匹配这样交替地出现。找到这样的路径后,显然路径里没被匹配的连线比已经匹配了的连线多一条,于是修改匹配图,把路径里所有匹配过的连线去掉匹配关系,把没有匹配的连线变成匹配的,这样匹配数就比原来多1个。不断执行上述操作,直到找不到这样的路径为止。
先安利一下图片的原链接 【传送门】
-------等等,看得头大?那么请看下面的版本:
通过数代人的努力,你终于赶上了剩男剩女的大潮,假设你是一位光荣的新世纪媒人,在你的手上有N个剩男,M个剩女,每个人都可能对多名异性有好感(-_-||暂时不考虑特殊的性取向),如果一对男女互有好感,那么你就可以把这一对撮合在一起,现在让我们无视掉所有的单相思(好忧伤的感觉
),你拥有的大概就是下面这样一张关系图,每一条连线都表示互有好感。
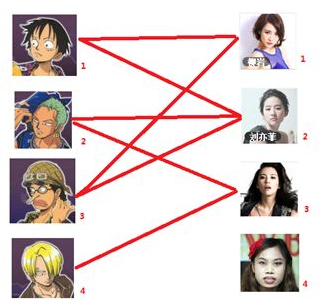
本着救人一命,胜造七级浮屠的原则,你想要尽可能地撮合更多的情侣,匈牙利算法的工作模式会教你这样做:
===============================================================
一: 先试着给1号男生找妹子,发现第一个和他相连的1号女生还名花无主,got it,连上一条蓝线
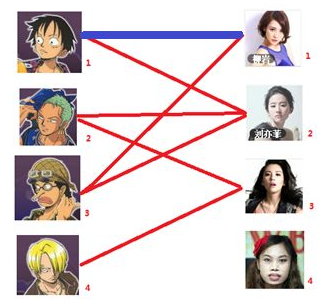
====================================================================
二:接着给2号男生找妹子,发现第一个和他相连的2号女生名花无主,got it
====================================================================
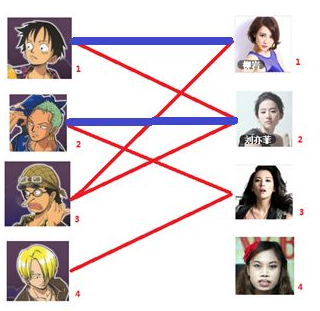
三:接下来是3号男生,很遗憾1号女生已经有主了,怎么办呢?
我们试着给之前1号女生匹配的男生(也就是1号男生)另外分配一个妹子。
(黄色表示这条边被临时拆掉)
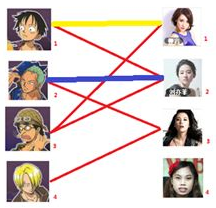
与1号男生相连的第二个女生是2号女生,但是2号女生也有主了,怎么办呢?我们再试着给2号女生的原配()重新找个妹子(注意这个步骤和上面是一样的,这是一个递归的过程)
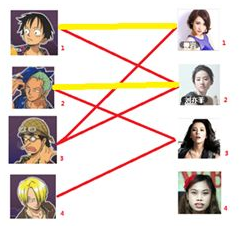
此时发现2号男生还能找到3号女生,那么之前的问题迎刃而解了,回溯回去
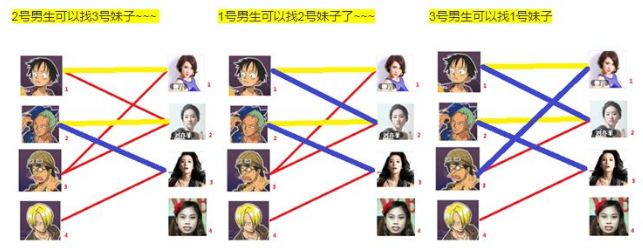
所以第三步最后的结果就是:
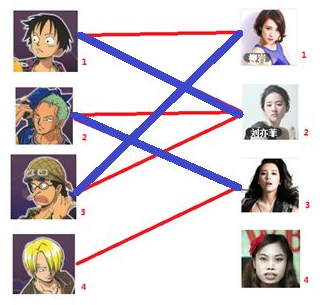
===============================================================
四: 接下来是4号男生,很遗憾,按照第三步的节奏我们没法给4号男生腾出来一个妹子,我们实在是无能为力了……香吉士同学走好。
===============================================================
这就是匈牙利算法的流程,其中找妹子是个递归的过程,最最关键的字就是“ 腾 ”字;
其原则大概是:有机会上,没机会创造机会也要上!
代码也很好懂滴:
int vis[10001],girl[10001]; //girl[i]表示第i个妹子喜欢哪个男的,vis[i]表示当前这一轮妹子有没有被考虑过 int f[1001][1001]; //f[i][j]表示i和j是否有好感 bool work(int x) { for(int i=0;i<n;i++) //寻找每个妹子 { if(!vis[i]&&f[x][i]) //如果这个妹子没被别的男的考虑过并且他俩又好感,可以尝试匹配一下 { vis[i]=1; //这个妹子在这一轮我已经考虑过了,其他男的别想了 if(!girl[i]||work(girl[i])) //如果妹子没有喜欢的人或者妹子喜欢的那个人可以找到另一个妹子的话 { girl[i]=x; //那就将这个妹子安排给 x return 1; } } } return 0; //否则的话就安排不上了,没有哪个男的会白白让出自己的妹子的QAQ }

裸的匈牙利算法。
只不过需要注意如果我们当前有一个题没有找到锦囊,那么后面就不用再找了,直接 break 跳出就好了。
差分约束
差分约束系统,是求解关于一组变数的特殊不等式组之方法。
如果一个系统由个变量和
个约束条件组成,其中每个约束条件形如
![]() ,则称其为差分约束系统。亦即,差分约束系统是求解关于一组变量的特殊不等式组的方法。
,则称其为差分约束系统。亦即,差分约束系统是求解关于一组变量的特殊不等式组的方法。
一.树形结合
然后继续回到单个不等式上来,观察 x [ i ] – x [ j ] <= a [ k ] , 将这个不等式稍稍变形,将 x [ j ] 移到不等式右边,则有 x [ i ] <= x [ j ] + a [ k ] ,然后我们令 a [ k ] = w( j, i ),再将不等式中的 i 和 j 变量替换掉,i = v, j = u,将 x 数组的名字改成 d(以上都是等价变换,不会改变原有不等式的性质),则原先的不等式变成了以下形式:d [ u ] + w( u, v ) >= d [ v ]。
这时候联想到SPFA中的一个松弛操作:
if(d[u] + w(u, v) < d[v])
{ d[v] = d[u] + w(u, v); }
对比上面的不等式,两个不等式的不等号正好相反,但是再仔细一想,其实它们的逻辑是一致的,因为SPFA的松弛操作是在满足小于的情况下进行松弛,力求达到 d [ u ] + w( u, v ) >= d [ v ],而我们之前令 a [ k ] = w( j, i ),所以我们可以将每个不等式转化成图上的有向边:对于每个不等式 x [ i ] – x [ j ] <= a [ k ],对结点 j 和 i 建立一条 j -> i的有向边,边权为 a [ k ],求 x [ n-1 ] – x [ 0 ] 的最大值就是求 0 到n-1的最短路。
二.三角不等式
如果还没有完全理解,我们可以先来看一个简单的情况,如下三个不等式:
B – A <= c (1)
C – B <= a (2)
C – A <= b (3)
我们想要知道C – A的最大值,通过(1) + (2),可以得到 C – A <= a + c,所以这个问题其实就是求 min { b, a+c }。将上面的三个不等式按照数形结合中提到的方式建图:

发现 b 和 a+c 都是 A -> C 的路径,我们实际上再求最短路!
这就是著名的三角形不等式,将三个不等式推广到m个,变量推广到n个,就变成了n个点m条边的最短路问题了。
三. 最大值 => 最小值
然后,我们将问题进行一个简单的转化,将原先的”<=”变成”>=”,转化后的不等式如下:
B – A >= c (1)
C – B >= a (2)
C – A >= b (3)
然后求C – A的最小值,类比之前的方法,需要求的其实是 max { b, c+a },于是对应的是图三-2-1从A到C的最长路。同样可以推广到n个变量m个不等式的情况。
所以我们求最小值就跑最长路,求最大值就跑最短路!





