7月清北学堂培训 Day 3
今天是丁明朔老师的讲授~
数据结构
绪论
下面是天天见的:
栈,队列;
堆;
并查集;
树状数组;
线段树;
平衡树;
下面是不常见的:
主席树;
树链剖分;
树套树;
下面是清北学堂课程表里的:
ST表;
LCA;
HASH;
堆
支持两种操作:
1.插入一个值;
2.删除一个最大值(大根堆)或最小值(小根堆);
需要使用STL里的 priority_queue 或手写;
LCA
结点 A 和结点 B 的最近公共祖先 LCA 及以上都是 A 和 B 的公共祖先;
注意 LCA 是尽局限于树上的;
如何求两个结点 A 和 B 的 LCA?
1. 如果 A 的深度比 B 的深度小,那么我们将 A 和 B 互换一下,这是为了方便处理;
2. 把 A 向上抬升到 B 的深度;
3. A 和 B 一块往上走,直到走到一个点为止;
如何快速地将 A 和 B 抬升到一个深度?
我们发现 A 和 B 是有深度差的,记为:deep = dA - dB ;
如果我们一步一步地往上跳,要跳 deep 次,我们发现当这个树是一条链的话,时间复杂度会达到O(n),有很大的劣势,我们需要改进一下:
我们可以设计这样一个数组:p [ x ][ i ] 表示 x 的第 2i 个祖先是哪个;
边界条件:p [ x ][ 0 ] = y,y 是 x 的父亲,这个我们用深度优先搜索就可以实现;
一个显然的递推方程:p [ x ][ i ] = p [ p [ x ][ i-1] ][ i-1 ];(x 向上走 2i 就相当于先走 2i-1 再走 2i-1)
我们可以将 deep 用二进制表示出来,为了便于理解这里设 deep=19 吧:
deep = 19 = (10011)2 = 24 + 21 + 20
那么也就是说,我们可以将 A 先往上跳 24 ,再往上跳 21,再往上跳 20 ,也跳到了 B 的深度;
那么我们看到我们定义的数组,不就是 A = p [ A ][ 4 ] => A = p [ A ][ 1 ] => A = p [ A ][ 0 ];我们只跳了三步就OK了。
时间复杂度 O(log n);
如何快速地将 A 和 B 走到同一位置?
我们发现 A 和 B 一旦走到了最近公共祖先 LCA 后,那么以后肯定都在一个位置了,但是我们不好确定这个 LCA 在哪里;
虽然不好确定 LCA 在哪,但是我们可以确定最后一次不相遇的位置:
我们从大到小枚举 i ,让 A 和 B 同时跳 2i ,如果发现跳了之后还是到不了同一个点,那就跳,否则就不跳;
证明的话很简单,因为 dLCA - dA 也可以用二进制表示出来,所以我们是一定能够到达这个 LCA 的,我们按照上述操作后,那么 A 和 B 一定就是 LCA 的左右两个儿子,所以我们再跳一次就是 LCA了;过程中主要如果能跳到同一点就不跳,因为我们不能确定这是不是 LCA;
LCA 常运用处理一类带差分,可差分的问题:
假如我们有棵树:
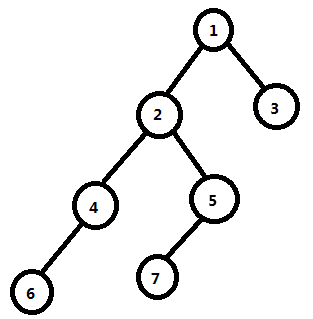
我们要求结点 6 和 7 的最短路径,我们可以先求出 6 和 7 的LCA是 2,然后答案就是deep7 + deep6 - 2 * deep2:
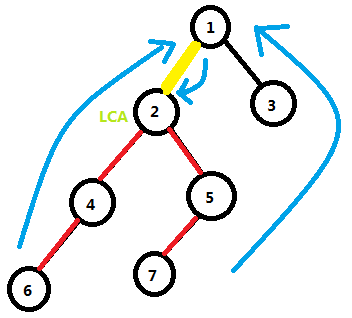
ST表
主要是处理区间最值的 RMQ 问题;
我们设 mx [ i ][ j ] 表示下表从 i ~ i + 2j - 1 内的最值是多少;
边界条件:mx [ i ][ 0 ] = i;
递推方程:mx [ i ][ j ] = max(mx [ i ][ j-1 ] , mx [ i+2j-1 ][ j-1 ]);
mx [ i ][ j ] = min (mx [ i ][ j-1 ] , mx [ i+2j-1 ][ j-1 ]);
这里我们可以将 [ i , i+2j -1 ] 这个长度为 2j 的区间平均分成两个长度为 2j-1 的小区间:[ i , i+2j-1-1 ] 和 [ i+2j-1 , i+2j-1 ],那么大区间的答案不就是两个小区间的答案取最优嘛?这不就完了?
for(int j=1;(1<<j)<=n;j++) for(int i=1;i+(1<<j)-1<=n;i++) f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
在考虑询问的时候,我们要找两段长度相同的区间能覆盖询问区间,我们可以这样做:
先算出询问区间的长度 len = r - l + 1,然后我们取 len 的 log 值向下取整: t = floor(loglen),那么 2t 就能覆盖询问区间的一半,那么我们再来一个就能全部覆盖了。
int l=read(); int r=read(); int k=(int)(log((double)(r-l+1))/log(2.0)); int ans=max(f[l][k],f[r-(1<<k)+1][k]);
哈希HASH
HASH是一种函数,我们需要设计一种函数将一个字符串变成一个数,所以我们在比较两个字符串的时候,就可以比较两个数了;
map 是基于比较函数的红黑树,两个字符串的比较是O(字符串长度),非常非常慢!
我们怎么将一个字符串转化成HASH值?
1.我们先设定这个字符串是个几进制的数(最好取质数);
2.我们可以将原字符串里的字母转化成ASCII 码,然后再将其转化成十进制的数,就是这个字符串的HASH值了。注意到这个数可能很大,所以我们要在后面模一个大质数。考虑到unsigned long long 的范围是 1~ 264- 1,是个质数耶,所以我们可以用unsigned long long 来存让它自然溢出就行了,完全不用管取模的事。
HASH是允许冲突的!我们只是要尽可能避免冲突!而不是根本上消除冲突! 如果我们非常害怕冲突,我们可以双哈希。(将这个字符串用两种进制表示,再模两个不同的质数)

假设我们有一个字符串 dmstql,我们要将它转成HASH值:
1.我们先设定这个字符串是个 p 进制的数;
2.将其转化为十进制(字母换成ASCII码):
HASH = d * p5 + m * p4 + s * p3 + t * p2 + q * p1 + l * p0;
我们怎么求一个字符串子串的HASH?我们求每个字符前缀的HASH,然后可以利用前缀和的思路来求子串的HASH:
d:d * p0;
dm:d * p1 + m * p0;
dms:d * p2 + m * p1 + s * p0;
dmst:d * p3 + m * p2 + s * p1 + t * p0;
dmstq:d * p4 + m * p3 + s * p2 + t * p1 + q * p0;
dmstql:d * p5 + m * p4 + s * p3 + t * p2 + q * p1 + l * p0;
我们发现第 i 个字符前缀哈希值 = 第 i-1 个字符的前缀哈希值 * p + Si(Si 是第 i 个字符)
那么我们怎么求 stq 的哈希值?
手写一下很显然,就是:s * p2 + t * p1 + q * p0,那么怎么用前缀和的形式来表达呢?
其实很很显然了:
HASHdmstq - HASHdm * p3
= (d * p4 + m * p3 + s * p2 + t * p1 + q * p0)- (d * p1 + m * p0)* p3
= (d * p4 + m * p3 + s * p2 + t * p1 + q * p0)- (d * p4 + m * p3)
= s * p2 + t * p1 + q * p0
=HASHstq
至于后面要乘上 p 的几次方这个问题,我们只要看我们求的这个字符串的长度就好了,这里 stq 的长度是 3,所以后面乘上 p3;
并查集
支持合并集合和查找在哪个集合里
定义一个数组:fa [ i ] 表示 i 的父亲是哪个结点,注意树根的父亲是自己;
初始化:fa [ i ] = i,表示每个结点都是独立的;
路径压缩:
我们发现并查集完全没有必要保留树的结构,所以我们直接将一个结点 x 的父亲设为它的祖先;
int getfa(int x) //寻找x的父亲 { fa[x]==x?return x:return getfa(fa[x]); }
树状数组
支持单点修改,区间查询;
主要应用:
线段树常数过大时
线段树功能过多时
树状数组所求的所有问题必须存在逆元!
int lowbit(int x) //求lowbit { return x&(-x); } void modify(int x,int y) //将第x个数加上y { for(int i=x;i<=n;i+=lowbit(i)) c[i]+=y; //加lowbit找父亲 } int query(int x) //询问x的前缀和 { int ret=0; for(int i=x;i;i-=lowbit(i)) ret+=c[i]; return ret; } int query(int l,int r) //区间[l,r]的和 { return query(r)-query(l-1); }
二维树状数组
树状数组的每一个节点都是一个树状数组,所以把循环复制一遍即可。
线段树
支持区间修改,区间查询;
主要应用:
用于处理一类区间修改区间查询的问题。
树的每个结点是一个抽象的线段;
单点修改:
1.定位点的位置;
2.更新树的权值;
任何一段线段在线段树中都以用 log n 条线段表示;
区间修改,区间查询:
要用到懒标记 Lazy Tag,表示这个结点对应的区间的每个数都加上了 x(x存在 Lazy Tag 里);
它的作用是:我们区间加上 x 后,我非常懒不立刻加,不询问到这个结点的话,我就啥也不干,询问到才加上这个 x;
什么时候下传标记?
只要我们要遍历到该结点,就要将它父亲的标记下放;
struct Node{ int l,r; int sum; int tag; }t[N<<2]; void pushup(int rt){ //num上传 t[rt].sum=t[rt<<1].sum+t[rt<<1|1].sum; } void pushdown(int rt){ //标记下传 if(t[rt].tag){ t[rt<<1].tag+=t[rt].tag; t[rt<<1].sum+=t[rt].tag*(t[rt<<1].r-t[rt<<1].l+1); t[rt<<1|1].tag+=t[rt].tag; t[rt<<1|1].sum+=t[rt].tag*(t[rt<<1|1].r-t[rt<<1|1].l+1); t[rt].tag=0; } } void build(int rt,int l,int r){ //建树 t[rt].l=l; t[rt].r=r; if(l==r){ t[rt].sum=a[l]; return; } int mid=(l+r)>>1; build(rt<<1,l,mid); build(rt<<1|1,mid+1,r); pushup(rt); } void modify(int rt,int p,int c){ //单点修改 if(t[rt].l==t[rt].r){ t[rt].sum=c; return; } pushdown(rt); int mid=(t[rt].l+t[rt].r)>>1; if(p<=mid) modify(rt<<1,p,c); else modify(rt<<1|1,p,c); pushup(rt); } int query(int rt,int l,int r){ //询问区间[l,r]的和 if(l<=t[rt].l&&t[rt].r<=r){ return t[rt].sum; } pushdown(rt); int ret=0; int mid=(t[rt].l+t[rt].r)>>1; if(l<=mid) ret+=query(rt<<1,l,r); if(mid<r) ret+=query(rt<<1|1,l,r); return ret; } void add(int rt,int l,int r,int c){ //[l,r]上每个数加上c if(l<=t[rt].l&&t[rt].r<=r){ t[rt].tag+=c; t[rt].sum+=c*(t[rt].r-t[rt].l+1); return; } pushdown(rt); int mid=(t[rt].l+t[rt].r)>>1; if(l<=mid) add(rt<<1,l,r,c); if(mid<r) add(rt<<1|1,l,r,c); pushup(rt); }
总结:
堆:最大值插入,删除,查询;
ST表:区间最大值查询;
树状数组:单点修改,区间查询;
线段树:区间修改,区间查询;
看例题:
例一

我们维护两个堆,一个大根堆,一个小根堆,使得大根堆内的元素个数是 n/2 + 1,小根堆内的元素个数是 n/2,每次插入的时候往大根堆里面插,如果元素个数超过了 n/2 + 1 的话我们就将大根堆的堆顶弹入小根堆里,插完之后大根堆的堆顶就是中位数。(这个的话应该挺好理解的:因为大根堆里面有 n/2 + 1个数,所以比堆顶元素小的有 n/2 个数,比堆顶元素大的都弹到小根堆里面了,也有 n/2 个数,那么这个数不就是中位数嘛?)
例二


我们可以将每个点向右向下连一条边,权值就是这两个点的高度差的绝对值,然后我们将所有的边升序排序,每次取出一条边就将连着的两个端点合并,若发现集合中的点的个数等于T,那么这个集合的贡献就是:最新加入的这条边的权值 * 这个集合中出发点的个数;
做法就是并查集啦~
例四

这个题是树的哈希。
我们看到这个题没有规定树的根,这求起来就有点麻烦啊。不过我们看到数据范围很小,所以我们可以以每个结点为根求一个HASH,如果发现有两个HASH值完全相同,那么就说明这两棵树是同构的。
更巧妙的做法:
一个无根树的中心不会超过两个。
枚举每个重心,以重心为根求出这棵有根树的最小表示,然后取字典序最大的即可。
也可以用括号序来做:
对于有根树的最小表示,可以看成括号序列,每次把子树的括号序列按字典序排序后依次串连起来即可。
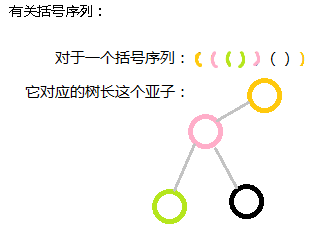
父亲结点的括号括着儿子结点的括号,兄弟结点的括号是并列关系的。
例五:

我们不用归并排序,考虑用树状数组做。
假设我们有个序列 :
1 9 2 6 0 8 1 7
我们只要求出来每个数前面有几个数比它大,就是这个数贡献的逆序对数,我们只要把所有数的逆序对数加起来就好了。
做法:
我们开一个 vis 数组,每输入一个数,将它的 vis 值赋成 1,
问题变成了动态将某个点加一,动态维护前缀和;
离散化:
1.排序 sort;
2.去重 unique;
3.安排查找 lower_bound;
例六:

由于我们要统计一个星星 i 左下角的星星数,那么就是要统计所有的 xj <= xi,yj <= yi,因为我们是按照 y 递增来输入的星星,所以所有比当前星星的 y 值小的星星都已经被输入了,那么我们就考虑之前输入的星星有多少颗星星的 x 值小于等于当前星星的 x 值就好了。
我们开一个数组,S [ i ] 表示横坐标x为 i 的星星个数,那么所有横坐标小于等于 i 的星星个数就是:S [ 1 ] + S [ 2 ] + S [ 3 ] + ……+ S [ i ],求前缀和我们可以用树状数组!
这个题是二维偏序,一维排序,一维树状数组。
例七:

我们开 m 个树状数组。
第 i 个树状数组的第 j 个下标表示 aj % m 是否为 i,是则为1,否则为 0;
加法减法还是正常的加加减减,我们重点考虑询问的情况:
我们询问区间 [ l , r ] 有多少个数模 m ==mod,我们就在第 mod 个树状数组里面找,考虑到一段区间内的和就是这一段区间内模 n == i 的数的个数,所以我们可以利用前缀和思想(树状数组来维护前缀和)分别求出 sum [ r ] 和 sum [ l-1 ] 再做差就可以了。
例八:

对于一个数 x,我们从前找不大于 x 的最大数和从后找不小于 x 的最小数,然后分别与 x 做差取最小的绝对值就是答案;
我们建立一棵线段树维护区间最小值和最大值;(权值线段树:下标不是数组的下标,而是权值的下标)

我们维护两个 Tag,一个记录加法,一个记录乘法,它们之间会互相影响;
考虑到我们在区间乘法的时候,不仅乘法标记要乘上 x,加法标记也要乘上 x;标记下传的时候,考虑到乘法标记优先下传更优,所以将加法标记下传的时候也要乘下乘法标记;

我们发现原数组 a 没有什么卵用啊,我们要求的是斐波那契数求和,所以我们用线段树来维护区间内的斐波那契数的和;对于我们将原数组的某个数加上了 x,其实就是该项的斐波那契数往后推了 x 项,那么我们直接在线段树中将该位置乘上((1 0)(1 1))x 就行了。
这个题告诉我们,线段树懒标记打的不一定是个数,还可能是个矩阵或一些更加奇怪的东西。

发现这个题跟昨天 lyd 讲的分块的题有些类似。
我们开根号的时候,我们看看这个数是否已经被开到了1 或 0,如果是就打上个标记,以后再也不管了(√1=1,√0=0),如果一个结点的左右儿子都被打上标记了,那么我们就将这个结点打上标记;然后就做完了。

满足插入一个数,删除一个数,求中位数之和。
注意到我们插入删除数的时候,中位数可能会改变。
我们开一个 s 数组,s [ i ] 表示下标模5为 i 的数的和;
然后我们就可以线段树每一个结点维护这么一个数组:
假如我们有一个序列:0 1 2 6 7 8 9 11
根结点只有一个元素,所以下标都是 1:

然后得到倒数第二层的数,要将右儿子滚动左儿子数的个数次:
例如:10000 -> 01000
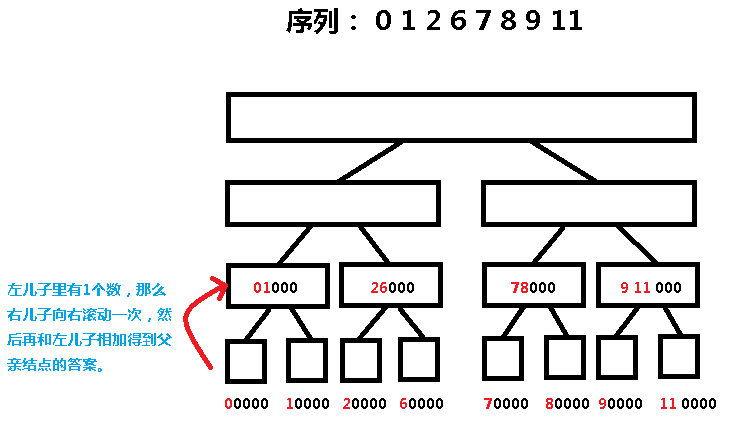
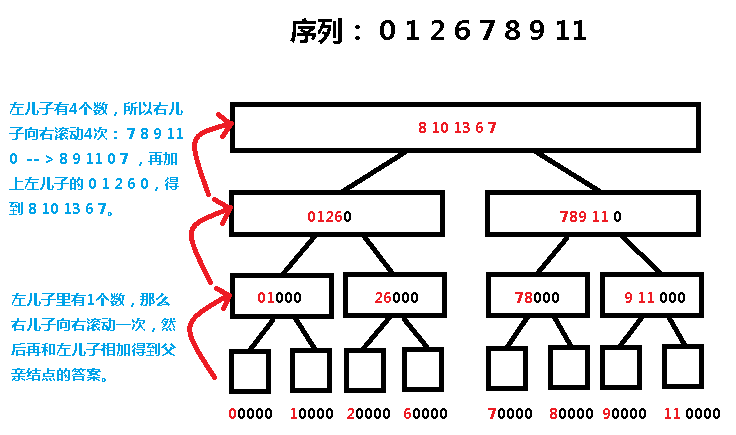
答案就是根结点的 s [ 3 ];
具体做法:
先将要处理的数字离散化。
按数字的顺序为下标建立一颗线段树。
线段树的每个节点维护如下几个值:
这一段闭区间中有几个数字;
s [ 0~4 ]表示下标模5余某的数值之和。
单点修改,区间查询即可完成操作。
告诉我们线段树里维护的不一定是个数,也可能是某种信息,这也是比较常考的。

mex:没出现过的最小的自然数。
我们从左往右扫一遍就可以得到所有以 1 为左端点的区间的 mex 值;
我们每次讲左端点 l 右移一个单位,r 也不断改变,同时更新新区间的 mex 值;
考虑到如果一个数在序列里仅出现过一次,那么如果将这个点删去的话,在这个点右边的那些 mex 比这个数大区间的 mex 值就会被更新成这个数。
单词询问的时间复杂度是O(log n),它的复杂度就是区间修改;
只有查询没有修改:
1.线段树离线;
2.莫队算法;

其实这个题我们只要看有没有长度为 3 的等差序列就好啦。
这个题一个灰常重要的前提:1~n 在序列里全都出现过一次!
我们用一个 vis 数组,将之前出现过的数标记为1,没出现的数标记为0,不妨枚举等差中项 x,我们以 x 为对称轴,看看左右的 vis 是否对称,如果不对称就说明有解,否则的话就说明以 x 作为等差中项是无解的。
单点修改,如何比较两段区间是否相同。
线段树的每一个结点代表的维护这个结点的线段的哈希值,我们要维护两种哈希值,一个往前一个往后。
举个例子:
我们有个序列: 9 3 1 7 5 6 8 2
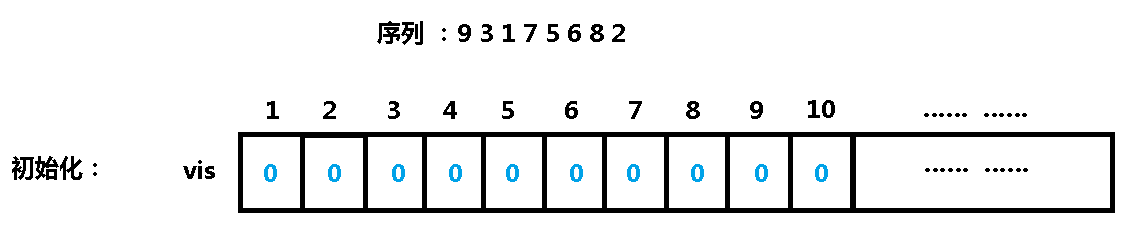
我们先插入9,将 vis [ 9 ] 标记为 1,并看看以 9 为对称轴两边的 vis 值是否对称:
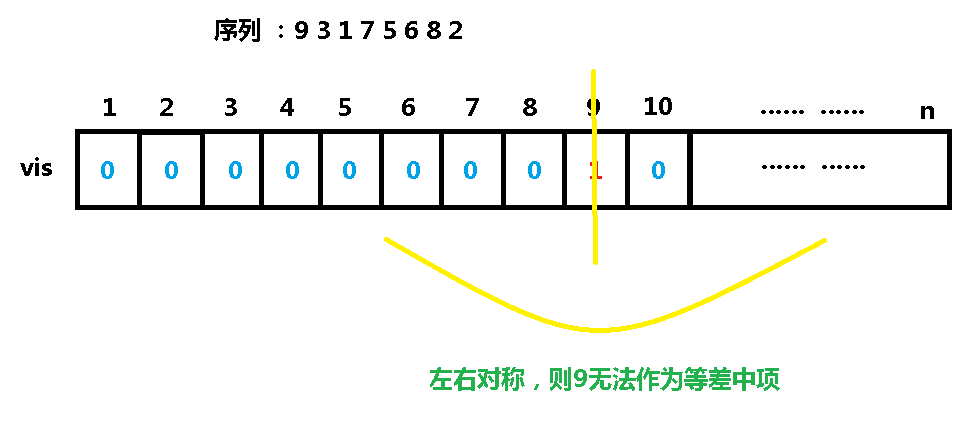
再插入3,将 vis [ 3 ] 标记为 1,并判断以 3 为对称轴左右的 vis 值是否对称:

再插入1:
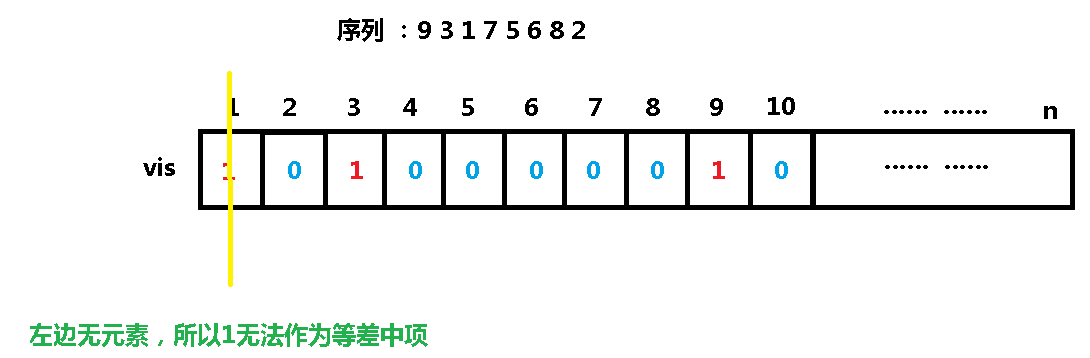
再插入7:

为什么可以介个样做呢?
考虑到当前插入一个数是 x 吧,发现 vis [ x - a ] = 1,说明 x - a 在 x 之前已经出现过了,则 x - a 在 x 的左边;我们又发现 vis [ x + a ] = 0 (x + a <=n),说明 x + a 会在 x 之后出现,这样不就有了一个长度为 3 的等差序列了嘛?这道题就做完了。

平衡树
二叉搜索树的性质:
对于每个结点,它的所有左子树的所有结点都小于这个结点,右子树的所有结点都大于这个结点;
二叉搜索树的查找:
从根结点出发,如果查找元素大于这个结点,就往右子树找,否则就往左子树找;
我们发现二叉搜索树的形态不固定,又因为二叉查找树非常依赖于它的深度,所以用平衡树就能缩短深度;
它支持区间修改,区间查询;
主要实现方式有 Splay、Treap 两种;
平衡树基于一定的操作:旋转(rotate)

旋转之后,我们会发现 1 往上移了一个深度,我们不断旋转不断往上移,直到移到根,这样我们询问是就可以O(1)询问了;
Splay
背景简介:
伸展树(Splay Tree),是一种二叉搜索树,它能在 O(log n)内完成插入、查找和删除操作。
它由丹尼尔·斯立特和罗伯特·恩卓·塔扬在 1985 年发明的。
Splay的特点:
在伸展树上的一般操作都基于伸展操作:假设想要对一个二叉查找树执行一系列的查找操作,为了使整个查找时间更小,被查频率高的那些条目就应当经常处于靠近树根的位置。 于是想到设计一个简单方法, 在每次查找之后对树进行重构,把被查找的条目搬移到离树根近一些的地方。伸展树应运而生。伸展树是一种自调整形式的二叉查找树,它会沿着从某个节点到树根之间的路径,通过一系列的旋转把这个节点搬移到树根去。
cnt [ i ]:当前结点 i 的数出现过多少次;
data [ i ]:当前结点 i 的权值是多少;
size [ i ]:当前结点 i 及其子树里有多少个数;
由于 splay 的旋转操作是整个结构的核心,所以我们先研究下 splay 的旋转操作:
先看一个简单的树,我们将 x 这个结点旋转后应该是这个样子:

怎么知道旋转后是这个样子的呢?
splay 的旋转指的是将当前结点旋转到它的父亲结点上去(保证每次旋转这个点的深度-1),那么图中的 x 结点顺时针旋转后就跑到了 y 结点的位置:
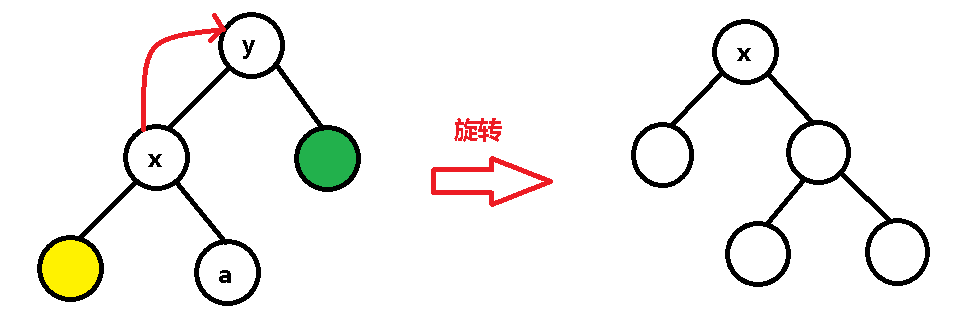
y 结点被赶出来了,只好也顺时针旋转,于是乎跑到了绿点的位置:
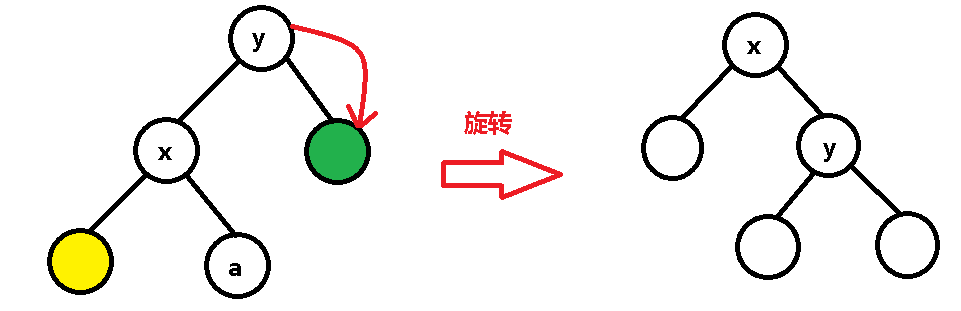
绿点呢?原来它是 y 的右儿子,旋转之后看到 y 的右儿子那里目前还空着,那就接着当 y 的右儿子呗~:

我们看黄点,它之前是 x 结点的左儿子,x 转过去之后发现 x 的左儿子的位置还空着,那就接着当 x 的左儿子呗~:
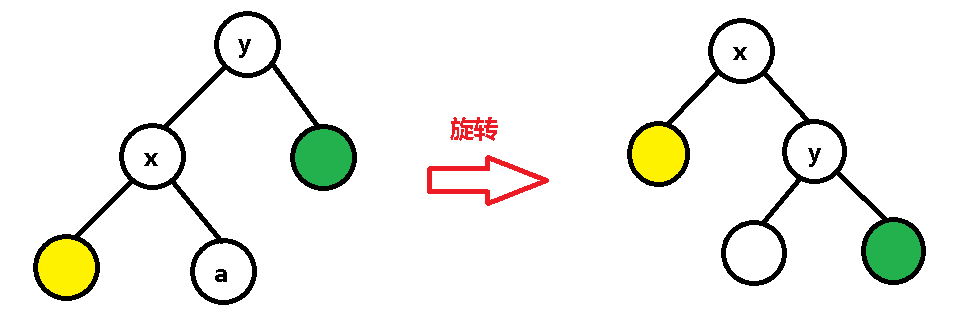
但是 a 就不是很幸运了,x 右儿子的宝座给 y 占了,那怎么办呢?总得给 a 安排个位置吧。
我们就要在维护 BST 的同时给 a 找一个合适的位置 QwQ~
根据 BST 的性质可知,a 是小于 y 的,看到旋转之后 y 没有左儿子哎,那就顺理成章的接到 y 的左儿子那里就好了鸭~:
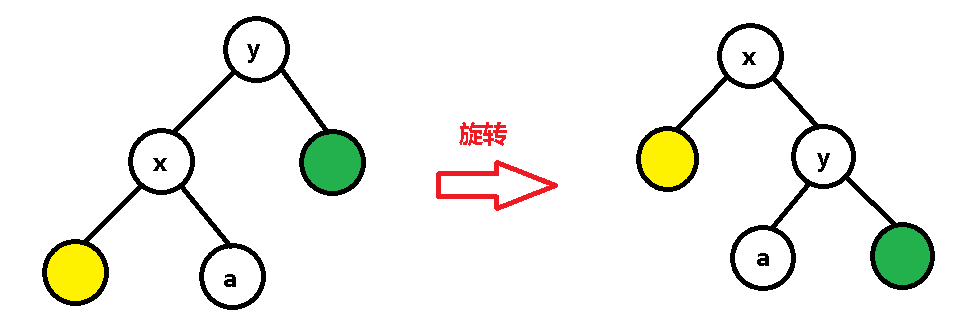
从上述的旋转过程中我们可以得出一些规律:
1. 黄点之前作为旋转点 x 的左儿子,旋转之后还是 x 的左儿子;绿点之前作为旋转点 x 的父亲 y 的右儿子,旋转之后还是 y 的右儿子;
2. 旋转点 x 是父亲 y 的左儿子的时候,那么如果 x 有右儿子,旋转之后要接到 y 的左儿子那里;反之如果旋转点 x 是父亲 y 的右儿子,如果 x 有左儿子,旋转之后要接到 y 的右儿子那里;
3. 旋转点 x 跑到了父亲 y 的地方;
4. 旋转点 x 的父亲 y 跑到了 y 的另一边儿子的地方;
根据上面总结的小规律,然后就可以具体推广一下下啦:
假如我们一开始并不知道 x 是 y 的左儿子还是右儿子,我们暂且设 x 是 y 的 b 儿子(b 代表左儿子或右儿子);
1. x 的 b 儿子旋转之后还是 x 的 b 儿子;y 的!b 儿子(另一边的儿子)旋转后还是 y 的 !b 儿子;
2. x 的 !b 儿子旋转后接到 y 的 b 儿子那里;
3. x 跑到 y 那里;
4. y 跑到 !b 儿子那里;
什么?你说万一 y 不是根结点怎么办。。。
好说啊!假设 y 的父亲是 z 吧,那么如果之前 y 是 z 的左儿子,旋转之后 x 就是 z 的左儿子;如果之前 y 是 z 的右儿子,旋转之后 x 就是 z 的右儿子(也就是说旋转操作和 z 没什么多大关系);
真的是脑子里面什么都有,说起来就。。。
体谅一下本蒟蒻的口才qwq,看不懂肯定是因为我没说清楚~
那就先看一下旋转操作的代码吧:
int fa[N],ch[N][2]; //ch[i][0]:i的左儿子,ch[i][1]:i的右儿子 int cnt[N]; //结点i的数出现了多少次 int data[N]; //结点i的权值 int siz[N]; //结点i及子树里有多少个数 int son(int x) //看x是他父亲的左儿子还是右儿子 { return x==ch[fa[x]][1];//左儿子返回0,右儿子返回1 } void pushup(int rt) //上传 { siz[rt]=siz[ch[rt][0]]+siz[ch[rt][1]]+cnt[rt]; //左右子树里的结点个数相加并加上当前结点的个数 } void rotate(int x) //旋转操作 { int y=fa[x],z=fa[y]; //这里y不一定有父亲,也就是说z可能为0 int b=son(x); //x是y的b儿子,ch[y][b]=x int c=son(y); //y是z的c儿子,ch[z][c]=y int a=ch[x][!b]; //找x逆儿子a if(z) ch[z][c]=x,fa[x]=z; //在原来y的位置换上x else root=x; //如果y没有父亲,说明y就是根,那么旋转后x就是根 if(a) fa[a]=y; //如果a存在,那就把它接到y下面 ch[y][b]=a; //x的逆儿子!b跑到了y的b边 ch[x][!b]=y; //原来x在y的b边,旋转之后y在x的!b那里 fa[y]=x; //y变成了x的儿子 pushup(y); //上传一下 pushup(x); }
Splay的伸展:
如果当前点,父亲,爷爷呈一条直线,我们先转父亲再转自己。
如果当前点,父亲,爷爷扭曲,我们连续转两次自己。
这个东西好像就是要把一个结点 x 旋转到某一层上去吧~
直接看代码(这个好理解多了):
void splay(int x,int i) //Splay操作,我们将x旋转到i的下面(将x旋转成i的儿子) { while(fa[x]!=i) //如果一直没转成i的儿子就一直转 { int y=fa[x],z=fa[y]; //y是x的父亲,z是y的父亲 if(z==i) //如果i是x的爷爷的话 { rotate(x); //我们直接再转一次x就是i的儿子了 } else { if(son(x)==son(y)) //如果x,y,z同线(同为左孩子或同为右孩子) { rotate(y);//先旋转一下y rotate(x);//在旋转一下x } else { rotate(x);//旋转两下x rotate(x); } } } }
插入一个结点(这个和 BST 很相似,也很好理解):
void insert(int &rt,int x) //插入一个结点 { if(rt==0) //原树里没有这个数,我们要新建结点 { rt=++nn; //nn是结点个数 data[rt]=x; //赋值 siz[rt]=cnt[rt]=1; return; } if(x==data[rt]) //如果插入的这个数在树种出现过了 { cnt[rt]++; //这个数的数量加一 siz[rt]++; //子树内结点个数加一 return; } if(x<data[rt]) //要插入的这个数比当前结点小 { insert(ch[rt][0],x); //往左子树里面插入 fa[ch[rt][0]]=rt; //tr的左儿子的父亲是rt,这里顺便初始化一下 pushup(rt); //更新一下rt的siz } else { insert(ch[rt][1],x);//否则就要往右子树里面插入 fa[ch[rt][1]]=rt; //rt的右儿子的父亲是rt,这里顺便初始化一下 pushup(rt); //更新一下rt的siz } }
删除一个权值为 x 的数:
void del(int rt,int x) //删除值为x的结点 { if(data[rt]==x) //我们找到了这个结点,准备删除它 { if(cnt[rt]>1) //如果结点不只一个,减掉一个就好了 { cnt[rt]--; siz[rt]--; } else //如果只有一个 { splay(rt,0); //将我们要删除的这个rt结点旋转到根结点(根结点的编号是0) int p=getmn(ch[rt][1]); //求出大于rt的最小的数(方法是找出右子树的最小值) if(p==-1) //如果发现右子树里没有左儿子的话,那么右儿子就是最小的 { root=ch[rt][0]; //让右儿子作为新树的根 fa[ch[rt][0]]=0; //左儿子接到右儿子下面,就是根的儿子 } else //如果有左儿子 { splay(p,rt);//先将这个最小值旋转到当前结点的儿子那里 root=p; //最小值作为新根 fa[p]=0; ch[p][0]=ch[rt][0]; //将当前结点的左儿子接到最小值下面 fa[ch[rt][0]]=p; pushup(p); //更新一下根结点的siz } } return; } //熟悉的寻找x的过程 if(x<data[rt]) //如果x小于当前结点就走左子树 { del(ch[rt][0],x); } else { del(ch[rt][1],x); //否则走右子树 } pushup(rt); }
找最小值(这个和 BST 一毛一样,方法就是一直走左子树):
int getmn(int rt) //找最小值 { int p=rt,ans=-1; while(p) { ans=p; p=ch[p][0]; //有左儿子就一直走左儿子 } return ans; }
找 x 的前驱:
int getpre(int rt,int x) //算x的前驱,前驱是最大的比x小的数 { int p=rt,ans; //p是当前结点编号,ans是x的前驱 while(p) { if(x<=data[p]) //如果x比当前结点小,走左子树 { p=ch[p][0]; } else //否则就走右子树 { ans=p; //随着我们一直往下往右找,找到的前驱一定是越来越优的 p=ch[p][1]; } } return ans; }
找 x 的后继:
int getsuc(int rt,int x) //找x的后继,后继就是最小的大于x的数 { int p=rt,ans; while(p) { if(x>=data[p]) //比当前结点大走右子树 { p=ch[p][1]; } else //否则走左子树 { ans=p; //随着我们一直往下往左走,找到的后继一定越来越优 p=ch[p][0]; } } return ans; }
找排名第 k 的数是几:
int getkth(int rt,int k) //求排名第k的结点 { int l=ch[rt][0]; //当前结点的左儿子 if(siz[l]+1<=k&&k<=siz[l]+cnt[rt]) return data[rt]; //如果比左子树的个数多但是却又比加上该结点后的个数少,那么不就是第k名元素就是当前结点 if(k<siz[l]+1) return getkth(l,k); //比左子树的个数少的话就在左子树里 else return getkth(ch[rt][1],k-siz[l]-cnt[rt]); //否则就在右子树里 }
求权值为 k 的数排名第几:
int getk(int rt,int k) //求权值为k的结点排第几 { if(data[rt]==k) //我们找到了这个结点 { splay(rt,0); //把它转到根的位置,这样的话左儿子个数+1就是它的排名 if(ch[rt][0]==0) //如果没有左儿子,它就排第一 { return 1; } else //如果有左儿子 { return siz[ch[rt][0]]+1; //排名为:左儿子个数+1 } } //又是熟悉的查找过程 if(k<data[rt]) return getk(ch[rt][0],k); //比当前结点小就走左子树 if(data[rt]<k) return getk(ch[rt][1],k); //比当前结点大就走右子树 }
splay其实理解透了就很简单了哦~ 建议先看一下C++提高组一本通的 Treap 部分再来食用效果更佳哦~
然后就没了鸭QwQ~

