7月清北学堂培训 Day 2
今天是林永迪老师的讲授~
继续昨日的贪心内容。
我们继续看例题:

分析样例的过河方法:
首先1和2先过河,总时间为2;
然后1回来,总时间为3;
然后5和10过河,总时间为13;
然后2回来,总时间为15;
然后1和2过河,总时间为17;
一个很强烈的贪心思路:最慢和次慢的两个人一定要一起过河;
证明:
假设我们有四个人 A B C D,他们过河时间是依次增大的。
假如我们有两种过河的方案:
1.让过河最快的人A来回将三个人送过河:AC + A + AD + A + AB;
2.先让最快的两人A和B过河,对面最快A的回来,C和D一起过河,然后最快的B回来,然后A和B一起过河(样例的方法):AB + A + CD + B + AB;
那么第一种方案所需的时间是: C + A + D + A + B = 2 * A + B + C + D;
那么第二种方案所需的时间是: B + A + D + B + B = A + 3 * B + D;
经比较显然大多数情况下第二种方案更优,所以我们要让 C和D 一起过河。
那么我们就有了一个贪心思路:先让最快和次快的人先过河,然后最快的回来,最慢和次慢的过河,次快的再回来,这时候我们发现只有最慢和次慢的过河了,其他人还没动,原来的n个人变成了n-2个人,这不就是原问题的子问题嘛?我们仍然按照上面的贪心思路走,那么最后一定会只剩下3人或4人,对于四个人的情况,还是按照上面的贪心思路,对于3个人的情况,我们另外讨论一下:
我们还是有 A B C 三人,他们过河的时间依次增大,无非也就下面两种过河情况:
1. A 和 B 过河,A 回来,A 和 C 过河:AB + A + AC;
2. B 和 C 过河,B 回来,A 和 B 过河:BC + B + AB;
第一种方案所需的时间是:A + B + C;
第二种方案所需的时间是:2 * B + C;
显然第一种情况更优哦~
那么这个题不就做完了?
贪心骗分导论:
我们有一种搜索叫作 k搜索,我们搜索的时候就是在遍历搜索树的过程,因为贪心是找最优解的过程,那么我们在遍历搜索树的时候走最优的儿子;但这样的话往往是错的,所以我们可以尝试搜一搜次优解,再可以搜一搜次次优解,简单地说就是有限制步数的深度搜索(迭代加深搜索);
分治算法
分治分治,分而治之,分治算法就是讲一个大问题划分成几个规模更小的问题并加以解决,通过解决子问题最终解决总问题。
分治算法在OI中的运用主要在两个方面:
1.基于二分查找,三分查找的运用;
2.将题目划分成更细小的子问题运用;
二分的本质求的是边界!在一个有序区间内确定一个边界,在边界的一边的元素满足某种性质,而另外一边不满足;
故二分经常用于解决如下类型的问题:
1.简单的二分查找;
2.二分答案(即求一个单调函数在满足某个性质下的最值);
3.最值的最值(最小化最大值,最大化最小值),这也是最常见的二分题类型;
它面对的一定是有序的,这个有序可以指大小或某种性质。
首先你可能需要个好的模板:

例一:

一道经典的线段树题,对于每个订单我们都查询一下区间最小值,看看是否和dj 相同。
我们可以画一个时间轴,上面的每个数表示当天需要借出多少个教室,如果有个订单要从sj ~ tj 借 dj 个教室,那么我们将区间 [ sj , tj ] 每个数加上 dj ,那么我们可以用差分啊QwQ~就可以维护前缀和来求出当天需要多少教室;由于如果出现第一份订单不满足的话你们后面的订单也不会满足的,而前面都是满足的,这就和二分前提很类似啊,所以我们可以二分订单数量,时间复杂度为严格的O(nlog n);

例二:

最大自然数最小,就意味着我们要二分答案:
我们二分答案 v,尝试将 1~v 内的自然数分配给 a 和 b,我们可以先把被 x 整除的数但不被 y 整除的数给 b,把被 y 整除但不被 x 整除的数给 a。然后剔除所有被 x*y 整除的数,剩下的数与 x 和 y 都互素,判一下能不能好好的分配就可以了。
inline bool check(long long num) //检查我们枚举的num是否能给够 { long long u=num/x; //能被x整除的数的个数 long long v=num/y; //能被y整除的数的个数 long long w=num/(x*y); //能被(x*y)整除的数的个数 long long c1=cnt1,c2=cnt2; //当前我们还差c1个数就给够A,还差c2个数就给够B c1-=v-w;c2-=u-w; //将是y的倍数却不是x的倍数的给A,将是x的倍数却不是y的倍数的给B if(c1<0) c1=0; //如果给多了不能是负数啊,得弄成0 if(c2<0) c2=0; if(c1+c2>num-u-w+w) return 0; //如果不够的话,增大枚举的num return 1; //够了,往小里枚举试试 }
安利一下几个做题网站:
CodeForce
CodeChef
TopCoder
三分
三分的难度要低于二分(因为变换出来的花样少)
三分的用处在于求一个单峰函数的最值;
单峰函数,例如:
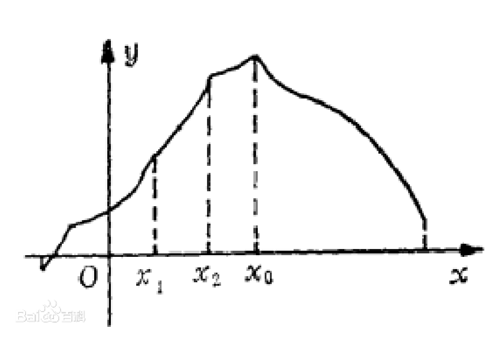
我们每次取这个函数的 1/3 和 2/3 处,比较两个分界,舍去次优的那个点以下的部分;
例如我们要求下面这个函数的最大值,我们先三分找到两个分界点P1,P2:
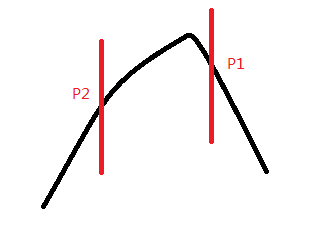
我们发现P1的值比P2的值要大,那么我们就舍弃P2以下的那一部分:
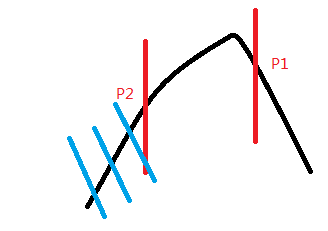
我们这样一直三分下去就好了,直到找到最优解,时间复杂度是O(log3 n);
三分代码:

实数比较:
double eps = 1 e -8(精度)
先将 a 和 b 做个差,如果这个差值小于 eps ,那么说明 a 和 b是相同的;如果差值小于0,说明 a<b;
如果不是单峰函数怎么办?
把这个函数割成若干个单峰函数:

分块
分块算法相当于是一个对于线段树和树状数组算法的下为替代品,由于其算法简单粗暴十分好写故广泛地运用于骗分领域QwQ~
分块就是好几个小数组以块的形式连起来,每个块的大小是由你事先设好的。
看一个问题:

第一问:
我们可以用分块做,设置每个块的大小为√n,有如下三种情况:
1. l 和 r 在同一个块里,那么我们直接暴力跑就好了,时间复杂度不超过√n;
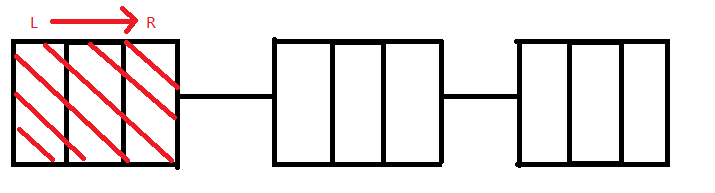
2. l 和 r 在相邻的块里,这时候我们还是暴力枚举,时间复杂度不超过2 * √n;

3,.l 和 r 隔得很远,这时候我们先暴力出 l 和 r 当前块里的数加上某个数,然后在中间的所有块里打上标记,表示这个块里每个数都加上Tag;

第二问:
还是用分块,我们将每个块里面的数排个序:
1. l 和 r 在同一个块里,那么我们直接暴力跑就好了,时间复杂度不超过√n;
2. l 和 r 在相邻的块里,这时候我们还是暴力枚举,时间复杂度不超过2 * √n;
3. l 和 r 隔得很远, 我们将每个块里的元素排序,存到一个 b 数组里面:
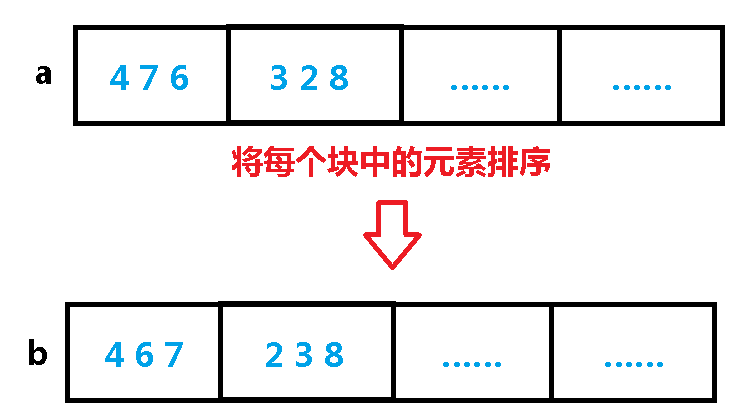
这样的话,我们在查询的时候只需要在 a 数组中左端点所在的格子暴力枚举一下右边有多少个数符合条件,在右端点所在的格子里暴力枚举左边有多少个数符合条件,对于中间的格子,我们直接在 b 数组里面二分查找第一个小于等于 x 的数就好了;
第三问:
因为 264 最多开方 6 次就变成 1 了,因为√1 =1 , √0 = 0,所以无论开多少次都是不变的,如果我们发现一个块里的数不是1就是0,那么我们就可以给这个块打个标记说明这个块已经成熟了,不用再管它了QwQ~
时间复杂度不会超过O(6n);
例一:

我们先开两个数组:
color [ i ]:表示下标为 i 的球的颜色;
pre [ i ]:前一个颜色为 color [ i ] 的球的下标;
如果我们询问区间 [ l , r ] 的答案的话,那么有以下两种情况:
1. 一种颜色 color [ i ] 的上一个相同颜色的位置 pre [ i ] 在这个 [ l , r ] 的区间里:

由于这种颜色在这个区间内出现了多次,所以我们暂且不管这个颜色;
2. 一种颜色 color [ i ] 的上一个相同颜色的位置 pre [ i ] 不在这个 [ l , r ] 的区间里:
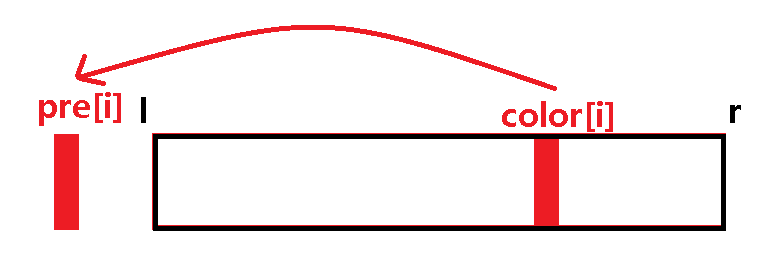
这也就是说,这种颜色的上一个相同颜色不在这个区间里了,说明这个颜色在区间中是最后一个出现的了(也可以通俗地理解成这种颜色在这个区间内只出现了一次),那么颜色数++;
那么答案不就是找所有的 pre [ i ] 在区间外的颜色?即 pre [ i ] < l;
有同学就要问了,第一种情况为什么不记录上?
Answer:请看下面这张图:
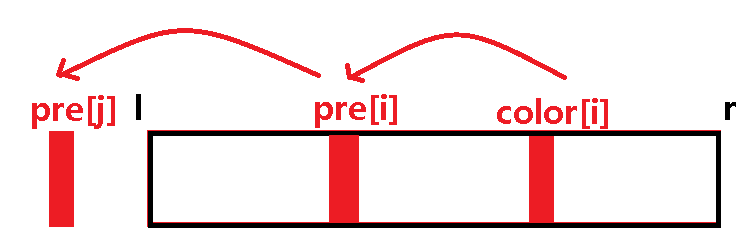
当前我们找到了 color [ i ],发现它前面的 pre [ i ] 也在这个区间里,这时候我们就不用再管它了;因为我们接着往前扫的时候,一定会找到这个 pre [ i ],这时候我们发现它的前一个颜色相同的位置是 j,在区间以外,我们使颜色数++;这样我们就实现了既不选上同一个颜色也不漏选的情况;
搜索
搜索算法不是灵丹妙药,也不是万金油;
搜索,启发式搜索,动态规划,最短路算法之间的关系;
搜索树的概念以及四种基本搜索算法的适用情况;
1.深度优先搜索;
2.广度优先搜索;
3.双向广度优先搜索;
4.迭代加深搜索;
深度优先搜索
外号:深搜,电风扇,大法师,回溯;
是欺骗自己的好东西(滑稽);
较多用于走迷宫和树的遍历中(以及大名鼎鼎的网络爬虫);
虽然要利用栈进行递归但是不可思议的空间依旧比广搜小,深搜的空间是O(深度)级别的,广搜的空间是O(个数)级别的;
一般结合强力的剪枝服用时有奇效;
由于不需要搜索完所有的节点也能出一些结果,故在骗分界有广泛好评;
在寻找最优解的问题上基本被广搜吊打;
广度优先搜索
杀人放火,居家必备,解决最优性问题有两把刷子;
擅长答案在搜索树比较浅的位置时的情况;
虽然名字叫广度优先搜索,但其实并不喜欢很宽的搜索树;
状态的表示并没有深度来的舒服;
并没有很好的剪枝策略,垃圾结点一大堆;
空间上完全被锤爆了,可以说是一点都没有考虑过内存的想法;
双向广搜
当你知道起点和终点时就可以使用的操作,能大大减少广搜扩展到垃圾结点,不过就算这样内存依旧表示很不友好;
总的一句话,比广搜只好不差(当然代码量除外);
其实是有双向深搜和双向 A*,然鹅并木有什么卵用;
迭代加深搜索
算是广搜向内存妥协后的奇葩产物,骚气地结合了深搜和广搜的特点(大雾;
迭代加深搜索在面对庞大的搜索树时往往表现出了值得信任的优异表现;
其实也是有迭代加宽搜索的,不过价值和它给人的第一印象一样不靠谱就是了;
搜索剪枝
没有剪枝的搜索就像是没有跳刀的斧王
常用的剪枝主要有一下几种:
1.可行性剪枝;
2.最优性剪枝;
3.记忆化搜索;
4.搜索顺序以及代码细节;
5.启发式剪枝;
其实做题时想不想得到全靠脑洞,有没有效果全看缘分(大雾;
例一:

首先不加任何剪枝的dfs应该长这个样子:

可行性剪枝:
如果我们求的蛋糕体积以及大于题目给出的体积,那么就返回;
最优解剪枝:
求表面积的过程中,如果求出的S不如答案优,那就返回;
剪枝一:如果在搜索的过程中体积小于0 或者当前半径或高度小于剩余要制作的层数(因为每层必须是相差1的,当前半径或高度小于要制作的层数,肯定不能制作完)就要剪枝.
剪枝二:当前剩下m层需要制作,可以预测制作这m层蛋糕最少需要多少体积,如果这个最少的体积还大于当前剩余的体积,那个这个不必继续搜索,所以要剪枝。
剪枝三:因为要求求最小表面积,如果当前枚举到的面积已经大于要求得的最优表面积,就要剪枝,但是这个剪枝还可以更优化,根据剪枝二的启发,如果当前枚举到的面积加上制作剩余m层蛋糕所要花费的最小表面积大于已经求得的最优解,那么剪枝。
剪枝四:因为体积必须为N,根据剪枝二,如果剩下m层蛋糕制作都按照最大的来,依然不能够使用完剩余的体积那么也要减掉。
数论
qbxt三次都讲到了,尤为可见其重要性!

高精度运算
高精度除法——高精除单精
void div(Bignum a,int b) //高精度除单精度,Bignum是个结构体 { int t=0; for(int i=a.size-1;i>=0;i--) { t=t*10+a.a[i]; //向高位借位当10用 a.a[i]=t/b; //作除法 t%=b; //剩下的数 } while(a[a.size-1]==0&&a.size>1) a.size--; //除去前导零 }
高精度除法——高精除高精

丧心病狂的 lyd 莫名其妙搞出来的高精度开方:

这是什么意思呢?
我们现在原数中找到小数点,然后分别往左往右找,每两个数就用一个逗号隔开,位数不足的用0补上:

先看第一组数 76,64<76<81,说明开方后整数部分是8,所以我们在76上面写个8,并用 76 减去 82 得到的数与第二组数结合起来:

我们就得到了一个新数 1254,我们继续求这个新数的开方数:
显然我们能列出这个式子来求开方:(10c+x)2 <=y(c是我们已经求出来的数,y是我们要开方的数),求最小的 x,将左边完全平方公式展开就是:100c2 + 20cx+ x2 <= y,我们将含 x 的那一项合并就是:100c2 + (20c + x)* x <=y,然后我们发现 100c2 就是我们两位两位拉下来的过程(超级雾,我们只用管后面的那一坨就好了。
将我们已经求出来的 8 乘上 20 变成 160 ,我们算(160 + x)* x <= 1254 的最大 x,由计算可知:(160 + 7)* 7 = 1169,那么第二位就是 7,我们在第二组数的上面写上 7,并用 1254 - 1169 得到的数与第三组数结合起来:
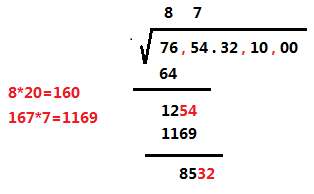
我们又得到了一个新数 8532,我们继续求这个新数的开方数:我们将我们已经求出来的 87 乘上 20 变成 1740,我们算(1740 + x)* x <= 8532 ,由计算可知:1744 * 4 = 6976,那么第二位就是 4,我们在第三组数的上面写上 4,并用 8532 - 6976 得到的数与第四组数结合起来:

快速幂
原理很简单,假设我们要算 35,考虑到 5 我们可以用二进制表示成:101,那么 5 = 22 + 20,代入就是:3(2^2 + 2^0)= 32^2 * 32^0;所以我们就可以先把 b 换成二进制,从后往前一位一位地看,这个当前这一位 i 是 1,ans 就乘上 a2^i:

矩阵快速幂
n×m 的矩阵乘上 m×r 的矩阵就会得到一个 n×r 的矩阵,其运算公式是这样的:
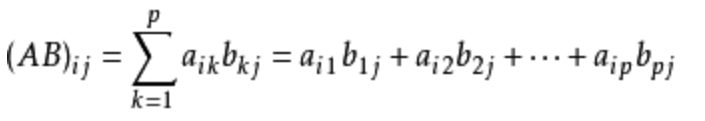
矩阵快速幂常用于求解线性递推方程组,例如斐波那契数列:
F(n)= F(n-1)+ F(n-2)
如果考虑递推的话时间复杂度是O(n),n如果到了1e9 以上的数据就直接死了;
那么我们就可以考虑用矩阵快速幂做!
我们先开一个 1 * 2 的矩阵:
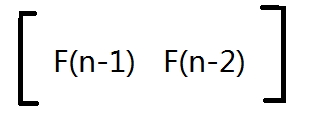
考虑怎么转移到下一个状态:

利用递推方程 F(n)= F(n-1)+ F(n-2),我们发现可以将其乘上这个 2 × 2 的矩阵(下面称之为“转化矩阵”)就可以转化到了:
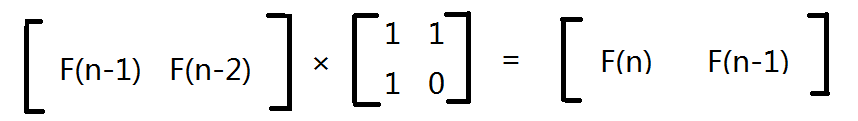
那么我们再乘一次会发生什么?看下面喽:
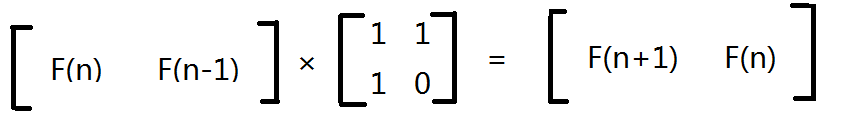
也就是说,我们每乘一下转化矩阵,我们斐波那契数列就求出了下一项。
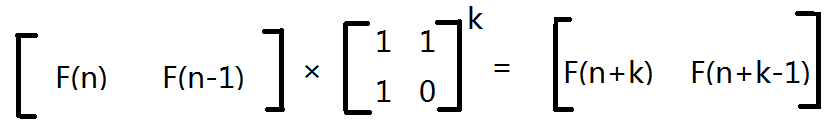
所以问题就变得很简单了,我们只需要将初始矩阵乘上转化矩阵的 n-1 次幂就能求出斐波那契数列的第 n 项了,这就是矩阵快速幂的应用:
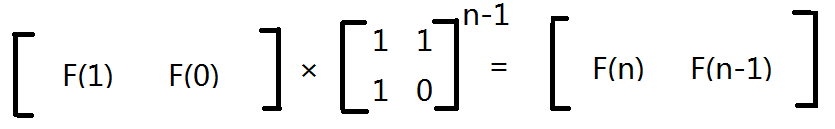
矩阵快速幂基于以下的原理,即可以找到一个矩阵 M,使得 [F(n-1) F(n)]T* M = [F(n) F(n+1)]T
以斐波拉期数列为例:M = ((1 1) (1 0));
以此类推:
[F(0) F(1)]T* Mn = [F(n) F(n+1)]T;
我们成功将一个递推式转化成了一个求矩阵幂的问题;
利用快速幂算法可以将时间缩短为 O(d3 log n);
利用 FFT + 矩阵特征多项式的黑科技可以把时间进一步缩短到 O(d logd logn);
我们来试着写一下下面的矩阵:
F(n) = 7F(n-1) + 6F(n-2) + 5n + 4 * 3n

从高斯消元到线性基
高斯消元是求线性方程组的方法,不懂的看这里哦 传送门;
高斯消元可以将一个矩阵变成一个上三角矩阵;
在 OI 中一般用于两点:求解线性方程组(不常见) & 求线性基(常见)
线性基常见问题:
如何求一堆数的异或和中第 K 大的值?
欧拉筛和积性函数
常见的埃拉托斯特尼筛,时间复杂度为O(nlog n),优化后为O(nlog log n);

考虑到筛 i 的倍数的时候可以直接从 i * i 开始筛,因为更小的倍数早已被筛过了,这样优化后时间复杂度就是O(n log log n);
欧拉筛
我们发现还是有一些数被多次筛过,例如 6 既被 2 筛过也被 3 筛过;
我们可以保证每个数只被它的最小质因子筛去,时间复杂度o(n);

#include<iostream> #include<cstdio> using namespace std; int read() { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<1)+(a<<3)+(ch-'0'); ch=getchar(); } return a*x; } int prime[10001],judge[10001]; //prime[i]:第i个质数是几 //judge[i]:i是不是合数 int n,tot; //求1~n以内的所有质数,其中质数个数是tot void getprime(int n) { for(int i=2;i<=n;i++) { if(!judge[i]) //如果不是合数,那么就是质数 { prime[++tot]=i; //记录一下 } for(int j=1;j<=tot;j++) //枚举所有的质数 { judge[i*prime[j]]=1;//倍数标记为合数 if(i%prime[j]==0) break; //如果是最小质因子,跳出 } } } int main() { cin>>n; getprime(n); for(int i=1;i<=tot;i++) cout<<prime[i]<<" "; //输出所有的质数 return 0; }
积性函数
积性函数:对于所有互质的 x 和 y,F(x * y) = F(x) * F(y)
完全积性函数:对于所有 x 和 y ,F(x * y) = F(x) * F(y)
常见的积性函数:
欧拉函数 φ(n) :不超过 n 与 n 互素的数的个数。
若 n = p1q1 * p2q2 * p3q3 * …… * pkqk ,则 φ(n) = n * ( 1 - 1/p1) * ( 1 - 1/p2 ) * ( 1 - 1/p3 ) * …… * ( 1 - 1/pk );
约数个数:( 1 + p1 ) * ( 1 + p2 ) * ( 1 + p3 ) * …… * ( 1 + pk );
约数和:( 1 + p1 + p12 + p13 + …… + p1q1 ) * …… * ( 1 + pk + pk2 + pk3 + …… + pkqk )
欧拉筛还可以用来维护一些复杂的函数值。
如:逆元、一个数的质因数分解中最大的指数的值。
怎么欧拉筛的时候求积性函数?
当我们筛 i 的时候,会选取一个素数p,将 p * i 筛掉,此时会检查 i 的最小质因子是不是 p,所以有两种可能:
1. i 和 p 互素; phi [ i * p ] = phi [ i ] * phi [ p ] (符合积性函数的性质);
2. i 的最小质因子刚好是 p; phi [ i * p ] = phi [ i ] * p;
说下第二个怎么来的吧:
我们可以将 i 分解:
i = p1q1 * p2q2 * p3q3 * …… * pkqk ,再看到 φ函数的计算式: φ(i) = i * ( 1 - 1/p1) * ( 1 - 1/p2 ) * ( 1 - p3 ) * …… * ( 1 - pk )
考虑到 (1 - 1/pi)= (pi - 1)/pi ,所以式子可以化简成:φ(i)= i * ( p1-1) / p1 * ( p2-1) / p2 * ( p3-1) / p3 * …… * ( pk-1) / pk;
然后我们将 i 的分解式代入:
φ(i)= p1q1 * ( p1-1) / p1 * p2q2 * ( p2-1) / p2 * p3q3 * ( p3-1) / p3 * …… * pkqk * ( pk-1) / pk
= p1q1-1 * ( p1-1) * p2q2-1 * ( p2-1) * p3q3-1 * ( p3-1) * …… * pkqk-1 * ( pk-1)
那么我们现在来考虑 i * p 的情况:
由于 p 是 i 的最小质因子,那么也就是说 p = p1,那么将 i * p 分解就是:i * p = p1q1+1 * p2q2 * p3q3 * …… * pkqk
套上面的φ函数公式就可以知道:φ(i*p)= p1q1 * ( p1-1) * p2q2-1 * ( p2-1) * p3q3-1 * ( p3-1) * …… * pkqk-1 * ( pk-1)
与上面的 φ(i)对比可知:φ(i*p)=φ(i)* p;
证毕!
所以我们在用欧拉筛素数时就可以顺便将φ函数求出来了。
#include<iostream> #include<cstdio> using namespace std; int read() { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<1)+(a<<3)+(ch-'0'); ch=getchar(); } return a*x; } int prime[10001],judge[10001],phi[10001]; //prime[i]:第i个质数是几 //judge[i]:i是不是合数 //phi[i]:求i的φ函数 int n,tot; //求1~n以内的所有质数,其中质数个数是tot void getprime(int n) { phi[1]=1; for(int i=2;i<=n;i++) { if(!judge[i]) //如果不是合数,那么就是质数 { prime[++tot]=i; //记录一下 phi[i]=i-1; //i是质数的情况,答案就是i-1 } for(int j=1;j<=tot;j++) //枚举所有的质数 { judge[i*prime[j]]=1;//倍数标记为合数 phi[i*prime[j]]=phi[i]*phi[prime[j]]; //i与prime[j]互质的情况 if(i%prime[j]==0) { phi[i*prime[j]]=phi[i]*prime[j]; //i与prime[j]不互质的情况 break; //如果是最小质因子,跳出 } } } } int main() { cin>>n; getprime(n); for(int i=1;i<=tot;i++) cout<<prime[i]<<" "; //输出所有的质数 cout<<endl; for(int i=1;i<=n;i++) cout<<phi[i]<<" "; return 0; }
一个有意思的问题:
n/1 + n/2 + n/3 + n/4 +……+ n/n ?

A star(A*)
启发式搜索相较于其他的搜索的优势在于引入了一个启发式函数 f ( x ) = g ( x ) + h ( x );
g* ( x ) : 从起点 S 到 x 的理论最近距离;(真实走的距离)
g ( x ) : 对起点 S 到 x 对于 g* ( x ) 的估计;(理想上的最近距离)
h* ( x ) : 从 x 到终点 T 的理论最近距离;(真实走的距离)
h ( x ) : 从 x 到终点 T 对于 f* ( x ) 的估计;(理想上的最近距离)
f*(x)= g*(x)+ h*(x);(从起点走到终点中间经过 x 的实际走的距离)
f(x)= g(x)+ h(x);(从起点走到终点中间经过 x 的理想最近距离)
当满足 f ( x ) <= f * ( x ) 时,总能找到最优解;
A* 的算法流程:
和 BFS 几乎一样,只是每次都弹出当前局面中 f ( x ) 最小的那个局面进行扩展;
——故需要维护一个优先队列,
——使用系统的 priority_queue<> 即可;
当 f ( x ) = g ( x ) + h ( x ) 中 h ( x ) = 0 即失去了启发式函数,则变为Breadth First Search;
当 f ( x ) = g ( x ) + h ( x ) 中 g ( x ) = 0 则变为 Best First Search;
广搜将点压进队列里,A*将点压进优先队列里;
A*是贪心先搜最优情况,最后搜最坏情况;
例一:八数码问题

我们先求出每个数字的曼哈顿距离相加,作为理想答案 h,但实际情况 h* 一定大于等于 h ;
我们在搜索的时候,要记录每个局面是否已经搜到过,所以我们要开 99 的数组?炸!
考虑用状压:我们将当前局面排成一行数字,然后我们可以用康托展开求出这个排列是 rank 几(这样就不会重了),开的数组最大是 9!= 362880 ,显然不会爆。
最后我们启发式搜索,按照 f 数组从小到大去搜索,如果搜到一个状态发现 h = 0(理想状态下到达目标状态还有0步),说明我们已经搜到了目标状态了,那么我们直接输出 g 就好了;
#include <cstdio> #include <cstring> #include <cstdlib> #include <queue> const int sizeofpoint=1024; const int sizeofedge=262144; int N, M; int S, T, K; int d[sizeofpoint], t[sizeofpoint]; struct node { int u; int g; inline node(int _u, int _g):u(_u), g(_g) {} }; inline bool operator > (const node & , const node & ); struct edge { int point; int dist; edge * next; }; inline edge * newedge(int, int, edge * ); inline void link(int, int, int); edge memory[sizeofedge], * port=memory; edge * e[sizeofpoint], * f[sizeofpoint]; std::priority_queue<node, std::vector<node>, std::greater<node> > h; inline int getint(); inline void dijkstra(int); inline int Astar(); int main() { N=getint(), M=getint(); for (int i=1;i<=M;i++) { int u=getint(), v=getint(), d=getint(); link(u, v, d); } S=getint(), T=getint(), K=getint(); dijkstra(T); if (d[S]==-1) { puts("-1"); return 0; } K+=S==T; printf("%d\n", Astar()); return 0; } inline bool operator > (const node & u, const node & v) { return (u.g+d[u.u])>(v.g+d[v.u]); } inline edge * newedge(int point, int dist, edge * next) { edge * ret=port++; ret->point=point, ret->dist=dist, ret->next=next; return ret; } inline void link(int u, int v, int d) { e[v]=newedge(u, d, e[v]); f[u]=newedge(v, d, f[u]); } inline int getint() { register int num=0; register char ch; do ch=getchar(); while (ch<'0' || ch>'9'); do num=num*10+ch-'0', ch=getchar(); while (ch>='0' && ch<='9'); return num; } inline void dijkstra(int S) { static int q[sizeofedge]; static bool b[sizeofpoint]; int l=0, r=0; memset(d, 0xFF, sizeof(d)), d[S]=0; for (q[r++]=S, b[S]=true;l<r;l++) { int u=q[l]; b[u]=false; for (edge * i=e[u];i;i=i->next) if (d[i->point]==-1 || d[u]+i->dist<d[i->point]) { d[i->point]=d[u]+i->dist; if (!b[i->point]) { b[i->point]=true; q[r++]=i->point; } } } } inline int Astar() { h.push(node(S, 0)); while (!h.empty()) { node p=h.top(); h.pop(); ++t[p.u]; if (p.u==T && t[T]==K) return p.g; if (t[p.u]>K) continue; for (edge * i=f[p.u];i;i=i->next) h.push(node(i->point, p.g+i->dist)); } return -1; }
A*算法小结
可以说是相当实用了。
正确地选择股价函数以后速度飞一般地上升;
而且吃透了A*,你会发现他也没比BFS难写到哪里去(当然前提是你掌握了priority_queue的正确姿势)
但是……A*的缺点嘛,大概?相比于 BFS 只优不劣!!
所以不会A* 算法的同学要抓紧了啊。
IDA*
广搜通过迭代加深搜索来向内存妥协了,A*是否也能做同样的骚套路?
ID + A* = IDA*!
好吧……这些算法真会玩。。。
不过和A* 不同的是,启发式搜索在深搜中的运用更倾向于启发式剪枝。
g:从根结点下来几步;
h:还需要走几步;
如果 g + h > D,我们就直接返回;
双向A*?双向IDA*?
h(x)>h*(x)?
事实上h(x)与h*(x)的关系隐形决定了A*的运行速度与准确度。
逆元
听说不少没好好学数论的都死得挺难看的,比如下面这道题:

扩展欧几里得算法有什么用?——计算逆元!
逆元的定义:如果 x 对 p 有一个逆元 y,则 x * y ≡ 1 (mod p);
x 对一个数 p 有逆元当且仅当 (x, p) = 1;
由裴蜀定理:存在 a, b 满足:ax + bp = 1;
嗯……,等等,岂不是 ax ≡ 1 (mod p)

逆元有什么用?
我们可以用它来代替除法!
在取模的意义下做除法:
a / b 在模 p 的意义下等于 a * (b 对于 p 的逆元)
一:同余方程 ax ≡ b (mod p)
二:计算组合数取模
问题1、如何计算 1! ~ n! 对 P 的逆元?
问题2、如何计算 1 ~ n 对 P 的逆元?
给个结论:令 P = nt + k,则 n-1 = nt2 * f(k)2 (mod P),f(k)是 k 的逆元;
证明:
∵ P = nt + k
∴ nt ≡ -k (mod P)
两边同乘 k 的逆元:
nt * f(k)≡ -1 (mod P)
两边同时平方:
n2t2 * f(k)2 ≡ 1(mod P)
两边同乘 n 的逆元:
n-1 ≡ nt2 * f(k)2 (mod P)
证毕!
中国剩余定理
问题、求余方程组 x = ai (mod pi)
不多说,背代码:
令 P = p1 * p2 * ... * pn
令 Pi = P / pi
令 Qi = Pi 对 pi 的逆元
则 x = Σ(ai * Pi * Qi)


