P2401 不等数列

原题链接 https://www.luogu.org/problemnew/show/P2401

第一眼看觉得是暴力，草草得估了一下下时间复杂度：O（n * n！），显然不行。

考虑DP。

我们设：dp [ i ][ j ] 为序列中有 i 个数，其中满足 j 对 '<' 关系；

考虑边界情况

当我们的序列是从大到小排列时，无论序列里有多少个数，都是满足 '>' 关系，不满足 '<'关系；

换句话说，也就是使得序列全都不满足 '<' 关系的情况也就一种排列；

那么我们就得出了边界条件：

    for(int i=1;i<=n;i++)     //当前序列里有i个数 
        dp[i][0]=1;           //只能从大到小排好，就一种情况

考虑状态转移方程

假设我们的序列里已经排好了 i-1 个数，我们当前正在插入第 i 个数，考虑我们可以往哪里插入：

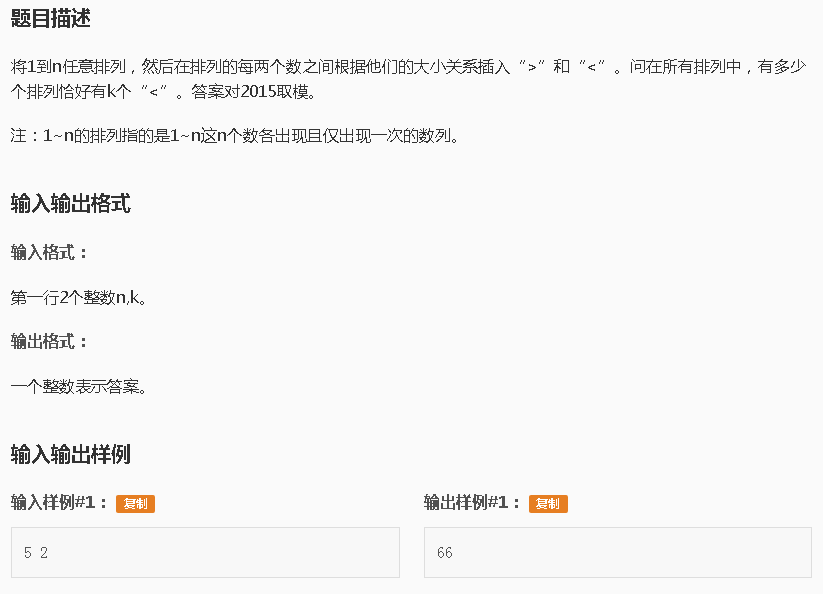
加入我们已经将X1~X5排好了，它们的关系是这样的：

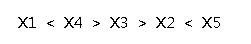
（A）现在我们考虑插入一个X6，我们可以插在这个序列的最后边，那么就会变成这样子：

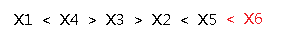
（B）当然我们也可以插入到最前面，那么就是介个样子：

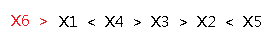
然后就是插在序列中间的情况，还要细分：

（C）1.插在小于号的位置：

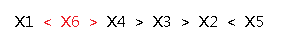
（D）2.插在大于号的位置：

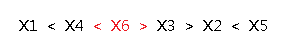
我们发现（A）和（D）这两种插法都会使得原序列多一个小于号，而（B）和（C）不会使原序列多一个小于号。

所以我们dp [ i ][ j ] 就可以从 dp [ i-1 ][ j-1 ] 和 dp [ i-1 ][ j ] 转移过来了，分别对应的是增加一个小于号和不增加小于号的情况；

怎么转移呢？先考虑 dp [ i-1 ][ j-1 ] 怎么转移过来： 

序列中已经有了 i-1 个数，说明有 i-2 个符号（'<' 或 '>'），其中有 j-1 个'<'，那不就说明有（i-2）-（j-1）= i-j-1 个 '>'，我们要使这个数按照（A）和（D）的方式插入才能转移到 dp [ i ][ j ]，所以考虑到我们合法的插入位置有（i-j-1）+1 = i-j 个，根据乘法计数原理可知：产生的方案数为 dp [ i-1 ][ j-1 ] *（i-j）；

dp [ i-1 ][ j ]同理，我们要将其按照（B）和（C）的方式插入，i-1 个数，j 个'<'，合法的插入位置有 j+1 个，根据乘法技术原理可知：产生的方案数为 dp [ i-1 ][ j ] *（j+1）；

 

考试时的AC代码：

#include<iostream>
#include<cstdio>
using namespace std;
int read()
{
    char ch=getchar();
    int a=0,x=1;
    while(ch<'0'||ch>'9')
    {
        if(ch=='-') x=-x;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        a=(a<<1)+(a<<3)+(ch-'0');
        ch=getchar();
    }
    return a*x;
}
const int mod=2015;
int n,k;
int dp[1010][1010];
//DP吧这题 
//与其一个一个排序,不如看做是好几个数一个一个往里插入
//dp[i][j]:序列里有i个数,且数列里已经有j个'<'的方案数 
//最后答案就是:dp[n][k] 
int main()
{
    //freopen("num.in","r",stdin);
    //freopen("num.out","w",stdout);
    n=read();k=read();
    for(int i=1;i<n;i++)      //当前序列里有 
    {
        dp[i][0]=1;           //边界情况，只能从大到小排好
        for(int j=0;j<i;j++)  //枚举序列里有多少个小于号 
        {
            dp[i+1][j]=(dp[i+1][j]+dp[i][j]*(j+1)%mod)%mod;   //有(j+1)个空插入后使得原序列的小于号个数不变
            dp[i+1][j+1]=(dp[i+1][j+1]+dp[i][j]*(i-j)%mod)%mod; //i个数,只有i-1个符号,其中小于号有j个,大于号就有i-1-j,再加上最右边还有一个空 
        } 
    }
    printf("%d",dp[n][k]%mod);
    return 0;
}