P3958 奶酪
原题链接 https://www.luogu.org/problemnew/show/P3958
话说 j 让我从提高组的题里面选一个讲,翻了好久,终于找到了这道 水 好题QwQ~
先来看题目:




大体看一遍题,觉得这个题应该是搜索吧~
点开算法标签看看呗:

哇,搜索蒙对了,不过……我觉得是深度优先搜索 dfs。
其实深度优先应该是最快的。
首先,我们找出所有可以从下表面进入的球,然后深度优先搜一遍。一旦遇到一个点最高处高度 z + r >= h,就表示可以到上表面,退出。因为每个洞最多访问一次(只需要求是否能到达上表面,而不是最短步数),然后决定下一步的时候还需要O(n)的时间。所以总时间复杂度是O(n*t)。

我们看上面这个图再理解一下:
先在所有的空洞中找出联通底部的空洞(符合条件 z - r <= 0),然后沿着这个空洞往上 dfs ,直到所到达的空洞已经通向顶部(符合条件 z + r >= h),那么就不用再向上搜索了,否则就一直往上搜,直到遍历完所有的空洞。
代码实现
我们先设一个结构体来表示每个空洞球心的坐标:
struct dole { long long x,y,z; //分别表示球心的横坐标x,纵坐标y,竖坐标z //对于本题只需知道竖坐标z是指球心在奶酪中的高度即可 }a[1001];
一. dfs 的起点
根据上面的思路,我们 dfs 的起点应该就是连接奶酪底部的那几个空洞。
我们枚举每一个空洞,判断它是否通向底部即可。
for(int j=1;j<=n;j++) //枚举每个空洞 { if(a[j].z-r<=0) //判断通向底部的条件,感性理解一下 { vis[j]=1; dfs(j); //从此空洞开始dfs } }
欢迎来到我也不知道会不会TLE但就是要优化系列QwQ~
我们考虑优化:
优化一:由于本题求的是是否有解,而不是有几个解,所以当我们在之前已经搜到解得话,我们就不必再往下搜了,直接 break 即可;
但是你会发现几乎每组数据的答案都是“No”,也就是说在绝大多数情况下你都要遍历每个空洞,这样的话你的第一个优化就没有什么意义了,所以我们要接着优化;
优化二:回过头来看我们判断空洞是否通向底部的条件: if ( a[ j ] . z - r <=0 ),考虑到如果有 a [ j ] . z - r > 0 的话,那么对于更大的 z,那么也一定不会满足条件的;这就启发我们可以将所有空洞的 z 从小到大排个序,然后我们开始找,如果有一个空洞的 z 不满足条件,那么对于以后更大的 z 也一定不满足条件,这时我们直接 break 掉就好啦;
这是加上两层优化后的代码:
sort(a+1,a+1+n,cmp); //按照每个空洞的高度从小到大排序 for(int j=1;j<=n;j++) { if(bj) break; //如果已经找到了解,就不必再往下找了 if(a[j].z-r<=0) //判断是否通向底部的条件,感性理解一下 { vis[j]=1; dfs(j); //从此空洞开始dfs } else break; //以后的空洞也一定不满足了,直接break掉 }
二. dfs 的过程
确定了起点后,我们只要找与之相连通的空洞往上钻,直到钻到顶部。
question:怎么判断两个空洞是否连通?
answer:如果两个球的半径之和 ≥ 两个球球心的距离,那么两圆相交(切)。
证明(看图理解):
1. 当两球相切时,显然球心距离等于两倍的半径:

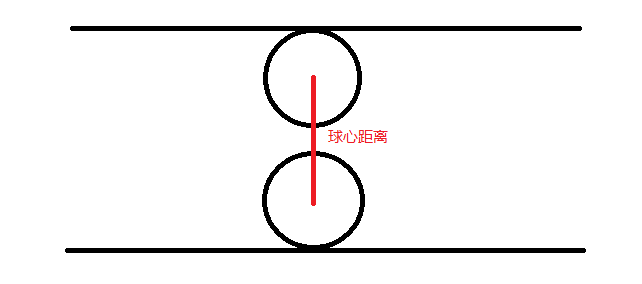
2. 当两球相离时,此时球心距离大于两倍的半径:
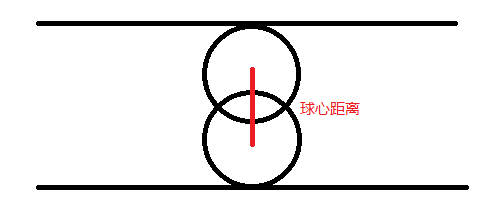
3. 当两球相交时,此时球心距离小于两倍的半径:
然后就可以贴 dfs 过程了:
double dis(long long x,long long y,long long z,long long xx,long long yy,long long zz) //求两球心的距离 { return sqrt((double)pow(x-xx,2)+(double)pow(y-yy,2)+(double)pow(z-zz,2)); } void dfs(int k) //当前搜到了第k个空洞 { if(a[k].z+r>=h) //判断是否到达顶部的条件,再感性理解一下 { bj=1; //标记有解 return ; } for(int i=1;i<=n;i++) { if(bj) return; //找到出口就不用再找了 if(dis(a[k].x,a[k].y,a[k].z,a[i].x,a[i].y,a[i].z)<=r*2.0&&!vis[i]) //判断两个空洞是否相连通 { vis[i]=1; dfs(i); //接着往下dfs } } }
三.答案输出
如果 bj =1 说明我们已经搜到解了,输出 Yes;否则输出 No ;
完整代码(辣么详细了应该都懂吧~):
#include<iostream> #include<cstdio> #include<cmath> #include<cstring> #include<algorithm> using namespace std; int read() //读入优化 { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } double dis(long long x,long long y,long long z,long long xx,long long yy,long long zz) //求两球心的距离 { return sqrt((double)pow(x-xx,2)+(double)pow(y-yy,2)+(double)pow(z-zz,2)); } long long t,n,h,r; //t组数据,n个空洞,奶酪的高度为h,每个空洞的半径为r long long x,y,z; //每个空洞的球心的坐标是(x,y,z) bool vis[1001],bj; struct dole { long long x,y,z; //分别表示球心的横坐标x,纵坐标y,竖坐标z //对于本题只需知道竖坐标z是指球心在奶酪中的高度即可 }a[1001]; bool cmp(dole x,dole y) { return x.z<y.z; //从低到高排序 } void dfs(int k) //当前搜到了第k个空洞 { if(a[k].z+r>=h) //判断是否到达顶部的条件,再感性理解一下 { bj=1; //标记有解 return ; } for(int i=1;i<=n;i++) { if(bj) return; //找到出口就不用再找了 if(dis(a[k].x,a[k].y,a[k].z,a[i].x,a[i].y,a[i].z)<=r*2.0&&!vis[i]) //判断两个空洞是否相连通 { vis[i]=1; dfs(i); //接着往下dfs } } } int main() { t=read(); for(int i=1;i<=t;i++) { memset(vis,0,sizeof(vis)); bj=0; n=read();h=read();r=read(); //n个空洞,奶酪高为h,每个空洞的半径是r for(int j=1;j<=n;j++) { a[j].x=read(); //空洞球心的坐标 a[j].y=read(); a[j].z=read(); } sort(a+1,a+1+n,cmp); //按照每个空洞的高度从小到大排序 for(int j=1;j<=n;j++) { if(bj) break; //如果已经找到了解,就不必再往下找了 if(a[j].z-r<=0) //判断是否通向底部的条件,感性理解一下 { vis[j]=1; dfs(j); //从此空洞开始dfs } else break; //以后的空洞也一定不满足了,直接break掉 } if(bj) printf("Yes\n"); else printf("No\n"); } return 0; }
不知道水的时间多不多QwQ~
更强的算法——并查集
这个算法的思路也是挺新颖,也挺好理解的QwQ~,下面就让我给大家讲讲思路吧:
对于每个空洞,我们需要先找出哪些空洞与顶部相通,哪些空洞与底部相通(条件就是上面刚说的,不用再讲了吧),然后枚举每个空洞找出所有与之相通的空洞,弄成一个父亲(明显并查集思想);最后我们再枚举每个与顶部相通的空洞和与底部相通的空洞,看看它们是不是一个父亲就好啦!
懂思路就好啦,不用再详细分析了,时间可能不大够了QwQ~
直接看代码吧(怕泥萌看不懂我附上了详细的注释,其实是题解第一篇啦):
#include<iostream> #include<cstdio> #include<cmath> #include<cstring> #include<algorithm> using namespace std; int read() //读入优化 { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } int f[1001];//并查集 int find(int x) { if (x!=f[x]) f[x]=find(f[x]); return f[x]; }//查找+路径压缩 double dis(long long x,long long y,long long z,long long xx,long long yy,long long zz) //求两球心的距离 { return sqrt((double)pow(x-xx,2)+(double)pow(y-yy,2)+(double)pow(z-zz,2)); } struct dole { long long x,y,z; //分别表示球心的横坐标x,纵坐标y,竖坐标z //对于本题只需知道竖坐标z是指球心在奶酪中的高度即可 }a[1001]; bool bj; long long t,n,h,r; //t组数据,n个空洞,奶酪的高度为h,每个空洞的半径为r long long x,y,z; //每个空洞的球心的坐标是(x,y,z) int top_num,bottom_num; //分别表示与奶酪顶部和底部想通的空洞个数 int top[1001],bottom[1001]; //top记录与顶面相交的洞的序号 //bottom记录与底面相交的洞的序号 int main() { int t; t=read(); for(int i=1;i<=t;i++) { n=read();h=read();r=read(); //n个空洞,奶酪高为h,每个空洞的半径是r bj=0; int top_num=0; //记录与顶面相交的洞有几个 int bottom_num=0; //记录与底面相交的洞有几个 for(int j=1;j<=n;j++) f[j]=j; //并查集初始化,自己的父亲是自己 for(int j=1;j<=n;j++) { a[j].x=read(); //空洞球心的坐标 a[j].y=read(); a[j].z=read(); if(a[j].z+r>=h) //判断这个点是否与顶面相交 top[++top_num]=j; if (a[j].z-r<=0) //判断这个点是否与底面相交 bottom[++bottom_num]=j; for (int k=1;k<=j;k++) //枚举之前的洞是否与这个洞相交,如果相交则合并集合 { if (dis(a[j].x,a[j].y,a[j].z,a[k].x,a[k].y,a[k].z)<=2.0*r) //判断两空洞是否相通 { int f1=find(j); //合并父亲的操作 int f2=find(k); if (f1!=f2) f[f1]=f2; } } } for(int j=1;j<=top_num;j++) //判断和顶部相通的空洞与和底部相通的空洞是否为同一父亲 { for(int k=1;k<=bottom_num;k++) if(find(top[j])==find(bottom[k])) { bj=1; break; } if(bj) break; } if(bj==1) cout<<"Yes"<<endl; else cout<<"No"<<endl; } return 0; }


