P2119 魔法阵

原题链接  https://www.luogu.org/problemnew/show/P2119

 

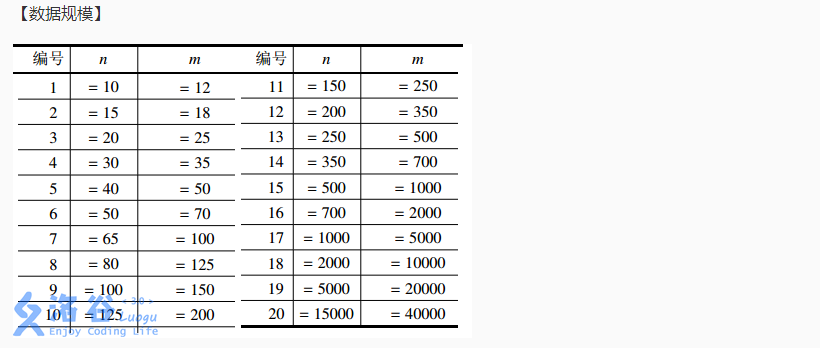
YY同学今天上午给我们讲了这个题目，我觉得她的思路很好，特此写这篇博客整理一下。

50分：暴力枚举

四重 for 循环分别枚举每个物品作为A物品，B物品，C物品，D物品的情况，看看能否满足题目中给出的三个式子，满足的话对应物品的次数加一就好啦；

100分：数学做法

我们回过头来看上面的三个式子：

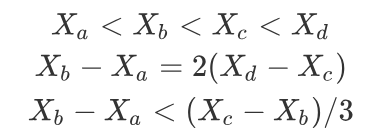
对于第一个式子，我们可以按照魔法值从低到高来选择物品；

由第二，三个式子我们可以得到：

 

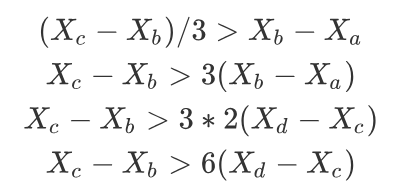
我们可以画一个数轴来表示物品A，B，C，D的位置，应该是长这个样子的（by YY）：

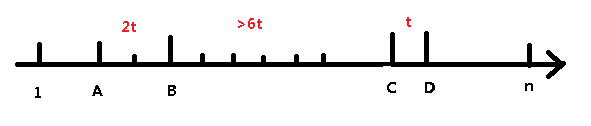
考虑枚举t

由于物品的魔法值只能取整数，所以通过上述的关系我们可以通过枚举 t 来求出魔法物品出现的次数。

考虑枚举范围：

考虑到AD>9t 且AD<=n，所以 9t < n；

 

我们已经知道AB=2t，CD=t，但是我们都不知道A，B，C，D的位置在哪里，那么怎么办呢？

我们可以分别枚举A和B中的一个，C和D中的一个，然后再利用上面的关系式求出另外一个；

考虑枚举D（这里是魔法值）

考虑枚举范围：

考虑到 A 最小为1，且AD>9t，所以D得位置要大于 9t+1，即我们要从 9t+2 开始枚举D；

有了D的位置，C的位置我们可以通过 D - t 推出来，但是由于 BC>6t，并没有具体的数值，我们还是不能确定B的位置；

又因为使A，B，C，D满足条件的k的最小值为1，所以对于当前的C和D，最大的A和B为A=D−9t−1，B=D−7t−1

那么如果A和B更小怎么办？

观察到在其他条件不变的情况下，只要C和B满足Xc−Xb>6t，那么这个魔法阵就一定成立，所以当(a1<a2，b1<b2)时，只要a2和b2能够和C，D组成魔法阵，a1，b1也一定能和C，D组成魔法阵，所以可以使用前缀和优化；

然后又由乘法原理可得，当前魔法值作为D物品的个数为SumD=SumA*SumB*SumC

所以我们利用前缀和优化SumA*SumB

C的情况可以顺便在算D的时候算出来

同理我们枚举A

但是和我们刚刚枚举D的情况也有些不同， 

在其他条件不变的情况下，只要C和B满足Xc−Xb>6t，那么这个魔法阵就一定成立，所以当(c1<c2,d1<d2)时，只要c1和d1能够和A，B组成魔法阵，c2，d2也一定能和A，B组成魔法阵，所以可以使用后缀和优化

因为需要统计后缀和，所以需要逆推

考虑枚举范围：

考虑到D需要<=n，而D>A+9t，所以A的最大上限就是：n - 9t -1；

因为需要逆推求后缀和，所以我们倒着枚举；

输出

输出的时候我们只需要输出第 i 个物品的魔法值作为物品A，B，C，D的次数就好啦；

特殊情况

因为我们的D>A+9t，而我们又知道A的最小值是1，t 的最小值是1，换过来就是：D>10，所以就是n最小得是11，要不然我们就找不到符合条件的D了；

#include<iostream>
#include<cstdio>
using namespace std;
int n,m,sum;
int A,B,C,D;
int num[15001],X[40001];
int a[40001],b[40001],c[40001],d[40001];
/*
a[i]魔法值为 i 的物品作为魔法阵的A物品的次数
b[i]魔法值为 i 的物品作为魔法阵的B物品的次数
c[i]魔法值为 i 的物品作为魔法阵的C物品的次数
d[i]魔法值为 i 的物品作为魔法阵的D物品的次数
*/ 
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++) scanf("%d",&X[i]),num[X[i]]++;
    if(n<11)                               //特判 
        {
            for(int i=1;i<=m;i++) 
                printf("0 0 0 0\n");       //无解的情况 
            return 0;
        }
    for(int t=1;9*t<n;t++)                 //t一定要在最外层 
    {
        sum=0;        
        for(D=9*t+2;D<=n;D++)              //顺着枚举D 
        {
            C=D-t;                         //算A,B,C 
            B=C-6*t-1;                     
            A=B-2*t;
            sum+=num[A]*num[B];            //维护前缀和 
            c[C]+=sum*num[D];              //算出C和D的情况 
            d[D]+=sum*num[C];
        }
        sum=0;
        for(int A=n-9*t-1;A;A--)           //同理倒着枚举A 
        {
            B=A+2*t;
            C=B+6*t+1;
            D=C+t;
            sum+=num[C]*num[D];
            a[A]+=sum*num[B];
            b[B]+=sum*num[A];
        }
    }
    for(int i=1;i<=m;i++) printf("%d %d %d %d\n",a[X[i]],b[X[i]],c[X[i]],d[X[i]]);  //输出对应得魔法值的次数 
}