P3368 【模板】树状数组 2

原题链接  https://www.luogu.org/problemnew/show/P3368

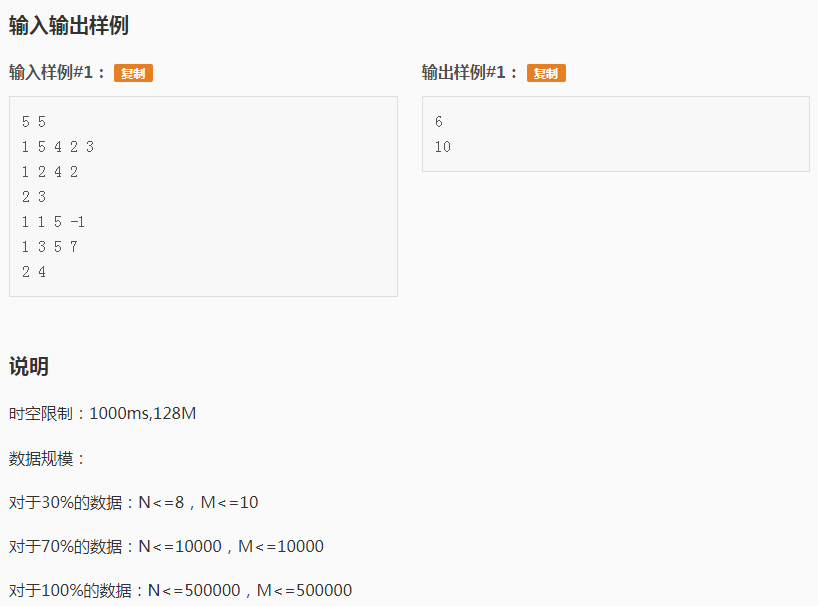
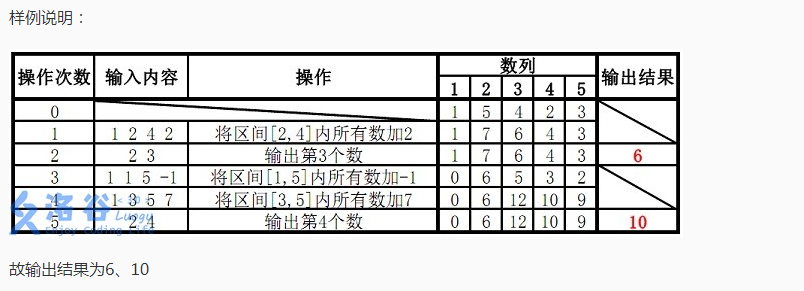
这个题和洛谷P3374树状数组1 有些不同，在普通的树状数组上运用了差分的知识。（由于P3374涉及到一些较为基础的知识，就先不讲了，反正大家都会了QwQ~）；

什么是差分呢？

差分差分，顾名思义就是相差的分数啦 ，其实就是每一项与前一项的差距，通常我们用d数组来表示。

举个例子，假如我们有一个序列：   

a₁=1，a₂=5，a₃=6，a₄=3，a₅=4；

那么可以计算出每一项的差分：

d₁=a₁ - a₀ =1 - 0 = 1；（第一项的差分就是原数）

d₂=a₂ - a₁ =5 - 1 = 4；

d₃=a₃ - a₂ =6 - 5 = 1；

d₄=a₄ - a₃ =3 - 6 = -3；

d₅=a₅ - a₄ =4 - 3 = 1；

有的小盆友就要问了：知道这个差分有啥用嘞？

这是树状数组“区间修改，单点查询”的关键！

考虑一个简单的小问题：知道了d_1~5，怎么求a₅？

It is so easy ！

a₅ = a₄ + d₅ = a₃ + d₄ + d₅ = a₂ + d₃ + d₄ + d₅ = a₁ + d₂ + d₃ + d₄ + d₅ = d₁ + d₂ + d₃ + d₄ + d_{5 ；}

也就是说，a_n= d₁ + d₂ + d₃ + ……+ d_n；

这一看不就是差分数组的前缀和嘛？正好我们可以用树状数组来维护前缀和：

void add(int x,int k)     //在第x个数上加个k
{
    for(int i=x;i<=n;i+=lowbit(i)) c[i]+=k;
} 

int ask(int x)            //询问区间[1,x]的和 
{
    int ans=0;
    for(int i=x;i;i-=lowbit(i))
       ans+=c[i];
    return ans;
}

又有小盆友来问了：不是你是用原数组求得差分，再用差分求回去，干啥嘞？只为了用树状数组维护前缀和？直接输出 a [ n ] 不好嘛？

其实这只是为了区间修改方便！

普通（暴力）区间修改思路：

for循环从l~r暴力枚举每个点然后加上某个值，最差的时间复杂度是O（q * n²），q是操作次数，这显然会TLE；

但是我们用了差分以后就不一样了，考虑一下区间修改后对差分数组的影响：

原先：

a： 1  5  6  3  4
d： 1  4  1  -3  1

在区间[3,5]上每个数都加上2：

a： 1  5   8   5   6
d： 1  4   3  -3   1

一个很显然的结论：对于修改的区间[ l，r ]，让这个区间内每个数加上x，对于差分数组d其实就是d[ l ] 加上x，d [ r + 1 ] 减去x（不懂的看上面的例子感性理解下）；

所以我们只需要用树状数组维护两次前缀和就好啦！

完整代码如下：

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int read()
{
    char ch=getchar();
    int a=0,x=1;
    while(ch<'0'||ch>'9')
    {
        if(ch=='-') x=-x;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        a=(a<<3)+(a<<1)+(ch-'0');
        ch=getchar();
    }
    return a*x;
}
int n,m,x,y,k,q;
int a[500001],d[500001],c[500001];
int lowbit(int x)
{
    return x&(-x);
}
void add(int x,int k)                    //在第x个数上加个k
{
    for(int i=x;i<=n;i+=lowbit(i)) c[i]+=k;  //加上lowbit去找它的父亲 
} 
int ask(int x)                           //询问区间[1,x]的和 
{
    int ans=0;
    for(int i=x;i;i-=lowbit(i))          //区间长度不断缩小 
       ans+=c[i];
    return ans;
}
int main()
{
    n=read();m=read();                    //n个数，m次操作
    for(int i=1;i<=n;i++)  
       {
           a[i]=read();
        d[i]=a[i]-a[i-1];                 //算出每一项的差分是多少 
        add(i,d[i]);                      //注意这里维护的是差分数组 
       } 
    for(int i=1;i<=m;i++)
    {
        q=read();
        if(q==1)
        {
            x=read();y=read();k=read();   //[x,y]加上k 
            add(x,k);                     //左端点差分+k 
            add(y+1,-k);                  //右端点的右边的差分-k 
        }
        else 
        {
            x=read();
            printf("%d\n",ask(x));          //差分前缀和，就是某一项的值 
        }
    }
    return 0;
}