2019.6.20 校内测试 NOIP模拟 Day 1 分析+题解
这次是zay神仙给我们出的NOIP模拟题,不得不说好难啊QwQ,又倒数了~
T1 大美江湖




这个题是一个简单的模拟题。 ----zay
唯一的坑点就是打怪的时候计算向上取整时,如果用ceil函数一定要先转化成double类型(话说我就这么掉坑里了?QwQ)
测试点 1: 0 次询问,所以直接freopen一下输出文件即可得分。期望得分 10 分。
测试点 4、5: 由于保证人物不移动,而且不捡拾出生点的物资也不在出生点打怪,所以攻击 防御一定全部为初始值,耗血一定为 0 ,直接输出 q 行数据即可。期望得分 20 分。
测试点 6、7、8: 地图上没有怪物,就不需要计算耗血那个复杂的式子,直接累加获得的药水即 可。期望得分 30 分。
测试点2、3、9、10: 考虑暴力模拟每一次行走,耗血的式子是可以 O(1) 计算的,而累加攻击防御 也是 O(1) 的,于是总复杂地 O(q),可以通过本题。期望得分 40 分。 需要注意的是在计算耗血的时候需要用到取整函数。如果使用 cpp 的 cmath 库里面的 ceil() 函数的话,需要注意括号里相除两数不能全为 int。
标程代码:
#include <cmath> #include <cstdio> #include <algorithm> const int maxn = 110; char mp[maxn][maxn]; int n, m, px, py, q; struct Character { int HP, ST, DE; int ehp, est, ede; void print() { printf("%d %d %d\n", this->HP, this->ST, this->DE); } void fight() { int x = int(ceil(1.0 * ehp / std::max(1, ST - ede))); this->HP += std::max(1, x * std::max(1, est - DE)); } void update(const char x) { switch (x) { case 'R': { this->HP = std::max(0, this->HP - 10); break; } case 'Q': { this->ST += 5; break; } case 'Y': { this->DE += 5; break; } case 'M': { fight(); break; } } } }; Character my; void mov(const int x); int main() { freopen("mzq.in", "r", stdin); freopen("mzq.out", "w", stdout); scanf("%d%d", &n, &m); for (int i = 1; i <= n; ++i) { scanf("%s", mp[i] + 1); } scanf("%d%d%d", &my.ehp, &my.est, &my.ede); scanf("%d%d", &px, &py); scanf("%d%d", &my.ST, &my.DE); scanf("%d", &q); int x; while (q--) { scanf("%d", &x); if (x == 1) { my.print(); } else { x = 0; scanf("%d", &x); mov(x); } } return 0; } void mov(const int x) { switch (x) { case 1: { --py; break; } case 2: { ++py; break; } case 3: { --px; break; } case 4: { ++px; break; } default: { puts("I AK IOI"); break; } }; my.update(mp[px][py]); }
我改完之后的代码:
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> using namespace std; int read() { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } int n,m,hp_e,st_e,de_e,st_m,de_m,hp_m; int x,y,q,cz,where; //从(x,y)开始走 char a[101][101]; int fight() { int ans=ceil(1.0*hp_e/(max(1,st_m-de_e))); //注意先转化成double类型 return max(1,(int)ans*max(1,st_e-de_m)); } int main() { freopen("mzq.in","r",stdin); freopen("mzq.out","w",stdout); n=read();m=read(); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) cin>>a[i][j]; //地图 hp_e=read(); st_e=read(); de_e=read(); x=read();y=read(); //从(x,y)开始走 st_m=read(); de_m=read(); q=read(); for(int i=1;i<=q;i++) { cz=read(); if(cz==1) //查询 printf("%d %d %d\n",hp_m,st_m,de_m); else //移动 { where=read(); if(where==1) y--; //向左走 if(where==2) y++; //向右走 if(where==3) x--; //向上走 if(where==4) x++; //向下走 if(a[x][y]=='.') continue; if(a[x][y]=='R') hp_m-=10; //回血 if(hp_m<0) hp_m=0; //小于10的话回到0 if(a[x][y]=='Q') st_m+=5; //加5攻击力 if(a[x][y]=='Y') de_m+=5; //加5防御力 if(a[x][y]=='M') hp_m+=fight(); //打怪 } } return 0; }
T2 腐草为萤




子任务 1: 只有一个点,所以只有 {1} 这一种集合,于是答案为 1。期望得分 5 分。
子任务 2、3: 爆搜,枚举所有可能的集合,然后计算答案。 由于每个点只有选进集合或不选两种可能,所以一共有 2 n 个集合,然后可以 O(n) 的去检验集合是否合法,顺便统计答案。于是总复杂度 O(2 n×n)。期望得分 25分。
子任务 4、5: 考虑 DP。设 fu 是以 u 为根的子树的答案。 如果 u 没有孩子,那么 fu = uT。 如果 u 只有一个孩子 v,那么要么选 u 不选 u 的子孙,要么不选 u。不选 u 的答案即为 fv,选 u 的答案即为 u T。两种情况加起来就是 fu。 如果 u 有两个孩子 x,y。考虑要么选 u,要么只选 x 的子树内的元素,要么 只选 y 的子树内的元素,要么既选 x 内的元素又选 y 内的元素但不选 u。前三种 情况的答案易得。现在考虑第四种情况的答案。设 s 是 x 子树内的某个集合。考 虑无论 y 的子树内怎么选,再加上 s 都是合法的,因为 y 和 x 之间没有祖先后 代关系且 s 在 x 之内。设 gu 是以 u 为根能选择的集合个数,那么一共有 gy 个 集合选择 s 以后依旧合法,设 s 的权值和为 ws,于是 s 的贡献即为 ws×gy。由于 fx 为 x 子树内所有可能集合的权值和,所以可以发现 ∑ws = fx 。于是 x 子树内 的集合对答案的总贡献是 fx×gy。同理,y 子树内的集合对答案的贡献是 fy×gy。 于是 fu=fy×gx+fx×gy+fx+fy+u T。gu=gx×gy+gx+gy+1。时间复杂度O(n),期望得分 30 分。
子任务6、7: 虑在遍历子节点的时候,已经遍历了一些子节点,现在新加入了一个子节点。 由于新加入一个子节点与之前遍历的子节点没有祖先后代关系,于是可以之前遍历 过得子树看成一棵子树,然后问题就变成了子任务4、5。期望得分 40 分。 需要注意的是由于读入规模达到了10e6左右,需要普通的读入优化。
标程代码:
#include <cstdio> typedef long long int ll; const int maxn = 1000005; const int MOD = 1000000007; template <typename T> inline void qr(T &x) { char ch; do { ch = getchar(); } while ((ch > '9') || (ch < '0')); do { x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar(); } while ((ch >= '0') && (ch <= '9')); } int n, T; int MU[maxn], frog[maxn], gorf[maxn]; bool vis[maxn]; struct Edge { int v; Edge *nxt; Edge(const int _v, Edge *h) : v(_v), nxt(h) {} }; Edge *hd[maxn]; void dfs(const int u); int main() { freopen("dzy.in", "r", stdin); freopen("dzy.out", "w", stdout); qr(n); qr(T); if (T) { for (int i = 1; i <= n; ++i) { MU[i] = i; } } else { for (int i = 1; i <= n; ++i) { MU[i] = 1; } } for (int i = 1, u, v; i < n; ++i) { u = v = 0; qr(u); qr(v); hd[u] = new Edge(v, hd[u]); hd[v] = new Edge(u, hd[v]); } dfs(1); printf("%d\n", frog[1] % MOD); return 0; } void dfs(const int u) { vis[u] = true; for (auto e = hd[u]; e; e = e->nxt) if (!vis[e->v]) { int v = e->v; dfs(v); frog[u] = (frog[u] * (gorf[v] + 1ll) % MOD) + (frog[v] * (gorf[u] + 1ll) % MOD); gorf[u] = (gorf[u] + gorf[v] + (1ll * gorf[u] * gorf[v])) % MOD; } frog[u] = (frog[u] + MU[u]) % MOD; ++gorf[u]; }
T3 锦鲤抄



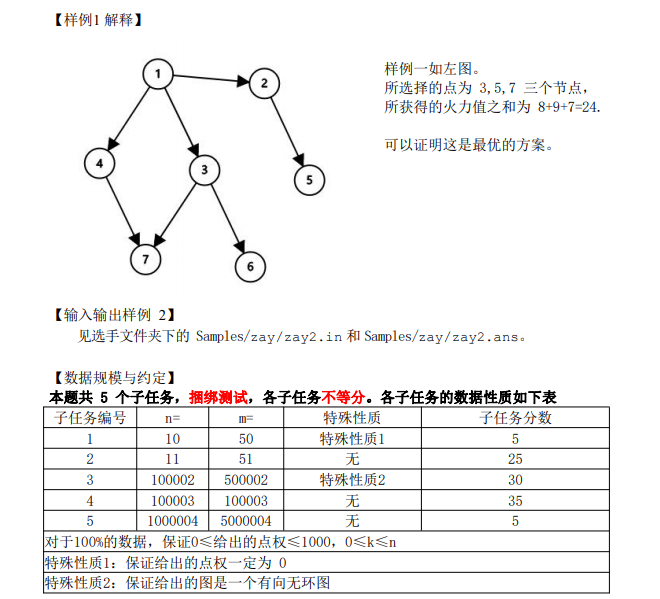

子任务 1: 点权都是0,于是无论怎么选答案都是 0,输出 0 即可。期望得分 5 分。
子任务 2: 爆搜,枚举所有可能的顺序,然后计算答案。 由于保证了数据随机,可以在搜索的过程中进行剪枝,效率很高,期望得分25 分。
子任务 3: 给出的是一个 DAG 。考虑对于一个 DAG 来说,一个良好的的性质就是在拓扑 序后面的点无论如何变化都无法影响到前面的点。这个题也一样。对于任意一个不 出现原图中本身入度为 0 的点的序列,只要按照拓扑序选点,就一定能取遍序列中 所有的点。 于是发现这张图上入度不为0的点事实上都可以被选择。于是我们把所有入度不 为0的点排一下序,求前k个就可以了。时间复杂度 O(nlogn),期望得分30。
子任务 4、5: 考虑DAG的情况放到普通有向图上会发生什么。 有了子任务 3 的提示,我们可以考虑把整个图缩点,将其变成一个DAG来做。 对于一个DAG,显然可以通过子任务 3 调整顺序的方式使得每个强连通分量的 选择情况除选点个数以外互不影响。故下面只讨论一个强连通分量内部的情况。 一个强连通分量显然可以看作是一棵外向树加上很多边得到的。 一棵外向树的定义:一个外向树的任意一个节点要么为叶节点,要么它与孩子 间的所有边都是由它指向孩子。 一棵外向树显然是一个 DAG 。按照之前对 DAG 上情况的说明,显然我们可以 选择除了根节点以外的任意节点。 因为一个强连通分量内部是互相连通的,于是我们不妨钦定一个点为根。 对于一个没有入度的强连通分量,我们不妨钦定点权最小的点为根。这样显然 选择的是最优的。 对于一个有入度的强连通分量,我们不妨钦定那个有入度的点为根。这样在选 择到只剩根节点的时候,因为根节点有入度,所以根节点是可以被选择的。于是这 个强连通分量可以被全部选择。这显然是最优的。 这样综合上述讨论,有入度的强连通分量可以随便选,没有入度的强连通分量 去掉最小的点权的点。剩下贪心取前 k 个就可以了。 进行一次 tarjan的复杂度是 O(n+m),选前 k 个点可以排序一下。这样总复杂 度 O(m+nlogn),期望得分 35 分。注意到复杂度瓶颈在排序上,考虑我们只需要前 k 大而不需要具体前 k 个之间的大小关系,于是使用 std::nth_element()函数可 以将复杂度降至 O(n+m)。期望得分 40 分。注意,输入规模到了 10e7 级别,需要 fread 来实现读入优化。
标程代码:
#include <cstdio> #include <algorithm> #include <functional> #ifdef ONLINE_JUDGE #define freopen(a, b, c) #endif typedef long long int ll; namespace IPT { const int L = 1000000; char buf[L], *front=buf, *end=buf; char GetChar() { if (front == end) { end = buf + fread(front = buf, 1, L, stdin); if (front == end) return -1; } return *(front++); } } template <typename T> inline void qr(T &x) { char ch = IPT::GetChar(), lst = ' '; while ((ch > '9') || (ch < '0')) lst = ch, ch=IPT::GetChar(); while ((ch >= '0') && (ch <= '9')) x = (x << 1) + (x << 3) + (ch ^ 48), ch = IPT::GetChar(); if (lst == '-') x = -x; } const int maxn = 1000006; struct Edge { int v; Edge *nxt; Edge(const int _v, Edge *h) : v(_v), nxt(h) {} }; Edge *hd[maxn]; int n, m, k, vistime, top, scnt; int MU[maxn], dfn[maxn], low[maxn], stack[maxn], belong[maxn], minv[maxn]; bool instack[maxn], haveind[maxn]; void tarjan(const int u); int main() { freopen("zay.in", "r", stdin); freopen("zay.out", "w", stdout); qr(n); qr(m); qr(k); MU[0] = 2333; for (int i = 1; i <= n; ++i) qr(MU[i]); for (int i = 1, u, v; i <= m; ++i) { u = v = 0; qr(u); qr(v); hd[u] = new Edge(v, hd[u]); } for (int i = 1; i <= n; ++i) if (!dfn[i]) { tarjan(i); } for (int u = 1; u <= n; ++u) { for (auto e = hd[u]; e; e = e->nxt) if (belong[u] != belong[e->v]) { haveind[belong[e->v]] = true; } } for (int i = 1; i <= scnt; ++i) if (!haveind[i]) { MU[minv[i]] = 0; } std::nth_element(MU + 1, MU + 1 + k, MU + 1 + n, std::greater<int>()); int ans = 0; for (int i = 1; i <= k; ++i) { ans += MU[i]; } printf("%d\n", ans); return 0; } void tarjan(const int u) { dfn[u] = low[u] = ++vistime; instack[stack[++top] = u] = true; for (auto e = hd[u]; e; e = e->nxt) { int v = e->v; if (!dfn[v]) { tarjan(v); low[u] = std::min(low[u], low[v]); } else if (instack[v]) { low[u] = std::min(low[u], dfn[v]); } } if (dfn[u] == low[u]) { int v, &_mv = minv[++scnt]; do { instack[v = stack[top--]] = false; belong[v] = scnt; if (MU[v] < MU[_mv]) _mv = v; } while (v != u); } }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号