2019.6.18 校内测试 分析+题解
话说校内怎么又考试了QwQ,哎考就考吧(随鸡硬便啦)
考试的三个题分别都再洛谷上:
P1067 多项式输出 传送门
P1068 分数线划定 传送门
P1069 细胞分裂 传送门
呜呜呜~T1之前在洛谷上刚做了,当时就记得有好多坑来着,没想到这次重蹈覆辙,哎,当时没及时将这个题整理下来,导致了我的印象不深刻,然后这个题就白丢了40分。
这就告诉我们要及时整理好博客啦,OK,考后我们都要整理博客的,走起:
T1 多项式输出

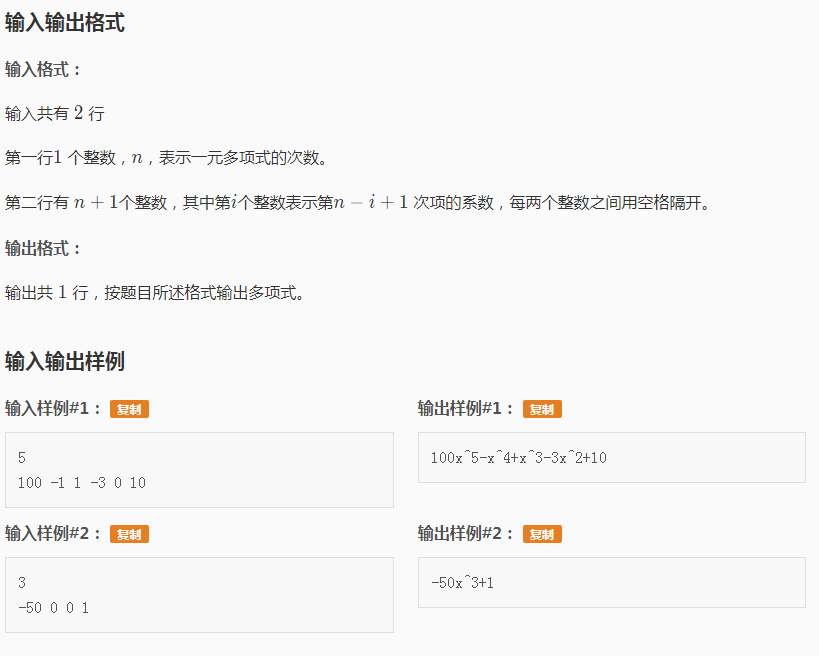

这个题真的是挺简单的,难度是普及-,只是有好多坑的地方,我对此做出了以下需要注意的地方(其实很多就是题目中强调的):
1.注意系数1和-1,我们不用输出那个数字,输出符合就好啦;
2.当x是1次方时,不需要输出"x^1";
3.最后的常数项若为0,不能输出是+0或-0,所以需要单独拿出来判断;
应该就上面这三个比较坑的地方了吧QwQ,尤其是第一条,我的第一项没有判断1和-1的情况,直接WA了4个点;
题外话说完了,下面上代码喽:
#include<iostream> #include<cstdio> using namespace std; int read() //读入优化 { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } int n,a[120]; //存每一项的系数 int main() { //freopen("poly.in","r",stdin); //freopen("poly.out","w",stdout); n=read(); for(int i=n;i>=0;i--) a[i]=read(); //每一项的系数,倒着存更方便哦 if(a[n]==1) cout<<"x^"<<n; //这里单独拿出来第一项的原因是解决符合的问题 else if(a[n]==-1) cout<<"-x^"<<n; //注意1和-1这两个特殊的系数 else cout<<a[n]<<"x^"<<n; */ //不是1或-1那么就正常输出 for(int i=n-1;i>=2;i--) { if(a[i]<0) { if(a[i]!=-1) cout<<a[i]<<"x^"<<i;//还是要注意-1的情况 else cout<<"-x^"<<i; } if(a[i]>0) { if(a[i]!=1) cout<<"+"<<a[i]<<"x^"<<i;//注意1的情况 else cout<<"+x^"<<i; } } if(a[1]>0) //单独处理倒数第二项 { if(a[1]==1) cout<<"+x"; //一再注意1 else cout<<"+"<<a[1]<<"x"; } if(a[1]<0) { if(a[1]==-1) cout<<"-x"; //二再注意-1 cout<<a[1]<<"x"; } if(a[0]>0) cout<<"+"<<a[0]; //单独处理最后一项 if(a[0]<0) cout<<a[0]; return 0; }
上面的T1毫无难度对不对,接下来看更简单的QwQ:
T2 分数线划定

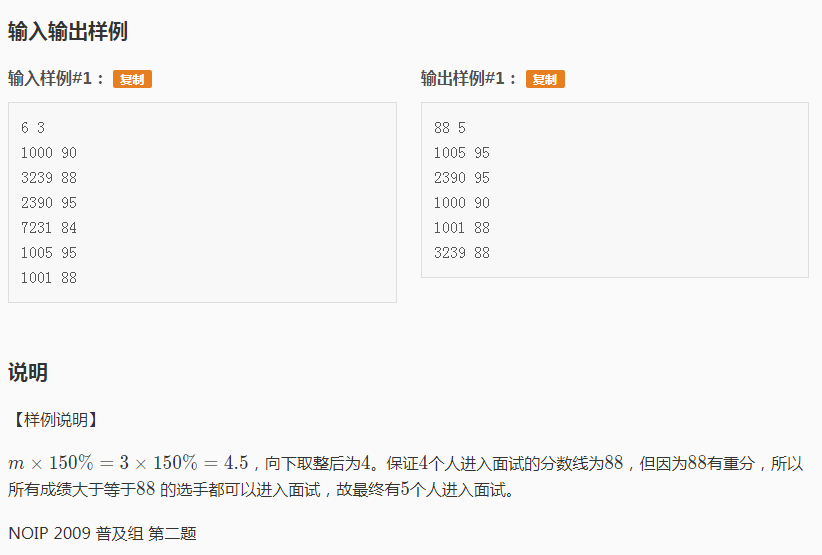
这个题也没什么好讲的,j竟然让我上去讲这个题,多么amazing的事,我就想问再看我博客的大佬们谁没有AC这道题?
咳咳,简单的说下思路吧:
1.输入n,m,然后我们就顺便把理想录取人数求出来,就设enter=(int)m*1.5,这里转个int就相当于向下取整了;其实我是不会告诉你我忘了是ceil还是floor了
2.按照分数排序,分数相同的编号小的靠前,这个写个自定义排序即可;
3.排完序后,我们直接找到第enter个人的分数,然后一直往后找,直到找到一个分数不同的,那么实际录取人数就是最后一个分数相同的人的下标;
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> using namespace std; int read() //读入优化 { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } int n,m,enter; struct people { int id,point; }a[5001]; int cmp(people x,people y) //按照分数大小排序 { if(x.point!=y.point) return x.point>y.point; else return x.id<y.id; //分数相同那么编号小的优先 } int main() { //freopen("score.in","r",stdin); //freopen("score.out","w",stdout); n=read();m=read(); enter=(int)(m*1.5); //理想进入面试的人数 for(int i=1;i<=n;i++) { a[i].id=read(); //编号 a[i].point=read(); //分数 } sort(a+1,a+1+n,cmp); //按照分数从大到小排序 int q=enter+1; //q为实际进入面试的人数 while(a[q].point==a[enter].point) q++; //一直找分数相同的 q--; //这里不要忘了减一,不懂得同学模拟一遍就好啦 cout<<a[q].point<<" "<<q<<endl; for(int i=1;i<=q;i++) printf("%d %d\n",a[i].id,a[i].point); //输出,好简单啊 return 0; }
T3 细胞分裂 -----小boss题


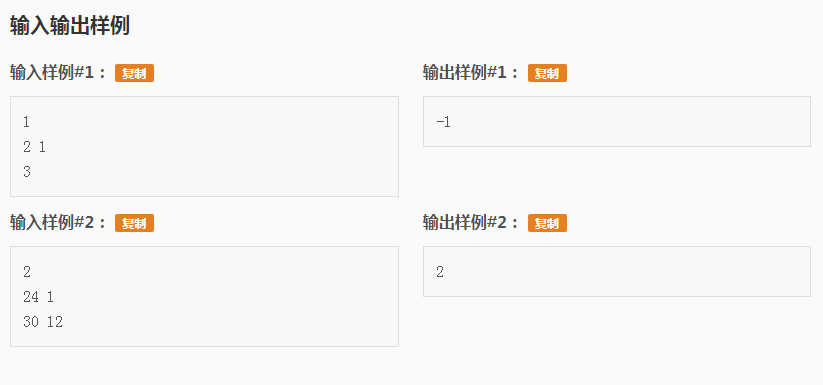

此题不会已放弃~~详情请见ych or ybr or wz 这些rank1的神仙们的博客吧!
算了,现在还是强行口胡一下我的思路吧:
我们看这个数据:m1的范围是30000以内,m2的范围是10000以内,若我们直接求m1^m2……,暴的不堪设想;
那么我们就要换一种别的方法喽,当然分解质因数可以,而且这个思路很好(详情出门转到ych的博客),但是我也说下我的思路啦:
首先我们将每种细胞单独拿出来考虑,就设它是Si 吧,那么总有m1^m2 | Si^n ,这里这个n就是要求的最小时间;
然后我们可以考虑求出来m1与Si的最大公约数gcdd,因为想到这个gcdd在前面会被算个gcdd^m2,在后面又会被算个gcdd^n,觉得有点浪费(当时我真的这么想),就单独将它摘出来吧;
有了最大公约数,我们就可以将m1^m2和Si^n转化一下形式啦:
设m1=m*gcdd,Si=s*gcdd,那么(m*gcdd)^m2 | (s*gcdd)^n,也就是 (m^m2)*(gcdd^m2)| (s^n)*(gcdd^n);
两边同除以(gcdd^m2)后得到: m^m2 | (s^n)*[ gcdd^(n-m2)];
我们继续看左边这个东东,它是不是很像原来我们一开始列出的式子:m1^m2 | Si^n 与 m^m2 | (s^n)*[ gcdd^(n-m2) ];
虽然只是有一点点像啦,但是这右边差的有点大啊qwq,能不能化简一下啦?
当然能!我们看一个定理:
若有两个互质的数p,q,则一定存在p^n mod q^m ≠ 0(其实是gcd(p^n,q^m)=1) ,其实就是无论多少次方都不能整除!
草草证明一下吧:
∵p,q互质,∴p和q无任何相同的因子
又∵p^n 和 q^m只是改变了因子的指数,而并没有增加或减少因子本身的数值
∴ 仍没有相同的因子,即仍互质
有了这个定理,我们就可以化简右边的一大堆式子了:
因为m和s是分别由m1和Si 同除以它们的最大公约数gcdd得到,那么m和s一定是互质的!(所有相同的因子都被除了,只剩下不相同的了)
那么也就是说,右边的s^n无论如何都不能使m^m2 | s^n,答案只可能从上面的gcdd^(n-m2)中产生!所以我们完全可以舍弃s^n来化简式子,那么式子就化简成:
m^m2 | gcdd^(n-m2) 我们可以将(n-m2)看成一个整体,这样就真的和我们一开始列出的式子很像了QwQ
所以我们还可以继续进行我们刚刚执行的操作:找最大公约数!
恩,继续找最大公约数:我们设gcddd=gcd(m,gcdd),则m=gcddd*_m,gcdd=gcddd*_gcdd (有点混,但是真的找不出来好变量名了,gcddd是最大公约数,_m是m除以最大公约数后剩下的数,_gcdd是gcdd除以最大公约数后剩下的数);
还是刚刚那样,用最大公约数将原先的m和gcdd表示出来:
m^m2 | gcdd^(n-m2)
=(gcddd*_m)^m2 | (gcddd*_gcdd)^(n-m2)
=gcddd^m2 * _m^m2 | gcddd^(n-m2)*_gcdd^(n-m2) 然后我们还是把最大公约数那一项除到右边来:
=_m^m2 | gcddd^(n-m2-m2)*_gcdd^(n-m2)
=_m^m2 | gcddd^(n-2 * m2)* _gcdd^(n-m2)
还是再套用上面的定理: ∵_m与_gcdd互质,那么我们可以舍弃_gcdd^(n-m2)
那么式子又简化为: _m^m2 | gcddd^(n-2 * m2)
然后我们还可以找最大公约数…………,有没有发现其实这就是一个递归操作,那有没有界限呢?
当然有!我们上述的操作其实就是一直将m1除以某个数,那么最后它一定会被除到1的!这样一来,式子就成了:
1^m2 | …………,对没错,1^m2还是1,那么这个问题就被我们巧妙的转化成了:
求最小的n,使得右边那一堆式子是整数!(是不是很神奇啊!)

我们来一组详细的数字来认真得体会上面的过程:
m1=96,m2=5
S1=36
那么我们先列出一个粗略的式子:
m1^m2 | S1^n(这个n和题目中的n不一样,这个n就是我们要求的最短时间),代入数据就是:96^5 | 36 ^n
首先求出gcd(96,36)=12,然后将最大公约数代入原式:
(12*8)^5 | (12*3)^n = (12^5)*(8^5)| (12^n)*(3^n),然后我们将最大公约数12那一项除到右边:
8^5 | 12^(n-5)*(3^n),运用定理可知3^n不可能产生答案,我们可以舍弃它:
8^5 | 12^(n-5),我们继续找到gcd(8,12)=4,并代入原式:
(4*2)^5 | (4*3)^(n-5)=4^5 * (2^5)| 4^(n-5)*[ 3^(n-5)],将最大公约数4的那一项除到右边:
2^5 | 4^(n-10)* [ 3^(n-5)],运用定理可知3^(n-5)不可能产生答案,我们可以舍弃它:
2^5 | 4^(n-10),我们继续找到gcd(2,4)=2,并代入原式:
(1*2)^5 | (2*2)^(n-10)=1^5 *(2^5)| 2^(n-10)* [ 2^(n-10)],你是不是已经知道了?把最大公约数2那一项除过去:
1^5 | 2^(n-15)*2^[(n-10)] = 1 | 2^(2n-25)
哇!我们将左边的m1给搞成1了耶,接下来的任务不就是求最小的n使得2^(2n-25)是整数了吗?
It is so easy! 列出不等式 2^(2n-25)>=2^0,则2n-25>=0,解得最小的整数n=13,(其实我们不用列不等式的,就是求出10和15的平均数再向上取整!)
so我们接下来总结一下我们每一步的操作,方便总结规律然后写代码:
1.求出m1和Si的最大公约数gcd;
2.若gcd=1,说明这两个数互质,则不可能有解,直接跳出;
3.将m1和Si用这个最大公约数表示出来,然后将左侧的最大公约数除到右侧去;
4.可以舍弃与左侧互质的部分,其实也就是Si / gcd 后的数;
5.从第一步开始继续重复上述操作,直到gcd=1或m1=1;
你会发现我们上述操作始终和m2没啥事,但是它不可能是来打酱油的吧QwQ~
其实它和最后的答案n有关,我们再来找一下m2的规律:
接下来这个例子我们不再将m2带进去了,这样能更好的找到规律哦:
m1=32, m2 ,S1=56
列出式子 m1^m2 | S1^n:
将m1,S1代入得: 32^m2 | 56^n;
第一大步操作:
1.求出gcd(32,56)=8;
2.gcd不为1,说明目前阶段有解;
3.原式=(8*4)^m2 | (8*7)^n ------用最大公约数表示
= 8^m2 *(4^m2)| 8^n*(7^n) ------拆括号
=4^m2 | 8^(n-m2)*(7^n) ------将最大公约数那一项除到右侧
4.舍弃与4^m2互质的那一项:7^n,原式成为:4^m2 | 8^(n-m2);
第二大步操作:
1.求出gcd(4,8)=4;
2.gcd不为1,说明目前阶段有解;
3.原式=(4*1)^m2 | (4*2)^(n-m2) ------用最大公约数表示
= 4^m2 *(1^m2)| 4^(n-m2)*[ 2^(n-m2)] ------拆括号
=1^m2 | 4^(n-m2-m2)*[2^(n-m2)] ------将最大公约数那一项除到右侧
=1 | 4^(n-2 * m2)*[ 2^(n-m2)]
4.左侧我们已经除到1了,那么我们就跳出,分析答案产生;
不知道各位在刚刚的例子中有没有发现有关m2的规律,来和我发现的规律对比一下哪个更好:
1.我们在第3步操作结束以后(就是将最大公约数那一项除过去后),右侧最大公约数的那一项的指数都会减去m2是吧,如果我们单独拿出来每一个大步(每一个循环)的话,我们可以发现:右侧最大公约数那一项的指数它减去的m2的个数是和当前这是第几大步是相同的(其实这个很好理解,我们每一个大步s的指数只减去1个m2,但是却非常重要);
我们可以来记录进入了几次循环来判断右侧最大公约数s那一项的指数减了几个m2,在代码中用 t 来记录;


2.同时它后面的q那一项的指数减去的m2的个数是t-1;
3.我们可以根据m2来求解最后的答案;
4.一个不是关于m2的规律(实在不知道要往哪放但是没有这个总结代码可能看不懂):
结合上面的例子,再感性理解一下,我们将左边的最大公约数除到右边后,左边只剩下了m1 / gcd,而右边呢?由于Si / gcd 后与m1 / gcd 互质,就被抛弃了QwQ~,所以右边只剩下了最大公约数gcd,So进行下一大步操作的就是 m1 / gcd | gcd(这里省略了指数方便理解) ,也就是说:我们令m1=m1 / gcd,Si = gcd 就可以进行下一大步操作了;
讲完了m2的规律后,我们就可以将上面的步骤转化成代码啦(其实很短):
m=m1; //拷贝一份m1的值 s=S[i]; //拷贝一份S[i]的值 flag=1; //判断是否有解 t=0; //记录最大公约数要减几个m2 while(m!=1) { gcdd=gcd(m,s); //第一小步,求最大公约数 if(gcdd==1) {flag=0;break;} //如果互质,那么肯定无解,直接跳出 m/=gcdd; //左边剩下了m/gcdd q=s/gcdd; //q就是s除以gcdd后剩下的数 s=gcdd; //舍弃q后,右边剩下了gcdd t++; //每进入一次循环,s的指数就要多减1个m2 }
下面就要动动脑筋仔细思考小细节了:
当然这个将m1除到1的过程是没有锅的吧,那么哪里还需要注意呢?
就是最后的求n的过程了!其实不知道小伙伴们有没有看出来我前面的例子中求n总是很含糊(因为还没讲到这里鸭),所以我就要帮帮带着疑惑看下来的小伙伴们仔细得考虑一下下:
假设我们已经分解到了最后一步,也就是m1已经被我们除到1了,那么右边的式子我们就可以写成:
s^(n - t * m2)*{ q^[ n - (t-1)*m2 ] } ------(这里s,q,t 的含义和上面代码中的含义相同,还有这里表示指数用了上面总结的公式,不懂得小伙伴可以再回到上面看看)
那么无非有这3种情况:
1. s 与 q 互质,也就是gcd(s,q)=1,这时候n=t * m2;
Why?因为这时候我们要保证右边那一坨式子最后算出来是个整数,而且这两个数还是互质的,所以若有一个是分数的话,另外一个数无论多少次方都不会把它乘成整数的qwq,所以我们要保证这两个数s和q的指数都要>=0,因为我们考虑到s的指数比q的指数多减了个m2,所以我们把s的指数搞成0的话,q的指数一定>0(显然这时候指数为m2),所以我们只考虑将s的指数弄成0就好啦,显然这时候n=t*m2;
2.gcdd是q的因数,也就是gcd(s,q)=gcdd,这时候n=ceil((t+(t-1)*tot)*m2 / (tot+1)),tot是q内含s的个数;
为什么还要把这种情况单独考虑呢?如果我们像第一种情况只考虑s的指数的话,直接n=t*m2 ?NO!因为既然q是s的倍数,那么必然我们将q进行分解质因数的话,里面会有s(但是指数不同),那么我们将s进行合并的话,指数不再是n-t*m2了,那是多少呢?------取决于q里面含有多少个s!
这是将q里面所有s全部分离出来的代码:
while(q%s==0) //如果q里面含有s,分离出来 { tot++; //tot表示能分离出来多少个s q/=s; }
为了区分,我们将分离出来的s叫做 _s,很显然 s 和 _s的指数不同是吧,那么我们考虑_s的指数是多少?
由于它是从q中分离出来的,那么显然_s 和q的指数是相同的,看到上面q的指数是[ n-(t-1)*m2 ],那么_s的指数也是[ n-(t-1)*m2 ];
那么我们是不是可以将s 和 _s合并起来鸭?(底数相同不就可以合并嘛?)
合并后的s的指数就是 [ n-(t*m2) ]+{ tot * [n-(t-1)*m2] } ,简单一记就是:1个s的指数+tot个_s的指数;
再想想哈~我们将q所有的 s都分解出来了,那么剩下的东东就和s互质了~ 所有这不就又变成了第一种情况了?
还是老样子,我们只要使得s的指数为0就是解了。
所以我们要解这个方程:[ n-(t*m2) ]+{ tot * [n-(t-1)*m2] } = 0
首先拆括号: n-t * m2 + { tot * [ n-(t * m2-m2)] }
=n- t * m2 + { tot * ( n - t * m2 + m2) }
=n - t * m2 + tot * n - t * m2 * tot + m2* tot
=0
我们将n放在左边,m2放在右边,于是我们得到:
n + tot * n = t *m2 +t *m2 *tot - m2 * tot
提取公因式: (1+tot)* n =m2 *(t + t * tot -tot)
(1+tot) * n = m2 * [ t + tot *(t -1) ]
最后我们将n的系数化1,就得到了答案:
n = m2 * [ t + tot *(t -1) ] /(1+tot) ------这过程觉得够详细了,我就不信lz还看不懂
So这种情况的n我们也搞定了(哎,有没有发现其实第一种情况就是tot=0的情况耶,我们完全可以将第一,二中情况合起来写)
代码如下:
while(q%s==0) //如果q里面含有s,分离出来 { tot++; //tot表示能分离出来多少个s,第一种情况就是tot=0的情况 q/=s; } if((t*m2+tot*(t-1)*m2)%(tot+1)==0) //我不知道为什么ceil出来的答案不对,只能自己模拟向上取整了 ans=(t*m2+tot*(t-1)*m2)/(tot+1); //没余数说明正好整除 else ans=(t*m2+tot*(t-1)*m2)/(tot+1)+1;//如果有余数就要+1(这个1就是余数除成小数后再向上取整后得到的) minx=min(minx,ans); //题目要求整体最小时间
3.gcd(s,q)≠1,gcdd ;这是什么意思呢?就是当s和q既不互质,也不是倍数关系的时候;
这种情况有什么魔力呢?你看如果我们用第二种情况的公式的话,显然tot=0(q不是s的倍数),但是我们注意到gcd(s,q)≠ 1,那么说明它们还有公共部分!
显然这个公共部分就是gcd(s,q),暂且记为 gc=gcd(s,q),所以我们要像第二种情况中的q分离s一样,分别将 s 和 q 中的 gc 分离出来(逃 ;
分离的过程和上面几乎一样:
while(q%gc==0) //如果q中含有gc就分离 { totq++; //q中含有gc的个数 q/=gc; } while(s%gc==0) //如果s中含有gc就分离 { tots++; //s中含有gc的个数 s/=gc; }
So我们就从s中分离出了 tots个gc,从q中分离出了 totq 个gc,当然这两部分 gc的指数是不同的;
其中 tots个gc的指数是和s的指数相同,均为 n - t * m2;totq 个gc 的指数是和q的指数相同,均为 n - (t -1)* m2 ;
然后我们将所有 gc 的指数合并(就是tots 个gc 和totq 个gc 的指数和):
tots *(n - t * m2)+totq * [ n -(t-1)* m2 ]
=tots * n - tots * t *m2 + totq * n - totq * m2 *(t-1)
我们已经把s 和 q的公共部分 gc全部都分离出来了,那么剩下的 (s / gc)和(q / gc)一定都与 gc 互质,这其实又转化成了第一种情况;
所以我们只需要将 gc 的指数搞成0 就好了:
令 gc 的指数为0:
tots * n - tots * t *m2 + totq * n - totq * m2 *(t-1)=0
tots * n + totq * n = tots * t * m2 + totq * m2 * (t-1) -----将有关m2的项移到右边
(tots + totq)* n= m2 * (tots * t + totq * (t-1)) ------提取公因式
n = m2 * (tots * t + totq * (t-1))/ (tots + totq) ------n系数化1
所以这种情况的公式我们也推出来了,所以这个题我们就做完了QwQ~
if((t*m2*tots+totq*(t-1)*m2)%(tots+totq)==0) //这种情况的公式,注意向上取整 ans=(t*m2*tots+totq*(t-1)*m2)/(tots+totq); else ans=(t*m2*tots+totq*(t-1)*m2)/(tots+totq)+1;
下面就是完整代码啦:
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> using namespace std; int read() //读入优化 { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } int n,m1,m2,minx,gcdd,m,s,q,t,flag,tot,ans,tots,totq; //t代表q能分解成多少个s int S[10001]; int gcd(int a,int b) //欧几里得算法求最大公约数 { if(b==0) return a; else return gcd(b,a%b); } int main() { n=read(); m1=read(); m2=read(); minx=1e9; if(m1==1) //这里一定要注意特判m1==1的情况,不然会TLE { cout<<0; //无需等待,因为任何数都是1的倍数 return 0; } for(int i=1;i<=n;i++) S[i]=read(); for(int i=1;i<=n;i++) { tot=0; m=m1; //拷贝一份m1的值 s=S[i]; //拷贝一份S[i]的值 flag=1; //判断是否有解 t=0; //记录最大公约数要减几个m2 while(m!=1) { gcdd=gcd(m,s); //第一小步,求最大公约数 if(gcdd==1) {flag=0;break;} //如果互质,那么肯定无解,直接跳出 m/=gcdd; //左边剩下了m/gcdd q=s/gcdd; //q就是s除以gcdd后剩下的数 s=gcdd; //将q舍弃后,右边只剩下了gcdd t++; //每进入一次循环,s的指数就要多减1个m2 } if(flag) { int gc=gcd(q,s); //先求出gcd(q,s) if(gc!=1&&gc!=s) //单独讨论第三种情况 { totq=0;tots=0; //注意清空 while(q%gc==0) //如果q中含有gc就分离 { totq++; //q中含有gc的个数 q/=gc; } while(s%gc==0) //如果s中含有gc就分离 { tots++; //s中含有gc的个数 s/=gc; } if((t*m2*tots+totq*(t-1)*m2)%(tots+totq)==0) //这种情况的公式,注意向上取整 ans=(t*m2*tots+totq*(t-1)*m2)/(tots+totq); else ans=(t*m2*tots+totq*(t-1)*m2)/(tots+totq)+1; minx=min(minx,ans); } else //第一,二种情况 { while(q%s==0) //如果q里面含有s,分离出来 { tot++; //tot表示能分离出来多少个s,第一种情况就是tot=0的情况 q/=s; } if((t*m2+tot*(t-1)*m2)%(tot+1)==0) //我不知道为什么ceil出来的答案不对,只能自己模拟向上取整了 ans=(t*m2+tot*(t-1)*m2)/(tot+1); //没余数说明正好整除 else ans=(t*m2+tot*(t-1)*m2)/(tot+1)+1;//如果有余数就要+1(这个1就是余数除成小数后再向上取整后得到的) minx=min(minx,ans); //题目要求整体最小时间 } } } if(minx==1e9) cout<<-1; //如果minx没被更新,说明无解 else cout<<minx; return 0; }
这种思路我也不知道是不是正解QwQ,如果有误请指出,我会认真完善的~
觉得这个思路比较不错的就点个推荐呗~~~
感谢你的观看QwQ~


