2019.6.12 校内测试 分析+题解
本着友谊赛的原则,校内又测试了一遍qwq,然而这次的题好难。
我就想问这句话是谁打的拖出去打死:
![]()
我个人认为最难的题应该是T1,其次T3,最后T2(T1思路挺好想,但我当时实现起来超麻烦,搞得我都放弃了,还好骗了40分);然后T2应该是道入门题吧,看了一下初三rank1神仙的代码,简直不能再短,不过这个题比的又不是代码,因为几乎都在10min~20min写出来了;最后就来到了T3求最短路的题,这个是真的无语,看着4个算法就是不知道用哪个,当时觉得应该用Floyd算法,因为有q次询问,然后就在那怼了一个小时也没怼出来,也没骗着分,悲剧爆零。
但是还是那句话,这只是一次小小的校内测试,还没真的到了NOIP赛场,现在查缺补漏还来得及,现在整理好博客,总结经验,一定会有所提升的,恩没错qwq!
好了,下面进入正题。
………………………………………………………………分割线………………………………………………………………………
T1 单词序列
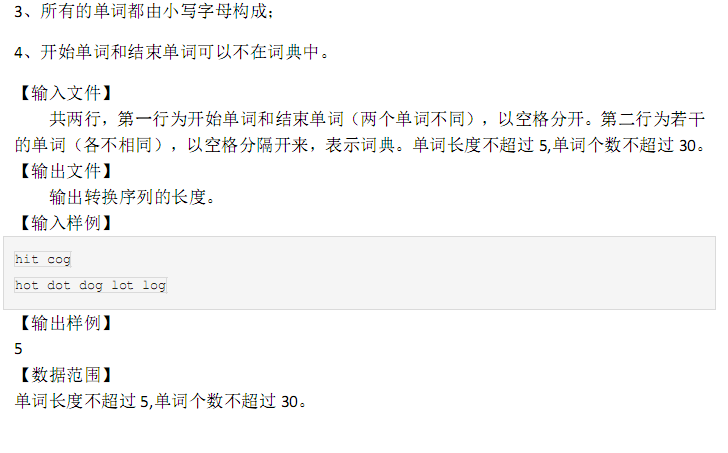
直接说正解:
这里我们用BFS,搜索序列长度为2,3,4……的序列的末尾单词的所有可能,如果当前这个末尾单词与结束单词只有一个字母不相同(下面称作“差异为1”),那么直接返回长度+1就行了,注意每个单词只能被遍历到一次,所以用vis数组记录下来,若每个单词都被遍历了还未搜到和结束单词相差1的单词,返回0(无解)。
样例图解:

第一步:

第二步:


第三步:


第四步:


第五步:


第六步:

将上面的步骤写成代码就是这样子滴:
int bfs(){ memset(vis,0,sizeof(vis)); q.push((node){ss,1}); //将起点入队:开始单词是序列的第一个元素,此时序列长度为1 while(!q.empty()){ node cur=q.front();q.pop(); //取出队首元素将它进行改变 if(can(cur.s,st)) return cur.dep+1;//如果该队首元素和结束单词的差异为1,那就不必再往下搜了,直接返回tep+1 for(int i=0;i<n;i++) if(!vis[i]&&can(cur.s,s[i])){ //找没访问过且与之差异为1的单词 q.push((node){s[i],cur.dep+1}); //入队,以后对它进行改变 vis[i]=1; //标记为访问过 } } return 0; //队列为空还没有变换到结束单词,说明无解返回0 }
看了图解,我们再重新理解一遍刚刚的思路:
可以看到队列中的元素的tep值是依次增大的,换句话说其实就是枚举长度为2,3,4,……n的序列的末尾单词的所有可能,直到这个末尾单词可以一步变换到结束单词,这时候我们就返回这个序列的tep+1,否则就一直往下搜;如果队列为空还未搜到与结束单词差异为1的单词,返回0;
然后考虑怎么输入若干个字符串:
这个应该就很简单了,一个while循环判断输入是否为真,是就继续读,否就停止读入跳出while循环。
下面是完整代码:
//bfs关键是开始和结束单词可以不在词典中 #include<cstdio> #include<iostream> #include<queue> #include<cstring> using namespace std; struct node{ string s; int dep; //dep是以s为序列末尾时序列的长度 }; queue<node>q; string ss,st,s[31]; int vis[31]; int n=0; int can(string s,string t){ //这个函数是用来比较两个字符串的 if(s.size()!=t.size()) return 0; //长度不相同,则字符串一定不相同,返回false int c=0; //c用来统计不一样的字母的个数 for(int i=0;i<s.size();i++) if(s[i]!=t[i]) c++; return c==1; //看看是否只有一个字母不同 } int bfs(){ memset(vis,0,sizeof(vis)); q.push((node){ss,1}); //将起点入队:开始单词是序列的第一个元素,此时序列长度为1 while(!q.empty()){ node cur=q.front();q.pop(); //取出队首元素将它进行改变 if(can(cur.s,st)) return cur.dep+1;//如果该队首元素和结束单词的差异为1,那就不必再往下搜了,直接返回tep+1 for(int i=0;i<n;i++) if(!vis[i]&&can(cur.s,s[i])){ //找没访问过且与之差异为1的单词 q.push((node){s[i],cur.dep+1}); //入队,以后对它进行改变 vis[i]=1; //标记为访问过 } } return 0; //队列为空还没有变换到结束单词,说明无解返回0 } int main(){ //freopen("word.in","r",stdin); //freopen("word.out","w",stdout); cin>>ss>>st; //输入开始单词和结束单词 while(cin>>s[n++]); //输入若干个字典单词,n统计个数 cout<<bfs()<<endl; return 0; }
T2 子集

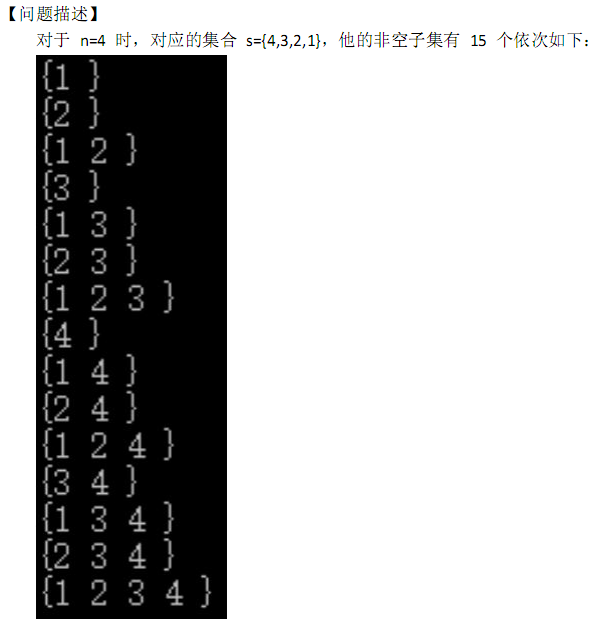

不得不说这个题是真的水,如果说T3是防AK的,那么T2就是防爆零的吧qwq。
题目中已经说的很明确了,编号是由集合里的元素状压一下然后转化成十进制后的数,那么我们已知编号m求集合元素,不就是相当于将编号转化成二进制来表示嘛?
由于数据小,我这里是暴力枚举2^20~2^0(不容易漏情况),m能减就减,记录下减的是几次方,最后输出次方+1(2^0的位置对应的是元素1,2^1的位置对应的是元素2,……);
#include<iostream> #include<cstdio> using namespace std; int two_pow[21],ans[21],n,m; int main() { //freopen("subset.in","r",stdin); //freopen("subset.out","w",stdout); cin>>n>>m; two_pow[0]=1; //2^0=1 for(int i=1;i<=20;i++) two_pow[i]=2*two_pow[i-1]; //预处理2^20以内 int k=20; while(m>0&&k>=0) { if(m-two_pow[k]>=0) ans[k]=1,m-=two_pow[k]; //m能减就减 k--; } for(int i=0;i<=20;i++) if(ans[i]==1) cout<<i+1<<" "; //别忘+1 return 0; }
T3 城市交通费

经过一番激烈的讨论,然后rqy又来解释了一波,我们终于明白了这个题QwQ。
值得肯定的是,考试的时候我的算法没错-----Floyd算法,也考虑到了再开一个数组存路径i---j所经过的最大城市的繁华度,但是,我没考虑到重边情况+繁华度排序!
接下来就给还未听懂的小伙伴们一步一步分析这个题,我会尽量让你们都懂的QwQ:
1.确定算法:
看到题目中说:有q组询问,每次询问从城市x到城市y所耗费的最小交通费。
虽然每一次小询问是问的单源最短路径,但是q次询问,尤其是当q特别大的时候,你如果要用求单源最短路的算法(Dijkstra,SPFA等),你需要算q次,显然TLE无疑;
而且回想起我们之前对付这个q次询问的办法:预处理!使得每次询问只用O(1)的时间就给出答案。
那么按照上面的思路,这个题就是先预处理出各个点到其他的最短路,明显的Floyd算法啦!
2.建图方式:
考虑到要用Floyd算法,那么一般就要用邻接矩阵来建图了,这个题n的范围:n<=250,邻接矩阵不会爆空间的。
建图的时候一定要注意一个小细节: 重边情况!
什么意思呢?就是说:输入数据十分的坑人,它可能会给你一个“1 2 3”来表示从城市1到城市2要花费3,然后下面的某一行可能会来个“2 1 5”来表示从城市2到城市1要花费5,显然从城市1到城市2就有两条路了,一条花费3,一条花费5;如果我们不注意的话,后输入的“2 1 5”会覆盖掉前面的“1 2 3”(邻接矩阵会这样,邻接表就不会了),所以在输入的时候我们需要比较一下原先a[i][j](初始化为无穷大)和输入的数据哪个小,我们取小的那个花费。
for(int i=1;i<=m;i++) { scanf("%d%d%d",&aj,&bj,&wj);//城市aj到城市bj需花费wj a[aj][bj]=min(a[aj][bj],wj);//若有重边,取最短的 a[bj][aj]=min(a[bj][aj],wj); }
3.Floyd算法的实现
这个题与以往Floyd模板不同的是:路径+最大繁华度 的总和最小才是最优解,所以我们单单的靠原来的模板会直接爆零(亲身试验qwq)。因为你光贪心的先用Floyd算出各个点到其他点的距离之后,再回过头来找路径中的最大繁华度的话,首先是时间复杂度受不了,其次难实现,最后正确性不高(三差做法)
其实这个题大家最困扰的地方就是城市的繁华度了,我们另外再开一个数组f[i][j],表示从城市i到j的最优解(路径+最大繁华度);
考虑初始化:
仔细的想想,刚开始输入完数据后,城市i到j是不是只有一条边直接连通?那么此时经过的城市是不是只有i和j?最大繁华度是不是只能由i和j产生?
所以我们就得到了f[i][j]=a[i][j]+max(p[i],p[j]) --------p[i],p[j]表示城市i,城市j的繁华度;
那么Floyd中我们每次都维护一下a[i][j]和f[i][j],到最后f[i][j]就是我们想要的最优解了。
又回到刚刚的问题:怎么求所经过城市的最大繁华度?
我们希望能找到一个城市k,使得k的繁华度是在所经过城市中是最大的。但是我们不能挨个找这个k,那咋办呢?
我们可以指定一个k,使得k的繁华度p[k]是从i到j所经过的所有城市中最大的,其他城市的繁华度都比p[k]小;
Q:为什么要这么实现?
A:这样最大繁华度只会在p[i],p[j],p[k]中产生;
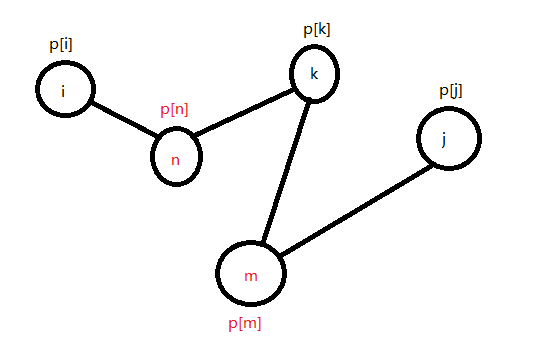
例如上图:假设我们已经使得k是从i到j所经过的城市中(n,k,m)繁华度最大的,由于我们要考虑加上最大繁华度,那么我们就不用再考虑n和m了,他们的繁华度都比k的小;
Q:指定听起来好高大尚啊!这个要怎么实现?
A:由于Floyd的中间点的枚举是在最外层(就是k的那层),这就使得我们在经过第k个城市的时候只会经过第1~k-1个城市(k是从小到大循环的,所以只能被小的k所更新);然后我们将k的意义改一下:我们不再按照城市编号来枚举了,我们按照繁华度从小到大来枚举==>那么就成为“我们在经过第k小繁华度的城市的时候只会经过第1~k-1小繁华度的城市”,那么此时我们枚举的这个中间点就是在经过的所有城市中繁华度最大的那个QwQ,所以我们只需要将所有城市的繁华度从小到大排个序就好啦。
到这里就可以上代码了,注释里面有详细的解释:
1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #include<queue> 5 #include<algorithm> 6 using namespace std; 7 int n,m,q,p[300],aj,bj,wj,x,y,f[300][300],a[300][300],top,t[300]; //a[i][j]表示城市i到j的最短路,f[i][j]表示城市i到城市j的最小交通费(路程+最大繁华度) 8 int cmp(int x,int y) //将城市按照繁华度进行排序 9 { 10 return p[x]<p[y]; 11 } 12 int main() 13 { 14 freopen("road.in","r",stdin); 15 freopen("road.out","w",stdout); 16 memset(a,0x3f,sizeof(a)); //将a数组初始化为无穷大 17 scanf("%d%d%d",&n,&m,&q); //n个城市,m条边,q次询问 18 for(int i=1;i<=n;i++) 19 scanf("%d",&p[i]); //每个城市的繁华度 20 for(int i=1;i<=m;i++) 21 { 22 scanf("%d%d%d",&aj,&bj,&wj); //aj到bj的路径为wj 23 a[aj][bj]=min(a[aj][bj],wj); //如果有重边,我们取较短的那条 24 a[bj][aj]=min(a[bj][aj],wj); 25 } 26 for(int i=1;i<=n;i++) 27 { 28 a[i][i]=0; //自己到自己的距离为0 29 t[i]=i; //第i个城市的编号是i 30 } 31 sort(t+1,t+1+n,cmp); //以p为关键字对t排序 32 for(int i=1;i<=n;i++) 33 for(int j=1;j<=n;j++) 34 f[i][j]=a[i][j]+max(p[i],p[j]); //一开始i到j直接连通,那么最大繁华度只可能在i和j中产生 35 for(int k=1;k<=n;k++) //Floyd算法,按照繁华度从小到大枚举中间点 36 for(int i=1;i<=n;i++) 37 for(int j=1;j<=n;j++) 38 { 39 a[i][j]=min(a[i][j],a[i][t[k]]+a[t[k]][j]); //更新最短路,t[k]是第k大的城市的编号 40 f[i][j]=min(f[i][j],a[i][j]+max(p[i],max(p[j],p[t[k]]))); //更新答案数组 41 /* 42 解释一下第40行为什么可以摆脱第39行而单独存在(就是即使不走t[k]也可以执行一遍第40行而不出错): 43 f[i][j]的初始化是:f[i][j]=a[i][j]+max(p[i],p[j]); 44 如果p[t[k]]的值比p[i]和p[j]都小,那么最大值就是max(p[i],p[j]),那么再加上a[i][j]可以发现和初始化一毛一样,所以f[i][j]不变; 45 如果p[t[k]]的值比p[i]和p[j]都大,那么最大值就是p[t[k]],显然再加上a[i][j]后比初始化都大,那么取个最小值f[i][j]还是没变; 46 所以就是:如果你不动a[i][j],f[i][j]打死都不变QwQ 47 所以就是你如果不执行第39行,第40相当于啥都没干;如果你执行了39行,第40行才有可能干点事 48 所以你完全可以把第39行改成if,把第40行放进if的大括号里,这样还减少时间复杂度 49 50 ----以上的证明是一个名叫gc并且每次都rank1的大佬的证的%%% 51 */ 52 } 53 for(int i=1;i<=q;i++) //q次询问 54 { 55 scanf("%d%d",&x,&y); 56 printf("%d\n",f[x][y]); //给出答案 57 } 58 return 0; 59 }
终于写完了QwQ~~




