2019.6.10 校内测试 分析+题解
2017 NOIP 模拟赛
T1 FBI树 传送门
T2 医院设置 传送门
T3 加分二叉树 传送门
我个人感觉T3挺难的(肯定是因为太弱了,前序遍历和中序遍历都不知道),T1和T2还好,至少在洛谷上AC了,不知道评测机咋了我T2爆零(哭 ;
哎,毕竟是一次小测试是吧,还好不是真正的NOIP,提前找到自己的不足,在此写博客记录此次的收获!
P1087 FBI树

这一道题挺简单的,手动模拟一下就好了,我们对样例进行模拟:
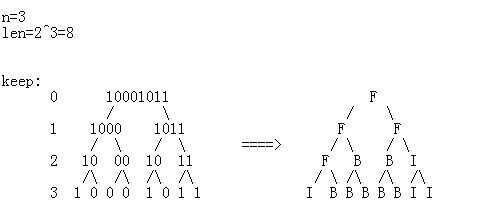
我们发现:输入的字符串会在第n层分解成为2^n个单独的字符;
我们可以反过来看:根结点所得到的字符串就是它的两个儿子结点拼起来的!
为什么这么看呢?因为我们知道根节点是F型的,将它拆分需要扫一遍才知道它的左右儿子是什么型的;但是我们已经知道叶子结点一定是B型或I型了,这样我们一层一层推上去就好了;
很显然有下面五种运算:
1.B+B=B;
2.I+I=I;
3.B+I=F;
4.B+F=F;
5.I+F=F;
贴一下后序遍历:
后序遍历(LRD)是二叉树遍历的一种,也叫做后根遍历、后序周游,可记做左右根。后序遍历有递归算法和非递归算法两种。在二叉树中,先左后右再根,即首先遍历左子树,然后遍历右子树,最后访问根结点。
然后就是我的代码啦:
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> using namespace std; int read() //读入优化 { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } int n; char ans[21000],m; //ans数组存储每个结点是什么型的 bool vis[21000]; //后序遍历要用到 int l[12000],r[12000]; //左右儿子的编号 void dfs(int now) //后序遍历输出 { if(l[now]==0||vis[now*2]==1&&vis[now*2+1]==1) //如果该结点没有儿子(叶结点)或儿子都已经遍历过了,就可以输出它了 { printf("%c",ans[now]); vis[now]=1; return ; } if(l[now]!=0&&vis[now*2]==0) dfs(now*2); //如果有左儿子却未遍历过,先找左儿子 if(r[now]!=0&&vis[now*2+1]==0) dfs(now*2+1); //如果有右儿子却未遍历过,再找右儿子 printf("%c",ans[now]); //最后再输出自己 return ; } int main() { //freopen("fbi.in","r",stdin); //freopen("fbi.out","w",stdout); scanf("%d",&n); int len=pow(2,n); //求出这个字符串的长度 for(int i=len;i<2*len;i++) //这里我们将每个单个字符摘了下来,从下标为2^n开始存 { cin>>m; if(m=='1') ans[i]='I'; //判断类型 if(m=='0') ans[i]='B'; } for(int k=n;k>=0;k--) //枚举层数,倒着往上推 { for(int i=pow(2,k);i<pow(2,k+1);i+=2) //枚举每一层的结点 { if(ans[i]=='I'&&ans[i+1]=='I') ans[i/2]='I'; //和为I型的情况 if(ans[i]=='B'&&ans[i+1]=='B') ans[i/2]='B'; //和为B型的情况 if(ans[i]=='B'&&ans[i+1]=='I'||ans[i]=='I'&&ans[i+1]=='B'||ans[i]=='F'||ans[i+1]=='F') ans[i/2]='F'; //和为F型的情况 } } //到这里我们就将这棵树建立起来了,接下来就是后序遍历了 for(int i=1;i<len*2;i++) //初始化 { l[i]=0; r[i]=0; vis[i]=0; } for(int i=1;i<len;i++) //记录0~n-1层每个结点的儿子 { l[i]=i*2; r[i]=i*2+1; } dfs(1); //从根结点开始找 return 0; }
这是wz大佬(并列rank1的神仙)的代码%%%:
#include <iostream> #include <string> using namespace std; int n; string s; char dfs(int l, int r) { if (l == r) { if (s[l] == '0') { cout << 'B'; return 'B'; } else if (s[l] == '1') { cout << 'I'; return 'I'; } } int mid = (l + r) / 2; char le = dfs(l, mid); char ri = dfs(mid + 1, r); if (le == 'B' && ri == 'B') { cout << 'B'; return 'B'; } if (le == 'I' && ri == 'I') { cout << 'I'; return 'I'; } cout << 'F'; return 'F'; } int main() { //freopen("fbi.in", "r", stdin); //freopen("fbi.out", "w", stdout); cin >> n >> s; dfs(0, (1 << n) - 1); cout << endl; }
P1364 医院设置

这道题貌似用Floyed,但是我怎么跟别人这么不一样,我是暴力枚举每个点作为医院,然后再求出最小值的(难道这就是我这个题爆零的原因?);
但是洛谷上AC了,说明算法还是没问题的qwq。
说下我的思路:
由于这个题每个点都可能作为根结点,所以我在存边的时候不仅要记录当前结点的儿子有谁,还要记录那个儿子的父亲是当前结点,目的就是让这两个结点联通(就是无论访问哪个点都能找到另一个点:儿子找父亲,父亲找儿子);
然后我们枚举每一个点作为根结点,模拟一遍:从当前点出发,同时用一个k来表示走了多少条边,我们可以按照“父亲---左儿子---右儿子”的顺序依次走,每走一层k++,用vis数组来存当前结点是否走过,ans+=k*当前结点的人数,最后再讲ans取个最小值就是答案了qwq:
代码如下:
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<cstring> using namespace std; int read() { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } struct city { int poeple,lc,rc,father; }a[101]; int n,vis[101],ans=0,minx; void search(int x,int k) //k是已经走过的边数 { if(a[x].father!=0&&vis[a[x].father]==0) //有父亲且没走过,那就先走父亲 { ans+=a[a[x].father].poeple*k; vis[a[x].father]=1; search(a[x].father,k+1); //从父亲接着往下走 } if(a[x].lc!=0&&vis[a[x].lc]==0) //走左儿子 { ans+=a[a[x].lc].poeple*k; vis[a[x].lc]=1; search(a[x].lc,k+1); } if(a[x].rc!=0&&vis[a[x].rc]==0) //走右儿子 { ans+=a[a[x].rc].poeple*k; vis[a[x].rc]=1; search(a[x].rc,k+1); } return ; //返回 } int main() { //freopen("hospital.in","r",stdin); //freopen("hospital.out","w",stdout); minx=1e8; //将minx初始化成一个很大的值 n=read(); for(int i=1;i<=n;i++) a[i].father=0; //初始化每个结点都没有父亲 for(int i=1;i<=n;i++) { a[i].poeple=read(); a[i].lc=read(); a[i].rc=read(); if(a[i].lc) a[a[i].lc].father=i; //记录儿子的父亲是当前结点 if(a[i].rc) a[a[i].rc].father=i; } for(int i=1;i<=n;i++) //枚举每个结点作为根结点 { memset(vis,0,sizeof(vis)); //注意清空 ans=0; vis[i]=1; search(i,1); //从根结点开始走 minx=min(minx,ans); } cout<<minx; return 0; }
然后是Floyed算法的代码(好像挺好理解的,还挺简单qwq):
#include<iostream> #include<cstring> using namespace std; const int inf=100000007; int p[101],dis[101][101],sum; int n,lch,rch; int main() { freopen("hospital.in","r",stdin); freopen("hospital.out","w",stdout); cin>>n; memset(dis,inf,sizeof(dis)); for(int i=1;i<=n;i++) { dis[i][i]=0; //自己到自己的距离为0 cin>>p[i]; cin>>lch>>rch; if(lch>=0) dis[i][lch]=1;dis[lch][i]=1; //建双向图 if(rch>=0) dis[i][rch]=1;dis[rch][i]=1; } for(int k=1;k<=n;k++) //Floyed算法求出任意两点间的线段数 { for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { if(dis[i][j]>dis[i][k]+dis[k][j]) dis[i][j]=dis[i][k]+dis[k][j]; } } } int minn=inf; for(int i=1;i<=n;i++) //枚举每个点作为根结点 { sum=0; for(int j=1;j<=n;j++) { sum+=p[j]*dis[i][j]; } if(minn>sum) minn=sum; } cout<<minn<<endl; return 0; }
这是wz大佬DP做法%%%tql :
#include <iostream> #include <queue> #include <cstring> #include <limits.h> using namespace std; int n; int lch[101], rch[101], fa[101], sum[101]; int dis[101][101]; bool vis[101]; int root; int main() { freopen("hospital.in", "r", stdin); freopen("hospital.out", "w", stdout); cin >> n; for (int i = 1; i <= n; i++) { cin >> sum[i] >> lch[i] >> rch[i]; fa[lch[i]] = fa[rch[i]] = i; } for (int i = 1; i <= n; i++) { root = i; } for (int i = 1; i <= n; i++) { queue<int> q; q.push(i); memset(vis, 0, sizeof(vis)); vis[i] = 1; dis[i][i] = 0; while (!q.empty()) { int node = q.front(); q.pop(); if (lch[node] && !vis[lch[node]]) { q.push(lch[node]); vis[lch[node]] = 1; dis[i][lch[node]] = dis[i][node] + 1; } if (rch[node] && !vis[rch[node]]) { q.push(rch[node]); vis[rch[node]] = 1; dis[i][rch[node]] = dis[i][node] + 1; } if (fa[node] && !vis[fa[node]]) { q.push(fa[node]); vis[fa[node]] = 1; dis[i][fa[node]] = dis[i][node] + 1; } } } int ans, ansv = INT_MAX; for (int i = 1; i <= n; i++) { int nowans = 0; for (int j = 1; j <= n; j++) { nowans += dis[i][j] * sum[j]; } if (nowans < ansv) { ansv = nowans; ans = i; } } cout << ansv << endl; }
P1040 加分二叉树

注:
前序遍历(DLR),是二叉树遍历的一种,也叫做先根遍历、先序遍历、前序周游,可记做根左右。前序遍历首先访问根结点然后遍历左子树,最后遍历右子树。
中序遍历(LDR),是二叉树遍历的一种,也叫做中根遍历、中序周游。在二叉树中,中序遍历首先遍历左子树,然后访问根结点,最后遍历右子树。
题目要求说求一棵符合中序遍历为(1,2,3,…,n)且加分最高的二叉树tree。也就是说这棵树的根结点左边都是左子树,右边都是右子树。

若3是根结点,那么它的左边的结点都在它的左子树里,右边的结点都在它的右子树里(因为中序遍历是按照“左---根---右”输出的);
所以我们只要记录好一个区间的根,就可以知道它的左子树和右子树了,这也方便了我们以后的前序遍历,我们就用root[i][j]来表示区间[i,j]这些结点中的根结点是谁;
然后我们可以用区间DP来解决这个题:
用数组f[i][j]来表示在区间[i,j]内的最大加分,这样考虑的话最后的答案一定是f[1][n]了。然后按照区间DP的套路,我们要枚举区间长度和区间位置:
for(int i=1;i<n;i++) //枚举区间长度 for(int j=1;i+j<=n;j++)//枚举区间位置,这里j是区间左端点的位置
有了区间长度i和左端点位置j,那么右端点位置显然是t=i+j ;然后我们求这个区间的最大加分,我们先以这个区间的左端点为根的最大加分算出来,然后依次枚举j+1~t分别作为根所求出的最大加分,看看是否大于以左端点为根的最大加分,大于就将它替换,同时将root[j][t]赋值为最大加分更大的所对应的那个根:
for(int i=1;i<n;i++) //枚举区间长度 { for(int j=1;i+j<=n;j++)//枚举区间位置,这里j是区间左端点的位置 { int t=i+j; //区间右端点 f[j][t]=f[j][j]+f[j+1][t]; //先以左端点为根 root[j][t]=j; //更新区间[j,t]的根为左端点j for(int k=j+1;k<=t;k++) //枚举区间内其他的点作为根结点 { if(f[j][t]<f[j][k-1]*f[k+1][t]+f[k][k]) //如果发现了更大的加分就更新这个最大加分 { f[j][t]=f[j][k-1]*f[k+1][t]+f[k][k]; root[j][t]=k; //同时将区间[j,t]的根结点更新为k } } } }
然后解决最后一道难关:前序遍历!!
因为前序遍历是按照“根---左---右”的顺序遍历的
所以我们先输出整棵树[1,n]的根结点root[1,n],然后分别再输出左子树和右子树,而左子树和右子树也要前序遍历按照“根---左---右”的顺序遍历,那就先输出左子树的根,再将左子树细分成小左子树和小右子树(暂时先这么叫吧),……循环往复,一直到了叶结点没有子树了就返回。所以前序遍历我们就用递归做:
void qx(int l,int r) //前序遍历:根---左---右 { if(l>r) return ; //如果不合法直接返回 printf("%d ",root[l][r]); //先输出根结点 if(l==r) return ; //如果就一个点那就返回 qx(l,root[l][r]-1); //然后输出左子树 qx(root[l][r]+1,r); //最后输出右子树 }
完整代码如下:
#include<iostream> #include<cstdio> using namespace std; int n,f[31][31],root[31][31],a[31]; //dp[i][j]存储区间[i,j]的最大加分,root[i][j]存储区间[i,j]的根结点编号 void qx(int l,int r) //前序遍历:根---左---右 { if(l>r) return ; //如果不合法直接返回 printf("%d ",root[l][r]); //先输出根结点 if(l==r) return ; //如果就一个点那就返回 qx(l,root[l][r]-1); //然后输出左子树 qx(root[l][r]+1,r); //最后输出右子树 } int main() { cin>>n; for(int i=1;i<=n;i++) { cin>>a[i]; } for(int i=1;i<=n;i++) { f[i][i]=a[i]; //一开始区间[i,i]也就是点i,值就是a[i] root[i][i]=i; //区间[i,i]的根肯定是i,因为就它一个元素 } for(int i=1;i<n;i++) //枚举区间长度 { for(int j=1;i+j<=n;j++)//枚举区间位置,这里j是区间左端点的位置 { int t=i+j; //区间右端点 f[j][t]=f[j][j]+f[j+1][t]; //先以左端点为根 root[j][t]=j; //更新区间[j,t]的根为左端点j for(int k=j+1;k<=t;k++) //枚举区间内其他的点作为根结点 { if(f[j][t]<f[j][k-1]*f[k+1][t]+f[k][k]) //如果发现了更大的加分就更新这个最大加分 { f[j][t]=f[j][k-1]*f[k+1][t]+f[k][k]; root[j][t]=k; //同时将区间[j,t]的根结点更新为k } } } } cout<<f[1][n]<<endl; //此时的f[1][n]就是区间[1,n]也就是整棵树的最大加分 qx(1,n); //前序遍历 return 0; }


