T2695 桶哥的问题——吃桶 题解
校内测试 ------T3


思路分析:
这个题要你求所有套餐的总价值,先看一眼产生套餐的条件:
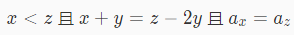
让我们对 $x + y = z - 2y$ 这个式子进行化简:
$x + y = z - 2y$ $=>$ $ x + 3y = z$ $=>$ $ z - x=3y$
产生的价值为:
$(x+z)*(b_x-b_z)$
我们可以注意到 $y$ 对产生的价值的贡献为 $0$(就是说跟 $y$ 没什么关系),所以上面的式子其实我们知不知道 $y$ 也就无所谓了,知道了也没什么用,还不如不知道$qwq$。
化简之后,我们可以重新来定义一下产生套餐的条件了:
$x<z$ 且 $(z-x)%3=0$ 且 $a_x=a_z$
所以暴力的同学就不用开三重循环啦,两重就够了。
之前的悲惨代码,跑得超慢,差不多$7s$:
#include<iostream> #include<cstdio> using namespace std; int read() { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } int n,m,ans; const int mod=10007; int a[100001],b[100001]; int main() { n=read();m=read(); for(int i=1;i<=n;i++) b[i]=read()%mod; for(int i=1;i<=n;i++) a[i]=read(); for(int x=1;x<=n;x++) { for(int z=x;z<=n;z+=3) { if(z==x) continue; if(a[z]==a[x]) ans+=(x+z)*(b[x]-b[z])%mod; } } cout<<(ans+mod)%mod; return 0; }
然后,$rqy$ 神仙讲了一个 $Θ(n)$ 的算法,直接从 $7223ms$ 降到了 $90ms$!
讲下 $rqy$ 的思路:
跟上面不同的是,我们套餐的价格不再是按照上面的公式求了,而是把它展开:
$(x+z)*(b_x-b_z)=xb_x-xb_z+zb_x-zb_z$
我们从 $1~n$ 枚举每一个 $z$,那么对于 $z$ 前面的所有下标相差 $3$ 的整数倍且与 $z$ 同种的 $x$ 都可以与 $z$ 产生一个套餐,那么 $ans$ 都要加一下上面的那个公式;
我们先假设我们枚举到的这个 $z$ 它的前面有 $3$ 个符合条件的 $x$,分别记为 $x_1,x_2,x_3$。
$x_1$ 与 $z$ 产生的套餐的价值为:$(x_1+z)*(b_{x_1}-b_z)=x_1b_{x_1}-x_1b_z+zb_{x_1}-zb_z$
$x_2$ 与 $z$ 产生的套餐的价值为:$(x_2+z)*(b_{x_2}-b_z)=x_2b_{x_2}-x_2b_z+zb_{x_2}-zb_z$
$x_3$ 与 $z$ 产生的套餐的价值为:$(x_3+z)*(b_{x_3}-b_z)=x_3b_{x_3}-x_3b_z+zb_{x_3}-zb_z$
那么对于当前这个 $z$,它能产生的价值就是:$(x_1b_{x_1}-x_1b_z+zb_{x_1}-zb_z)+(x_2b_{x_2}-x_2b_z+zb_{x_2}-zb_z)+(x_3b_{x_3}-x_3b_z+zb_{x_3}-zb_z)$;
我们将它进行合并同类项,得到:$(x_1b_{x_1}+x_2b{x_2}+x_3b_{x_3})-b_z(x_1+x_2+x_3)+z(b_{x_1}+b_{x_2}+b_{x_3})-zb_z*3$;
我们可以将这个式子进行推广,假设 $z$ 前面有 $n$ 的符合条件的 $x$,那么当前这个 $z$ 能产生的总价值就是:
$(x_1b_{x_1}+x_2b_{x_2}+x_3b_{x_3}+……+x_nb_{x_n})-b_z(x_1+x_2+x_3+……x_n)+z(b_{x_1}+b_{x_2}+b_{x_3}+……+b_{x_n})-zb_z*n$
$=\sum_{i=1}^{j}x_i*b_{x_i}-b_z*(\sum_{i=1}^{j}x_i)+z*(\sum_{i=1}^{j}b_{x_i})-zb_z*\sum_{i=1}^{j}1$
这个公式就是这个 $Θ(n)$ 算法的核心!
所以对于当前 $z$,我们只要求出它前面的 $\sum_{i=1}^{j}x_i*b_{x_i}$,$\sum_{i=1}^{j}x_i$,$\sum_{i=1}^{j}b_{x_i}$,$\sum_{i=1}^{j}1$,那么 $z$ 产生的总价值我们就可以 $Θ(1)$ 算出,再加上我们枚举的范围是$1~n$,所以这个算法的复杂度为 $Θ(n)$!
但是,怎么求那上面的那几个 $\sum_{i=1}^{j}$ 呢?
问得好!我们开数组来分别存上面的几个 $\sum_{i=1}^{j}$的值,注意这几个数组的下标都是种类:
$sx[i]$ 表示前面x下标的总和 $\sum_{i=1}^{j}x_i$
$sbx[i]$ 表示前面 $x$ 的美味值的总和 $\sum_{i=1}^{j}b_{x_i}$
$sxbx[i]$ 表示前面 $x$ 的下标乘美味值的总和 $\sum_{i=1}^{j}x_i*b_{x_i}$
$s[i]$ 表示前面 $x$ 的个数 $\sum_{i=1}^{j}1$
首先我们要解决 $x$ 和 $z$ 下标差 $3$ 的倍数的问题,这个好弄,将 $mod$ $3=0$ 的存为一类,$mod$ $3=1$ 的存为一类,$mod$ $3=2$ 的存为一类,那么对于每一类它们的下标相差一定是 $3$ 的倍数;
然后我们要解决 $x$ 和 $z$ 要属于同一种的问题,这就要用到了我们之前把数组的下标定位种类的原理了:
我们将每一种类的桶的 $\sum_{i=1}^{j}$ 都存在了数组里面,所以我们只要找和 $z$ 种类相同的就行了,$ans$ 更新如下:
ans=(ans+sxbx[a[z]])%mod; ans=(ans-z%mod*b[z]%mod*s[a[z]]%mod)%mod; //这里多mod几遍,可能会爆int ans=(ans+z*sbx[a[z]]%mod)%mod; ans=(ans-b[z]*sx[a[z]]%mod)%mod;
更新完 $ans$ 之后,对于以后的 $z$,当前的 $z$ 也有可能成为 $x$,所以我们要让 $z$ 更新一下和 $z$ 属于同一种的 $\sum_{i=1}^{j}$:
sxbx[a[z]]=(sxbx[a[z]]+z*b[z]%mod)%mod; s[a[z]]=(s[a[z]]+1)%mod; sbx[a[z]]=(sbx[a[z]]+b[z])%mod; sx[a[z]]=(sx[a[z]]+z)%mod;
到这里,就做完了,完整代码如下:
#include<iostream> #include<cstdio> #include<algorithm> #include<queue> #include<cstring> using namespace std; int a[100005],b[100005],sxbx[100005],sx[100005],sbx[100005],s[100005]; int read() { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } int n,m; long long ans; const int mod=10007; int main() { n=read(); m=read(); for(int i=1;i<=n;i++) b[i]=read()%mod; //种类a,美味值b for(int i=1;i<=n;i++) a[i]=read(); ans=0; for(int c=1;c<=3;c++) //一共三类:mod(3)=1 / 2 / 3 { memset(sxbx,0,sizeof(sxbx)); //千万不要忘了清零,防止对其他类的影响 memset(s,0,sizeof(s)); memset(sbx,0,sizeof(sbx)); memset(sx,0,sizeof(sx)); for(int z=c;z<=n;z+=3) //解决下标差3的倍数的问题 { ans=(ans+sxbx[a[z]])%mod; //更新ans值,注意要和z同种 ans=(ans-z%mod*b[z]%mod*s[a[z]]%mod)%mod; //这里多mod几遍,可能会爆int ans=(ans+z*sbx[a[z]]%mod)%mod; ans=(ans-b[z]*sx[a[z]]%mod)%mod; sxbx[a[z]]=(sxbx[a[z]]+z*b[z]%mod)%mod; //加上z的贡献,注意要和z同种 s[a[z]]=(s[a[z]]+1)%mod; sbx[a[z]]=(sbx[a[z]]+b[z])%mod; sx[a[z]]=(sx[a[z]]+z)%mod; } } cout<<(ans+mod)%mod; //防止答案为负数 return 0; }

