五一培训 清北学堂 DAY3
今天是钟皓曦老师的讲授~
今天的内容:动态规划

1.动态规划
动态规划很难总结出一套规律
例子:斐波那契数列 0,1,1,2,3,5,8,……
F[0]=0
F[1]=1
F[[n]=f[n-1]+f[n-2] n>=2
符合动态规划:
1.有边界条件:f[0]=0,f[1]=1,因为前两项不依赖任何斐波那契数列的值
2.有转移方程:F[[n]=f[n-1]+f[n-2] n>=2
3.有状态:f[0],f[1],f[2]……f[n-1],f[n],用已有的状态f[0]=0,f[1]=1来求出未知状态f[n]
贴一下zhx的笔记:

动态规划的无后效性与DAG有向无环图是一样的!
一种写动态规划的方法:记忆化搜索
另外还有两种方法:顺着推,倒着推(zhx起的名字qaq) (先不考虑矩阵加速qaq)
倒着推的代码:

一波带有注释的代码qaq(虽然你们都懂):
#include<cstdio> #include<iostream> using namespace std; int n,f[233]; //存每项斐波那契数列的值 int main() { cin>>n; //求第n项的斐波那契数 f[0]=0; //已经给出的条件 f[1]=1; //已经给出的条件 for(int a=2;a<=n;a++) f[a]=f[a-1]+f[a-2]; //利用公式求每一项的值 cout<<f[n]<<endl; }
顺着推的代码:

还是一波带有注释的代码:
#include<cstdio> #include<iostream> using namespace std; int n,f[233]; //存每项斐波那契数列的值 int main() { cin>>n; f[0]=0; //已经给出的条件 f[1]=1; //已经给出的条件 for (int a=0;a<n;a++) { f[a+1]+=f[a]; //对于每一个斐波那契数,它影响的只有它后面的两个 f[a+2]+=f[a]; //所以我们只有将它后面两个分别加上该项的值 } cout<<f[n]<<endl; //输出第n项 }
思路:我们知道f[a]已经算出来了,那么我们考虑f[a]会影响哪几项斐波那契数列的值?
显然是f[a+1]和f[a+2]这两项!让他们分别加上f[a]的值,更新一下
顺推和倒推的区别:一种是别人更新自己(倒着推),一种是自己更新别人(顺着推),都要掌握,有时候会有复杂度的区别
第三种写法——记忆化搜索:
先来一发普通搜索:

搜索求斐波那契数列!
复杂度是神奇的O(f[n]),因为是从1一个一个往上加出来的,一直加到f[n]
斐波那契数列的通项公式:

时间复杂度大概是0(1.6^n),太慢!!!不能接受!!!
所以我们用记忆化搜索!
代码慢的原因:有很多值被算了多次,但因为每个值算出来不变,所以算一次就好了
所以我们要保证每个值只被算一次,这就叫记忆化搜索!
我们开两个数组:
 记录第n项斐波那契数列有没有被算过!
记录第n项斐波那契数列有没有被算过!
 存斐波那契数列的值
存斐波那契数列的值
加上一步:
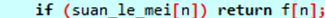
如果算过,直接返回值,不用再算
完整代码:

#include<iostream> #include<iostream> using namespace std; int f[10000],n; //f数组存斐波那契数列的值 bool suan_le_mei[10000];//suan_le_mei(算了没)数组存是否已经算过 int dfs(int n) { if (n==0) return 0; //如果搜到了已知条件,直接返回 if (n==1) return 1; //如果搜到了已知条件,直接返回 if (suan_le_mei[n]) return f[n]; //如果这一项已经算过了,直接返回 suan_le_mei[n]=true;//来到这里说明这一项没被算过,将它标记为算过 f[n]=dfs(n-1)+dfs(n-2); //将它算出来 return f[n]; //返回第n项的值 }// 时间复杂度O(n),因为每一项只被算了一次,共要算n项 int main() { cin>>n; cout<<dfs(n)<<endl; //神搜第n项的值 return 0; }
时间复杂度:O(n) 因为每一项只被算了一次!
因为记忆化搜索开了两个数组,所以空间变大
同样是空间换时间,然而矩阵优化的O(log n)的复杂度更优秀(快速幂的复杂度)
常见的动态规划种类:
1.数位DP (NOIP中出现率:5%)
2.树形DP (NOIP中出现率:5%)
3.状压DP (NOIP中出现率:5%)
4.区间DP (NOIP中出现率:5%)
5.其他DP (NOIP中出现率:80%)
Zhx:前四种DP有套路
OI中不会考的DP:插头DP,博弈论DP (完全没听过qaq)
1. 数位DP

举个例子:
读入两个正整数l,r,问从l到r有多少个数?
Ans: r-l+1
因为太没挑战性,所以我们尝试用数位DP来解决这个题qaq:
可以将问题转化为:[l,r]=[0,r]-[0,l-1](前缀和)
所以现在我们的问题就是求[0,x]有多少数!
先将x的十进制表示写出来:
X[n],x[n-1],x[n-2],……,x[0] 这里x[0]表示x的个位是多少,x[1]表示x的十位是多少……
我们看[0,x]中有多少个数,实际上就是找有多少个v满足0<=v<=x
因为x只有n位,所以v最多也有n位
v[n],v[n-1],v[n-2],……,v[0] v可以有前导0
所以问题就是往这几位上填一个0~9中的某一个,问有多少填充方案满足v<=x
那么怎么填呢?
数位DP是从高位到低位填的!
若我们已经填到了v[n-2],则v[n-1]和v[n]一定是已经填好了的!

假设我们填v[n-3],分两种情况讨论:


则v[n-3]可以填0~9的任何一位

则v[n-3]只能填:0~x[n-3]
定义状态:
F[i][j] 中i表示已经填到了第i位,j表示第i位的x[i]是大于v[i]还是等于,0是大于,1是等于,f[i][j]代表这种情况的方案数是多少。

状态转移方程?
枚举第i-1位填什么。
将x的每一位记录下来:

两遍solve记得情空数组:

我们填第n位时要从第n+1位转移过来,因为没有第n+1位,所以第n+1位都为0,那么我们就找到了边界条件。

初始化:第n+1位填相等的数的方案数有1种
开始枚举每一位:

分两种情况:相等或大于


如果b==0,说明前面填的位已经小于x了,那么v可以填0~9,并且填完之后还小于x
所以每填完一个数都要加上前面第a+1位时v小于x的方案数来作为第a位的方案数(虽然有点奇怪,但是便于理解qaq)

如果b==1,说明前面按的位等于x了,所以这时我们的v只能填0~z[a]的数来保证v小于等于x了,但又要细分两种情况:
- 当前填的v的这一位v[a]小于x的这一位x[a],则要把前面相等的方案数加到第a位不相等的方案数里,因为v的这一位已经填了一个比x的这一位小的数了,后面再怎么填也是v小于x;
- 当前填的v的这一位v[a]等于x的这一位x[a],则要把前面相等的方案数加到第a位的v等于x的方案数里
最后我们就直接输出大于和相等的方案数就好啦:



比上个题多一个条件,所以在上面个题多加一个维度就行了!
也就是说有几个条件就加几个维度表示几个状态;

填第i位时相邻的有第i+1和第i-1位,但又因为第i-1位还没填,所以没有影响
Zhx不写代码了qaq!让我们自己想想!
并抛给了我们一个洛谷蓝题:Windy 数
3.树形DP

画个树:

F[i]表示以i这个点为根的子树里有多少个点
只能确定叶子节点的f值为1

状态转移方程:

P1和P2分别是它的两个儿子结点

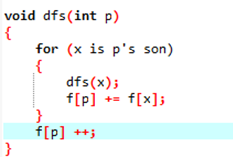
稍微写下代码:

从根节点开始往下找,所以是dfs(1);
一波超级伪的代码(无力吐槽):
For循环里的意思是x是p的儿子,相信各位都看得懂英语吧
Problem :
给出一个n个点的数,求这棵树的直径是多少:
所谓直径,就是结点中的最远距离

考虑一个问题,树上的路径长什么样?
最大路径一定是:先向上走到某个点,再向下走到一个你想要到的点。
因为这样走的话能走两端,总比你一段向下走要走的多!

因为求最大路径不涉及方向,所以我们可以将向上再向下看成从一个结点向它的其中两个儿子往下走!
所以就是要找从一个点向下走最长和次长能走多少,拼起来就是以这个结点作为经过这个拐点的最长路径。
怎么求呢?动态规划!
定义状态:

怎么转移状态?
求一个点的答案,就要把它所以儿子的答案整合在一起!

要决定到底要走到哪个儿子去!从它儿子中找个最大的,再从它往下走。
最长路状态转移方程:

我们分别找出当前P结点的每个儿子向下走的最大路径,贪心算法选择路径最大的那个往下走,这样一定是最优解!别忘了加一,是P与儿子间的路径。
次长路状态转移方程:

假设我们当前已经选择的那个最长路径的儿子结点为Pk,则在选择次长结点时不能再选择Pk了,因为如果再选择Pk的话,父亲结点P和儿子结点Pk之间的路径就会被走两次,这样是不合法的!所以我们只能从其他儿子结点的最长路(注意不是次长路)中找一个最大的,作为P的次长路!
最终答案: min(f[i][1]+f[i][0])
3. 区间DP
看个题:
有n堆石头,要将它们合并为一堆石头,每次合并的代价就是两堆石头的重量和,问怎么合并使代价最小?
状态:f[l][r]代表把第l堆石子到第r堆石子合并所花的代价
边界条件:f[i][i]=0 不用合并,代价为0
最后一次合并:某两堆石头合并
合并并不改变石头的顺序
所以我们一定会找到一个分界线,使得分界线左边的石头合并成一堆石头,将分界线右边的石头合并成一堆,然后最后合并成一堆

转移方程:

Sum表示从l到r的每个石子的重量和。
代码如下:

但是是错的,因为你用未算过的值来更新算过的值(我们已经让p=l了,所以p+1肯定大于l,这样就出现了一个问题:我们在算区间[l,r]的时候用到了[p,r]也就是[l+1,l],但这个for循环还没循环到l+1,所以区间[l+1,r]的值我们是不知道的!),所以答案肯定不对。
所以我们最外层改为枚举长度,换下写成就对了:

我们这次将区间的长度作为for循环的最外层,因为我们已经将f[a][a]都赋值为0了,也就是说,这些长度为1的区间已经被算过了,这样我们就可以去推长度为2的区间,因为我们枚举的分界线p可以将这个长度为2的区间分成两个长度为1的区间,这样就能得出长度为2的区间的值,当长度为3时,分界线p又可以将区间分成一个长度为1另一个长度为2的区间,这样一来就能保证用已经算过的值来推未知的值!
时间复杂度O(n^3)
4.状压DP


看个TSP问题(旅行商问题):
给一个平面内的若干点,求从一点走完所有点所走到路径最短是多少?
这个题不可能比O(2^n)更快!!!所以用最小生成树的方法不对!(因为最小生成树的复杂度是个多项式)
我们发现了一个贪心策略:最优情况下每个点只经过一次

状压即状态压缩,怎么进行状态压缩呢?
我们可以用一个二进制数来表示状态!
具体表示方法就是弄一个n位的二进制数,从右往左若第i位的值为1,说明选择了第i个点:
011001代表集合中有{1,4,5}

状态定义:用f[s][i]表示状态为s(一个n位的二进制数,表示集合内的数)且当前停留在i的最短路
转移过程就是不断是走过的点变多,也就是把s的二进制中将0不断的变成1,这样的话s会增大,所以我们以s为依据开始枚举,能保证状况不重复;
当s为1时,对应的二进制就是00000……1,这就代表了只选了起点并没有走;当s为2^n-1时,对应的二进制就是11111……1,这就代表了每个点都走过了;
所以最后的答案就是f[(1<<n)-1][a],a就是以每个数(除起点)作为终止点的所有情况,你要从里面挑出一个最小值;
贴代码!!!
#include<cstdio> #include<iostream> using namespace std; const int maxn=20; int n; double f[1<<maxn][maxn]; //第一维度表示一共有2^maxn-1种情况,第二维度表示共只有maxn种可能的终止点 double dis(int i,int j) //一个求距离的函数 { return sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]));//两点间距离公式求最短距离 } int main() { cin >> n; for (int a=0;a<n;a++) //注意以0开始比较好写代码 cin >> x[a] >> y[a]; //输入横纵坐标 for (int a=0;a<(1<<n);a++) //1<<n就相当于是2^n for (int b=0;b<n;b++) f[a][b] = 1e+20; //初始化为无穷大 f[1][0] = 0; //起点到自己的距离为0 for (int s=1;s<(1<<n);s++) //从第一种情况枚举到最后一种情况 for (int i=0;i<n;i++) //枚举每个点 if ( ((s>>i) & 1) == 1) //如果这个点我们已经到过了,则我们可以从它开始继续往下走 for (int j=0;j<n;j++) //找出没有走过的点 if ( ((s>>j) & 1) == 0) //如果j点没有被访问过 f[s|(1<<j)][j] = min(f[s|(1<<j)][j] , f[s][i] + dis(i,j)); //非常重要的状态转移方程! //s|(1<<j)表示将s的第j位改成1,那么将状态改为"到达过j且经过的最后一个点为j"的最短路为min(它原本的值,从起点到i的值+i与j的距离) double ans = 1e+20; //因为我们后面要对ans进行取最小值,所以要把它设为无穷大 for (int a=1;a<n;a++) ans = min (ans , f[(1<<n)-1][a]); //从以每个除了起点的点作为终止点这n-1种情况中选择一个最短路径 cout << ans <<endl; //输出最短路 return 0; }
5.普通DP

首先看一下边界条件:
第一行与第一列的方案数只能为1:f[i][1]=f[1][j]=1;
为什么呢?因为你只能往下或往右走,而你要想在第一行你只能一直往右走,没有其他走法;同理你想要在第一列你也只能一直往下走,没有其他的走法;
而对于其余的任何点,它可以看做是左边的点向右走得来的,也可以看做是从上面的点得来的,所以到这个点的方案数就是当它左边点的方案数+到它右边点的方案数
那么就得出了状态转移方程:
f[i][j]=f[i-1][j]+f[i][f-1] i,j>1
那么这个题就做完了!




边界条件:f[1][1]=a[1,1]
因为一个点只能从左上或正上面走过来,所以对这两条路径取最大值再加上这个点的权值就是从起点到这个点的最大权值!


对于这个题要求的是mod m之后的最大值,所以我们就不能再像之前那个题一样做了。
Why?
因为两个数mod一个数后,大小关系就不确定了。

例如有两个数5和14,分别对6取模:
5%6=5
14%6=2
如果按照上面的取大数再取模,显然最后算出的答案是错的!
那咋办泥?
用zhx思想既然题目多了一个取模条件,所以我们只要加一个维度就好啦!
我们用F[i][j][k]表示走到第i行第j列是否可能存在%m==k的情况,1(true)为可能,0(false)为不可能


注意取模(有可能是负数)


首先我们要保证这是个上升序列qwq,就是对于这个序列中的一个元素i,你要从这个序列里找出一个最大的小于它的值j然后接在他后面,序列长度+1

状态转移方程:

时间复杂度:O(n^2)
背包问题


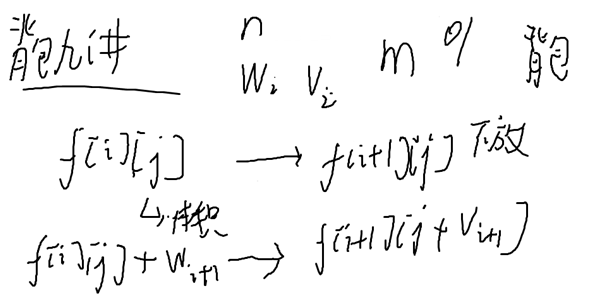
状态转移方程:




我们定义状态f[i][j][k]表示已经填到第i位,已经填的x是否大于v(0大于,1等于),每一位乘积是多少

1~9这几个数中质因数只有2,3,5,7!
所以乘积写出来一定是:

那么这样,我们修改一下状态:
将一个维度拆成了四个维度。。。

普通像我一样的蒟蒻:老师,多开了数组不会炸嘛???
还在上小学的zhx:因为里面存的数直接降到log级别,所以不但复杂度没有升高,还降低了!!!所以说维度高复杂度不一定高!!

完喽qwq~~

