清明培训 清北学堂 DAY2
今天是钟皓曦老师的讲授~~
总结了一下今天的内容：
数论！！！
1.整除性
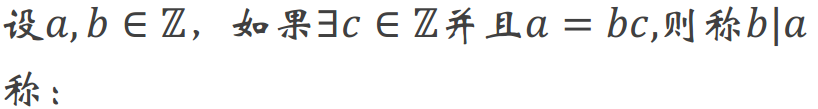
2.质数
定义：
性质： 
3.整数分解定理——算数基本定理
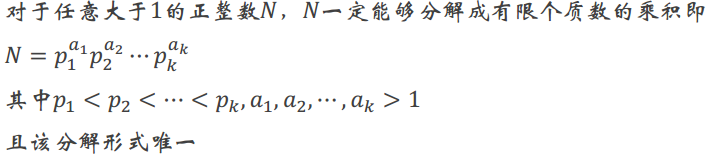
证明：
存在性：
设N是最小不满足唯一分解定理的整数
（1） 若N为质数，则N=N¹，所以N不存在；
（2） 若N为合数，则N=P*（N/P），因为N/P也是不满足定理的整数
所以与N是不满足定理的最小整除相矛盾
所以N不存在
唯一性：
4.素数的判定
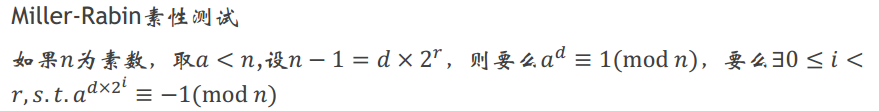（注：s.t.是“使得”的意思）
根据钟神长者的小学经验：取2,3,5,7,13,29,37,89这8个素数在int范围内是100%准的
时间复杂度为O（klogn）
怎么代码实现呢？？？
首先我们要先求出d和r，然后快速幂求出a^d和a^（d*2^i）
a^（d*2^i）当然有别的好方法求啦，看下面：
a^（d*2^（i-1）*2）=（a^（d*2^（i-1）））^2=（（a^（d*2^（i-2）））^2）^2……最后搞下去就变成了a^（d*2^i）
所以我们只要把快速幂后的a^（d*2^i）再进行快速幂就行啦
程序代码：
int gg[8] = {2,3,5,7,13,29,37,89}; //8个好用的素数
bool miller_rabin(int a,int n)
{
int d=n-1,r=0;
while (d%2==0)
d/=2,r++; //求d和r
int x = kuaisumi(a,d,n); //快速幂a^d
if (x==1) return true; //判断a^d%n是否为1，若是，则可能是质数；若否，进行下一层判断
for (int i=0;i<r;i++)
{
if (x==n-1) return true;
x=(long long)x*x%n; //将a^d进行快速幂来判断a^（d*2^i）%n是否为-1也就是n-1；
}
return false;
}
bool is_prime(int n)
{
if (n<=1) return false;
for (int a=0;a<8;a++)
if (n==gg[a]) return true; //判断n是否为列举的素数中的任何一个，若是则直接判为素数
for (int a=0;a<8;a++)
if (!miller_rabin(gg[a],n)) return false; //进行miller_rabin素数检查
return true;
}
int kuaisumi（int a,int d,int n） { //快速幂函数
int ans=1;
while(b)
{
if(b&1) ans=ans*a%n;
a=a*a%n;
b>>=1;
}
5.裴蜀定理
设d=gcd（a，b）；
6.扩展欧几里得
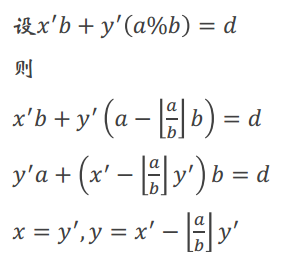
程序代码：
第10行和第4行都是返回的最大公约数，而x，y的值都地址返回了
7.中国剩余定理
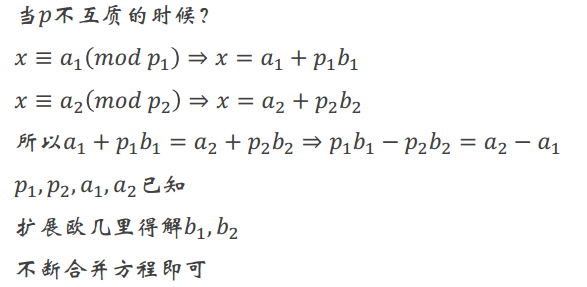
另外我们还可以用大数翻倍法做
8.逆元
定义：
我们都知道欧拉定理：
怎么证呢？？？
（1） 
那么
都<n且都与n互质
所以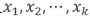
对于mod n是不同余的
那么同乘a也是不同余的
那么这其中的任何
这样我们得到了
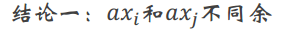
既然这其中的任何，那么
这样我们得到了
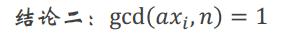
每一个乘a后mod n的余数不变，那么我们可以说
这样我们就得到了
由此我们就可以得到：
9.Miller_Rabin 二次侦探定理
说明一下： x²≡1 （mod p）
x²-1≡0 （mod p）
（x+1）（x-1）≡0 （mod p）
x≡1或-1
a^（d*2^r）-1≡0 （mod p）
（a^（d*2^（r-1））-1）（a^（d*2^（r-1））+1）≡0 （mod p）
a^（d*2^（r-1））≡1或a^（d*2^（r-1））≡-1
若a^（d*2^（r-1））≡-1，则满足Miller_Rabin的第二个式子，直接判定n为质数
否则a^（d*2^（r-1））≡1
a^（d*2^（r-1））-1≡0 （mod p）
(a^（d*2^（r-2））+1)(a^（d*2^（r-2））-1)≡0 (mod p）
a^（d*2^（r-2））≡1或a^（d*2^（r-2））≡-1
若a^（d*2^（r-2））≡-1，则满足Miller_Rabin的第二个式子，直接判定n为质数
否则a^（d*2^（r-2））≡1
……
10.线性求逆元
程序代码：
int inv[i]=1；
for(int i=2;i<=10;i++)
{
inv[i]=(p-(p/i))*inv[p%i]%p;
}
11.BSGS算法
先来引入积性函数和完全积性函数的概念：
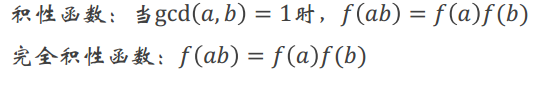
以下是几个常见的积性函数：
可能大家对莫比乌斯函数μ（n）不大熟悉，我来给大家介绍一下：
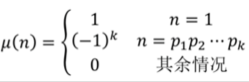
我们来了解一下莫比乌斯函数的性质
答案很简单：当n=1时，答案为1；当n不为1时，答案为0；
莫比乌斯反演
F(n)和f(n)为算术函数，若他们满足
则有
