【NOIP 2015】 运输计划
题目描述
L 国有 n 个星球,还有 n-1 条双向航道,每条航道建立在两个星球之间,这 n-1 条航道连通了 L 国的所有星球。
小 P 掌管一家物流公司,该公司有很多个运输计划,每个运输计划形如:有一艘物
流飞船需要从 ui 号星球沿最快的宇航路径飞行到 vi 号星球去。显然,飞船驶过一条航道 是需要时间的,对于航道 j,任意飞船驶过它所花费的时间为 tj,并且任意两艘飞船之 间不会产生任何干扰。
为了鼓励科技创新,L 国国王同意小 P 的物流公司参与 L 国的航道建设,即允许小 P 把某一条航道改造成虫洞,飞船驶过虫洞不消耗时间。
在虫洞的建设完成前小 P 的物流公司就预接了 m 个运输计划。在虫洞建设完成后, 这 m 个运输计划会同时开始,所有飞船一起出发。当这 m 个运输计划都完成时,小 P 的 物流公司的阶段性工作就完成了。
如果小 P 可以自由选择将哪一条航道改造成虫洞,试求出小 P 的物流公司完成阶段 性工作所需要的最短时间是多少?
输入输出格式
输入格式：
输入文件名为 transport.in。
第一行包括两个正整数 n、m,表示 L 国中星球的数量及小 P 公司预接的运输计划的数量,星球从 1 到 n 编号。
接下来 n-1 行描述航道的建设情况,其中第 i 行包含三个整数 ai, bi 和 ti,表示第
i 条双向航道修建在 ai 与 bi 两个星球之间,任意飞船驶过它所花费的时间为 ti。
接下来 m 行描述运输计划的情况,其中第 j 行包含两个正整数 uj 和 vj,表示第 j个 运输计划是从 uj 号星球飞往 vj 号星球。
输出格式：
输出文件名为 transport.out。
共 1 行,包含 1 个整数,表示小 P 的物流公司完成阶段性工作所需要的最短时间。
输入输出样例
6 3 1 2 3 1 6 4 3 1 7 4 3 6 3 5 5 3 6 2 5 4 5
11
说明
所有测试数据的范围和特点如下表所示
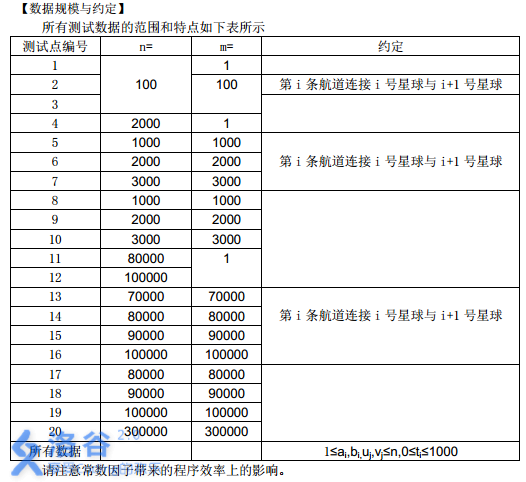
请注意常数因子带来的程序效率上的影响。
=======================================我是分割线============================================
嗯，只要有思路，那这题一定是想到lca的吧。。。（不会lca的请移步度娘）
然后我们就有了一种思想：枚举最长航线经过的所有线段，并计算删去后当前最长。这样复杂度应该是平均O(M^2)，好像乱搞搞能五十QAQ（但大数据会TLE+MLE）。
然后我们来想想300000的数据需要什么复杂度：最小估计是要O(log(N)^2*M)。等等，两个log？二分答案？
好，那我们就来二分一下答案。
那么，容易想到，只要对长度大于ans的进行判断就行了。那么对所有长度大于ans的路径求一个交，然后枚举删去交中的哪条边就行了。那么二分的判断条件是交中是否存在边w使max(路径长度)-ans<=w
那么，我们就有了一个复杂度为（m*log^n(n)）的算法。
