scikit-learn中的无监督聚类算法

　　scikit-learn主要由分类、回归、聚类和降维四大部分组成，其中分类和回归属于有监督学习范畴，聚类属于无监督学习范畴，降维适用于有监督学习和无监督学习。scikit-learn的结构示意图如下所示：

 

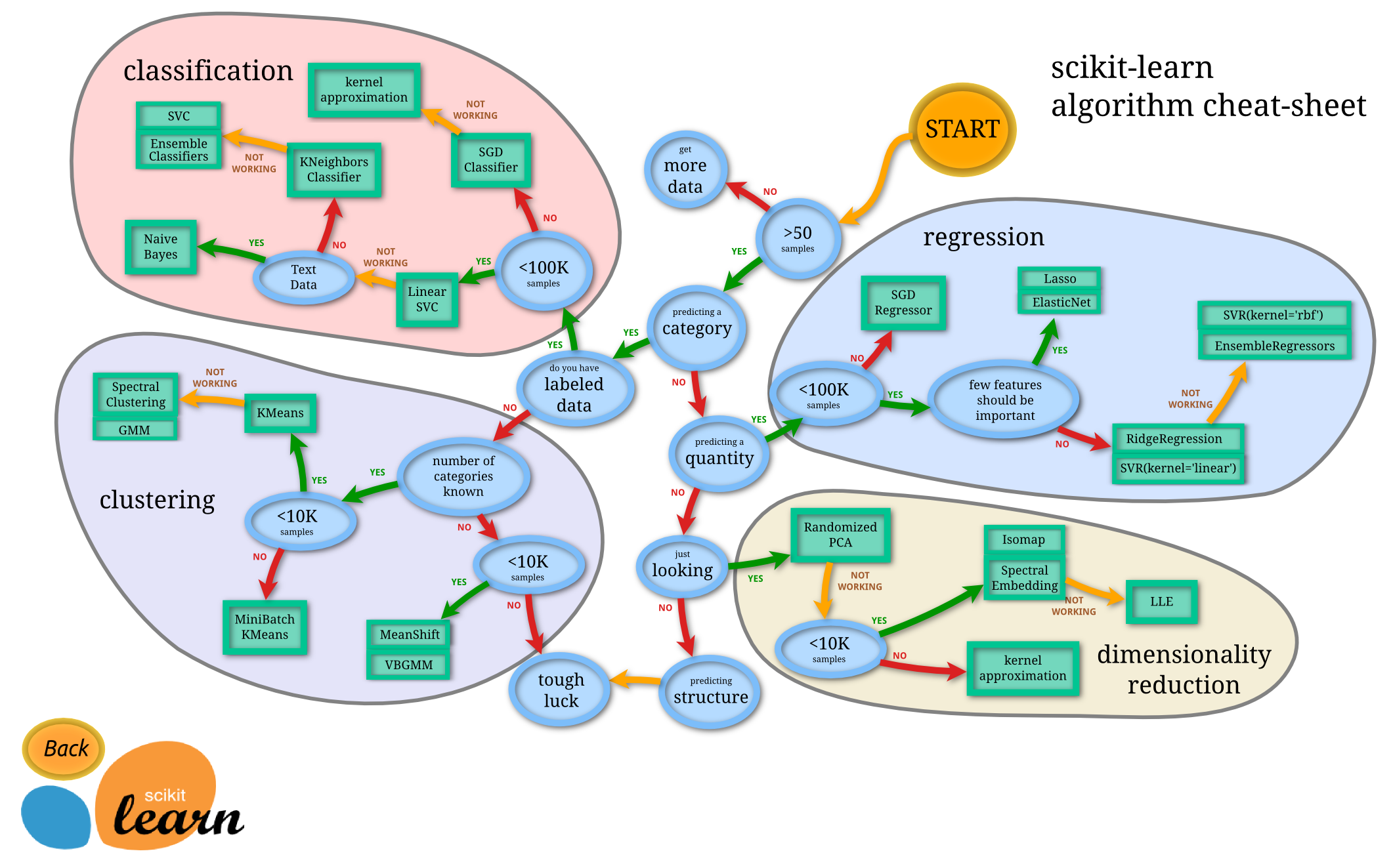
　　scikit-learn中的聚类算法主要有：

• K-Means(cluster.KMeans)
• AP聚类（cluster.AffinityPropagation）
• 均值漂移（cluster.MeanShift）
• 层次聚类（cluster.AgglomerativeClustering）
• DBSCAN（cluster.DBSCAN）
• BRICH（cluster.Brich）
• 谱聚类（cluster.Spectral.Clustering）
• 高斯混合模型（GMM）∈期望最大化（EM）算法（mixture.GaussianMixture）

 

1. K-Means

1.1 简介

　　K 均值聚类（K-Means Clustering）是最基础和最经典的基于划分的聚类算法，是十大经典数据挖掘算法之一。它的基本思想是，通过迭代方式寻找K个簇的一种划分方案，使得聚类结果对应的代价函数最小。特别地，代价函数可以定义为各个样本距离所属簇中心点的误差平方和（SSE）。

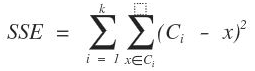
1.2 算法原理

1. 数据预处理，如归一化、离散点处理等（优化）
2. 随机选择k个簇的质心
3. 遍历所有样本，把样本划分到距离最近的一个质心
4. 划分之后就有K个簇，计算每个簇的平均值作为新的质心
5. 重复步骤3、4，直到达到停止条件

迭代停止条件：

• 聚类中心不再发生变化
• 所有的距离最小
• 迭代次数达到设定值

1.3 算法特点

• Distances between points（点之间的距离）

优点：

• 算法容易理解，聚类效果不错
• 具有出色的速度：O(NKt)
• 当簇近似高斯分布时，效果比较好

缺点：

• 需要人工预先确定初试K值，且该值和真是的数据分布未必吻合
• 对初始中心点敏感
• 不适合发现非凸形状的簇或者大小差别较大的簇
• 特殊值/离散值（噪点）对模型的影响比较大
• 算法只能收敛到局部最优，效果受初始值影响很大
•  从数据先验的角度来说，在 Kmeans 中,我们假设各个 cluster 的先验概率是一样的,但是各个 cluster 的数据量可能是不均匀的。举个例子,cluster A 中包含了10000个样本,cluster B 中只包含了100个。那么对于一个新的样本,在不考虑其与A cluster、 B cluster 相似度的情况,其属于 cluster A 的概率肯定是要大于 cluster B的。

1.4  适用场景

• 通用, 均匀的 cluster size（簇大小）, flat geometry（平面几何）, 不是太多的 clusters（簇）
• 非常大的 n_samples、中等的 n_clusters 使用 MiniBatch code
• 样本量<10K时使用k-means，>=10K时用MiniBatchKMeans
• 不太适用于离散分类

1.5 测试代码

print(__doc__)

# Author: Phil Roth <mr.phil.roth@gmail.com>
# License: BSD 3 clause

import numpy as np
import matplotlib.pyplot as plt

from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

plt.figure(figsize=(12, 12))

n_samples = 1500
random_state = 170
X, y = make_blobs(n_samples=n_samples, random_state=random_state)

# Incorrect number of clusters
y_pred = KMeans(n_clusters=2, random_state=random_state).fit_predict(X)

plt.subplot(221)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.title("Incorrect Number of Blobs")

# Anisotropicly distributed data
transformation = [[0.60834549, -0.63667341], [-0.40887718, 0.85253229]]
X_aniso = np.dot(X, transformation)
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_aniso)

plt.subplot(222)
plt.scatter(X_aniso[:, 0], X_aniso[:, 1], c=y_pred)
plt.title("Anisotropicly Distributed Blobs")

# Different variance
X_varied, y_varied = make_blobs(n_samples=n_samples,
                                cluster_std=[1.0, 2.5, 0.5],
                                random_state=random_state)
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_varied)

plt.subplot(223)
plt.scatter(X_varied[:, 0], X_varied[:, 1], c=y_pred)
plt.title("Unequal Variance")

# Unevenly sized blobs
X_filtered = np.vstack((X[y == 0][:500], X[y == 1][:100], X[y == 2][:10]))
y_pred = KMeans(n_clusters=3,
                random_state=random_state).fit_predict(X_filtered)

plt.subplot(224)
plt.scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_pred)
plt.title("Unevenly Sized Blobs")

plt.show()

 

2. AP聚类

2.1 简介

 　　AP(Affinity Propagation)通常被翻译为近邻传播算法或者亲和力传播算法，是在2007年的Science杂志上提出的一种新的聚类算法。AP算法的基本思想是将全部数据点都当作潜在的聚类中心(称之为exemplar)，然后数据点两两之间连线构成一个网络(相似度矩阵)，再通过网络中各条边的消息(responsibility和availability)传递计算出各样本的聚类中心。

2.2 算法原理

3个概念：

• 吸引度（responsibility）矩阵R：其中r(i,k)描述了数据对象k适合作为数据对象i的聚类中心的程度，表示的是从i到k的消息。
• 归属度（availability）矩阵A：其中a(i,k)描述了数据对象i选择数据对象k作为其据聚类中心的适合程度，表示从k到i的消息。
• 相似度（similarity）矩阵S：通常S（i，j）取i，j的欧氏距离的负值，当i=j时，通常取整个矩阵的最小值或者中位数(Scikit-learn中默认为中位数)，取得值越大则最终产生的类数量越多。

算法步骤：

1. 算法初始，吸引度矩阵和归属度矩阵均初始化为0矩阵。

2. 更新吸引度矩阵

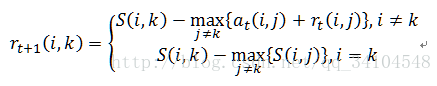
3. 更新归属度矩阵

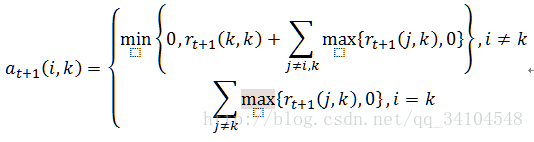
4. 根据衰减系数λ对两个公式进行衰减

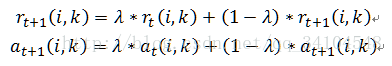
5. 重复步骤2/3/4直至矩阵稳定或者达到最大迭代次数，算法结束。最终取a+r最大的k作为聚类中心。

2.3 算法特点

• Graph distance (e.g. nearest-neighbor graph)（图形距离（例如，最近邻图））

优点：

• 与其他聚类算法不同,AP聚类不需要指定K(经典的K-Means)或者是其他描述聚类个数的参数
• 一个聚类中最具代表性的点在AP算法中叫做Examplar,与其他算法中的聚类中心不同,examplar是原始数据中确切存在的一个数据点,而不是由多个数据点求平均而得到的聚类中心
• 多次执行AP聚类算法,得到的结果完全一样的，即不需要进行随机选取初值步骤.
• AP算法相对于Kmeans优势是不需要指定聚类数量,对初始值不敏感
• 模型对数据的初始值不敏感。
• 对初始相似度矩阵数据的对称性没有要求。
• 相比与k-centers聚类方法，其结果的平方差误差较小。

缺点：

• AP算法需要事先计算每对数据对象之间的相似度，如果数据对象太多的话，内存放不下，若存在数据库，频繁访问数据库也需要时间。
• AP算法的时间复杂度较高，一次迭代大概O(N3)
• 聚类的好坏受到参考度和阻尼系数的影响

2.4 适用场景

• 许多簇，不均匀的簇大小，非平面几何
• 不可扩展的 n_samples
• 特别适合高维、多类数据快速聚类
• 图像、文本、生物信息学、人脸识别、基因发现、搜索最优航线、 码书设计以及实物图像识别等领域

2.5 测试代码

# -*- coding:utf-8 -*-
 
import numpy as np
import matplotlib.pyplot as plt
import sklearn.datasets as ds
import matplotlib.colors
from sklearn.cluster import AffinityPropagation
from sklearn.metrics import euclidean_distances
 
#聚类算法之AP算法:
#1--与其他聚类算法不同,AP聚类不需要指定K(金典的K-Means)或者是其他描述聚类个数的参数
#2--一个聚类中最具代表性的点在AP算法中叫做Examplar,与其他算法中的聚类中心不同,examplar
#是原始数据中确切存在的一个数据点,而不是由多个数据点求平均而得到的聚类中心
#3--多次执行AP聚类算法,得到的结果完全一样的，即不需要进行随机选取初值步骤.
#算法复杂度较高,为O(N*N*logN),而K-Means只是O(N*K)的复杂度，当N》3000时,需要算很久
#AP算法相对于Kmeans优势是不需要指定聚类数量,对初始值不敏感
 
#AP算法应用场景：图像、文本、生物信息学、人脸识别、基因发现、搜索最优航线、 码书设计以及实物图像识别等领域
 
#算法详解: http://blog.csdn.net/helloeveryon/article/details/51259459
 
if __name__=='__main__':
    #scikit中的make_blobs方法常被用来生成聚类算法的测试数据，直观地说，make_blobs会根据用户指定的特征数量、
    # 中心点数量、范围等来生成几类数据，这些数据可用于测试聚类算法的效果。
    #函数原型：sklearn.datasets.make_blobs(n_samples=100, n_features=2,
    # centers=3, cluster_std=1.0, center_box=(-10.0, 10.0), shuffle=True, random_state=None)[source]
    #参数解析：
    # n_samples是待生成的样本的总数。
    #
    # n_features是每个样本的特征数。
    #
    # centers表示类别数。
    #
    # cluster_std表示每个类别的方差，例如我们希望生成2类数据，其中一类比另一类具有更大的方差，可以将cluster_std设置为[1.0, 3.0]。
 
    N=400
    centers = [[1, 2], [-1, -1], [1, -1], [-1, 1]]
    #生成聚类算法的测试数据
    data,y=ds.make_blobs(N,n_features=2,centers=centers,cluster_std=[0.5, 0.25, 0.7, 0.5],random_state=0)
    #计算向量之间的距离
    m=euclidean_distances(data,squared=True)
    #求中位数
    preference=-np.median(m)
    print 'Preference:',preference
 
    matplotlib.rcParams['font.sans-serif'] = [u'SimHei']
    matplotlib.rcParams['axes.unicode_minus'] = False
    plt.figure(figsize=(12,9),facecolor='w')
    for i,mul in enumerate(np.linspace(1,4,9)):#遍历等差数列
        print 'mul=',mul
        p=mul*preference
        model=AffinityPropagation(affinity='euclidean',preference=p)
        af=model.fit(data)
        center_indices=af.cluster_centers_indices_
        n_clusters=len(center_indices)
        print ('p=%.1f'%mul),p,'聚类簇的个数为:',n_clusters
        y_hat=af.labels_
 
        plt.subplot(3,3,i+1)
        plt.title(u'Preference：%.2f，簇个数：%d' % (p, n_clusters))
        clrs=[]
        for c in np.linspace(16711680, 255, n_clusters):
            clrs.append('#%06x' % c)
            for k, clr in enumerate(clrs):
                cur = (y_hat == k)
                plt.scatter(data[cur, 0], data[cur, 1], c=clr, edgecolors='none')
                center = data[center_indices[k]]
                for x in data[cur]:
                    plt.plot([x[0], center[0]], [x[1], center[1]], color=clr, zorder=1)
            plt.scatter(data[center_indices, 0], data[center_indices, 1], s=100, c=clrs, marker='*', edgecolors='k',
                        zorder=2)
            plt.grid(True)
        plt.tight_layout()
        plt.suptitle(u'AP聚类', fontsize=20)
        plt.subplots_adjust(top=0.92)
        plt.show()

 

3. 均值漂移（Mean-shift）

3.1 简介

　　Mean-shift（即：均值迁移）的基本思想：在数据集中选定一个点，然后以这个点为圆心，r为半径，画一个圆(二维下是圆)，求出这个点到所有点的向量的平均值，而圆心与向量均值的和为新的圆心，然后迭代此过程，直到满足一点的条件结束。(Fukunage在1975年提出)

　　后来Yizong Cheng 在此基础上加入了 核函数 和 权重系数 ，使得Mean-shift 算法开始流行起来。目前它在聚类、图像平滑、分割、跟踪等方面有着广泛的应用。

3.2 算法原理

　　为了方便大家理解，借用下几张图来说明Mean-shift的基本过程。

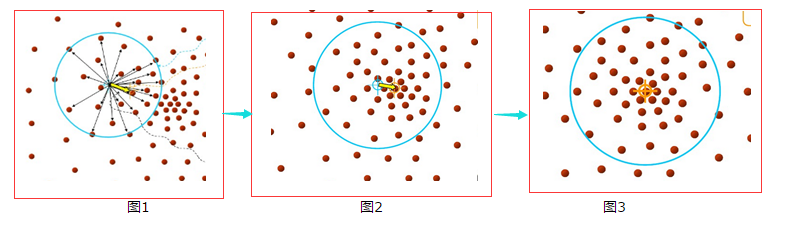
　　由上图可以很容易看到，Mean-shift 算法的核心思想就是不断的寻找新的圆心坐标，直到密度最大的区域。

3.3 算法特点

• Distances between points（点之间的距离）
• 圆心(或种子)的确定和半径(或带宽)的选择，是影响算法效率的两个主要因素。
• 该算法不是高度可扩展的，因为在执行算法期间需要执行多个最近邻搜索。
• 该算法保证收敛，但是当质心的变化较小时，算法将停止迭代。
• 通过找到给定样本的最近质心来给新样本打上标签。

3.4 适用场景

• 许多簇，不均匀的簇大小，非平面几何
• 不可扩展的 n_samples
• 适用于类别数量未知，且样本数量<10K
• 目前它在聚类、图像平滑、分割、跟踪等方面有着广泛的应用。

3.5 测试代码

print(__doc__)

import numpy as np
from sklearn.cluster import MeanShift, estimate_bandwidth
from sklearn.datasets.samples_generator import make_blobs

# #############################################################################
# Generate sample data
centers = [[1, 1], [-1, -1], [1, -1]]
X, _ = make_blobs(n_samples=10000, centers=centers, cluster_std=0.6)

# #############################################################################
# Compute clustering with MeanShift

# The following bandwidth can be automatically detected using
bandwidth = estimate_bandwidth(X, quantile=0.2, n_samples=500)

ms = MeanShift(bandwidth=bandwidth, bin_seeding=True)
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_

labels_unique = np.unique(labels)
n_clusters_ = len(labels_unique)

print("number of estimated clusters : %d" % n_clusters_)

# #############################################################################
# Plot result
import matplotlib.pyplot as plt
from itertools import cycle

plt.figure(1)
plt.clf()

colors = cycle('bgrcmykbgrcmykbgrcmykbgrcmyk')
for k, col in zip(range(n_clusters_), colors):
    my_members = labels == k
    cluster_center = cluster_centers[k]
    plt.plot(X[my_members, 0], X[my_members, 1], col + '.')
    plt.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,
             markeredgecolor='k', markersize=14)
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()

 

4. 层次聚类

4.1 简介

　　Hierarchical Clustering(层次聚类)：就是按照某种方法进行层次分类，直到满足某种条件为止。

　　主要分为两类：

1. 凝聚：从下到上。首先将每个对象作为一个簇，然后合并这些原子簇为越来越大的簇，直到所有的对象都在一个簇中，或者某个终结条件被满足。
2. 分裂：从上到下。首先将所有对象置于同一个簇中，然后逐渐细分为越来越小的簇，直到每个对象自成一簇，或者达到了某个终止条件。（较少用）

4.2 算法原理（凝聚）

1. 将每个对象归为一类, 共得到N类, 每类仅包含一个对象. 类与类之间的距离就是它们所包含的对象之间的距离.
2. 找到最接近的两个类并合并成一类, 于是总的类数少了一个.
3. 重新计算新的类与所有旧类之间的距离.
4. 重复第2步和第3步, 直到最后合并成一个类为止(此类包含了N个对象).

图解过程：

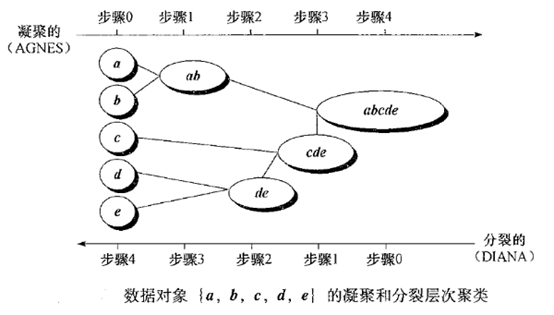
4.3 算法特点

• Distances between points（点之间的距离）

4.4 适用场景

• 很多的簇，可能连接限制
• 大的 n_samples 和 n_clusters

4.5 测试代码

# Authors: Gael Varoquaux
# License: BSD 3 clause (C) INRIA 2014

print(__doc__)
from time import time

import numpy as np
from scipy import ndimage
from matplotlib import pyplot as plt

from sklearn import manifold, datasets

digits = datasets.load_digits(n_class=10)
X = digits.data
y = digits.target
n_samples, n_features = X.shape

np.random.seed(0)

def nudge_images(X, y):
    # Having a larger dataset shows more clearly the behavior of the
    # methods, but we multiply the size of the dataset only by 2, as the
    # cost of the hierarchical clustering methods are strongly
    # super-linear in n_samples
    shift = lambda x: ndimage.shift(x.reshape((8, 8)),
                                  .3 * np.random.normal(size=2),
                                  mode='constant',
                                  ).ravel()
    X = np.concatenate([X, np.apply_along_axis(shift, 1, X)])
    Y = np.concatenate([y, y], axis=0)
    return X, Y


X, y = nudge_images(X, y)


#----------------------------------------------------------------------
# Visualize the clustering
def plot_clustering(X_red, labels, title=None):
    x_min, x_max = np.min(X_red, axis=0), np.max(X_red, axis=0)
    X_red = (X_red - x_min) / (x_max - x_min)

    plt.figure(figsize=(6, 4))
    for i in range(X_red.shape[0]):
        plt.text(X_red[i, 0], X_red[i, 1], str(y[i]),
                 color=plt.cm.nipy_spectral(labels[i] / 10.),
                 fontdict={'weight': 'bold', 'size': 9})

    plt.xticks([])
    plt.yticks([])
    if title is not None:
        plt.title(title, size=17)
    plt.axis('off')
    plt.tight_layout(rect=[0, 0.03, 1, 0.95])

#----------------------------------------------------------------------
# 2D embedding of the digits dataset
print("Computing embedding")
X_red = manifold.SpectralEmbedding(n_components=2).fit_transform(X)
print("Done.")

from sklearn.cluster import AgglomerativeClustering

for linkage in ('ward', 'average', 'complete', 'single'):
    clustering = AgglomerativeClustering(linkage=linkage, n_clusters=10)
    t0 = time()
    clustering.fit(X_red)
    print("%s :\t%.2fs" % (linkage, time() - t0))

    plot_clustering(X_red, clustering.labels_, "%s linkage" % linkage)


plt.show()

 

5. DBSCAN

5.1 简介

　　DBSCAN（Density-Based Spatial Clustering of Applications with Noise,具有噪声的基于密度的聚类方法）是一种基于密度的空间聚类算法。该算法将具有足够密度的区域划分为簇(即要求聚类空间中的一定区域内所包含对象的数目不小于某一给定阈值)，并在具有噪声的空间数据库中发现任意形状的簇，它将簇定义为密度相连的点的最大集合。

5.2 算法原理

　　算法步骤：

　　DBSCAN需要二个参数:扫描半径 (eps)和最小包含点数(min_samples)

1. 遍历所有点，寻找核心点
2. 连通核心点，并且在此过程中扩展某个分类集合中点的个数

　　图解过程：

          

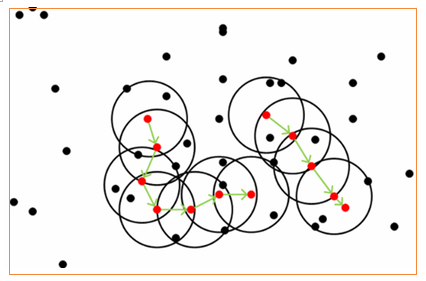
5.3 算法特点

• Distances between nearest points（最近点之间的距离）

优点：

• 可以发现任意形状的聚类

缺点：

• 随着数据量的增加，对I/O、内存的要求也随之增加。
• 如果密度分布不均匀，聚类效果较差

5.4 适用场景

• 非平面几何，不均匀的簇大小
• 非常大的 n_samples, 中等的 n_clusters

5.5 测试代码

from sklearn.datasets.samples_generator import make_blobs
from sklearn.cluster import DBSCAN
import numpy as np
import matplotlib.pyplot as plt
from itertools import cycle  ##python自带的迭代器模块
from sklearn.preprocessing import StandardScaler

##产生随机数据的中心
centers = [[1, 1], [-1, -1], [1, -1]]
##产生的数据个数
n_samples=750
##生产数据:此实验结果受cluster_std的影响，或者说受eps 和cluster_std差值影响
X, lables_true = make_blobs(n_samples=n_samples, centers= centers, cluster_std=0.4, 
                  random_state =0)


##设置分层聚类函数
db = DBSCAN(eps=0.3, min_samples=10)
##训练数据
db.fit(X)
##初始化一个全是False的bool类型的数组
core_samples_mask = np.zeros_like(db.labels_, dtype=bool)
'''
   这里是关键点(针对这行代码：xy = X[class_member_mask & ~core_samples_mask])：
   db.core_sample_indices_  表示的是某个点在寻找核心点集合的过程中暂时被标为噪声点的点(即周围点
   小于min_samples)，并不是最终的噪声点。在对核心点进行联通的过程中，这部分点会被进行重新归类(即标签
   并不会是表示噪声点的-1)，也可也这样理解，这些点不适合做核心点，但是会被包含在某个核心点的范围之内
'''
core_samples_mask[db.core_sample_indices_] = True

##每个数据的分类
lables = db.labels_

##分类个数：lables中包含-1，表示噪声点
n_clusters_ =len(np.unique(lables)) - (1 if -1 in lables else 0)

##绘图
unique_labels = set(lables)
'''
   1)np.linspace 返回[0,1]之间的len(unique_labels) 个数
   2)plt.cm 一个颜色映射模块
   3)生成的每个colors包含4个值，分别是rgba
   4)其实这行代码的意思就是生成4个可以和光谱对应的颜色值
'''
colors = plt.cm.Spectral(np.linspace(0, 1, len(unique_labels)))

plt.figure(1)
plt.clf()


for k, col in zip(unique_labels, colors):
    ##-1表示噪声点,这里的k表示黑色
    if k == -1:
        col = 'k'

    ##生成一个True、False数组，lables == k 的设置成True
    class_member_mask = (lables == k)
    
    ##两个数组做&运算，找出即是核心点又等于分类k的值  markeredgecolor='k',
    xy = X[class_member_mask & core_samples_mask]
    plt.plot(xy[:, 0], xy[:, 1], 'o', c=col,markersize=14)
    '''
       1)~优先级最高，按位对core_samples_mask 求反，求出的是噪音点的位置
       2)& 于运算之后，求出虽然刚开始是噪音点的位置，但是重新归类却属于k的点
       3)对核心分类之后进行的扩展
    '''
    xy = X[class_member_mask & ~core_samples_mask]     
    plt.plot(xy[:, 0], xy[:, 1], 'o', c=col,markersize=6)
    
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()

 

6. BRICH

6.1 简介

　　Birch(利用层次方法的平衡迭代规约和聚类)：就是通过聚类特征(CF)形成一个聚类特征树，root层的CF个数就是聚类个数。

6.2 算法原理

相关概念

　　聚类特征(CF)：每一个CF是一个三元组,可以用（N，LS，SS）表示.其中N代表了这个CF中拥有的样本点的数量;LS代表了这个CF中拥有的样本点各特征维度的和向量,SS代表了这个CF中拥有的样本点各特征维度的平方和。

 

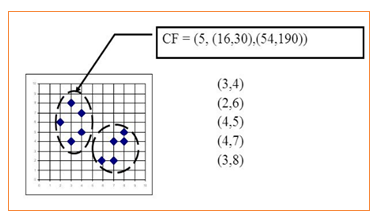
如上图所示：N = 5 

LS=(3+2+4+4+3,4+6+5+7+8)=(16,30)

SS =(32+22+42+42+32,42+62+52+72+82)=(54,190)

图解过程

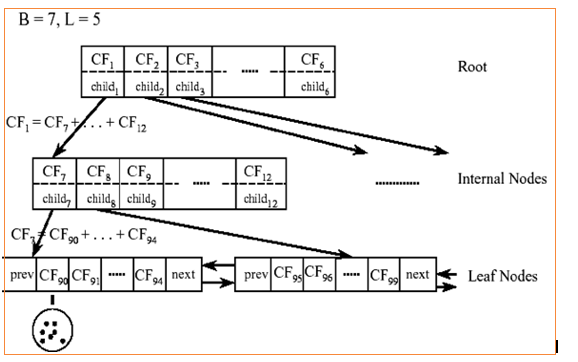
　　对于上图中的CF Tree,限定了B=7,L=5， 也就是说内部节点最多有7个CF(CF90下的圆),而叶子节点最多有5个CF(CF90到CF94)。叶子节点是通过双向链表连通的。

6.3 算法特点

• Euclidean distance between points（点之间的欧式距离）

6.4 适用场景

• 大数据集，异常值去除，数据简化
• 大的 n_clusters 和 n_samples

6.5 测试代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
from sklearn.cluster import Birch

# X为样本特征，Y为样本簇类别， 共1000个样本，每个样本2个特征，共4个簇，簇中心在[-1,-1], [0,0],[1,1], [2,2]
X, y = make_blobs(n_samples=1000, n_features=2, centers=[[-1,-1], [0,0], [1,1], [2,2]], cluster_std=[0.4, 0.3, 0.4, 0.3], 
                  random_state =9)

##设置birch函数
birch = Birch(n_clusters = None)
##训练数据
y_pred = birch.fit_predict(X)
##绘图
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()

 

7. 谱聚类

7.1 简介

　　Spectral Clustering(SC,即谱聚类)，是一种基于图论的聚类方法,它能够识别任意形状的样本空间且收敛于全局最有解，其基本思想是利用样本数据的相似矩阵进行特征分解后得到的特征向量进行聚类.它与样本特征无关而只与样本个数有关。

　　基本思路：将样本看作顶点,样本间的相似度看作带权的边,从而将聚类问题转为图分割问题:找到一种图分割的方法使得连接不同组的边的权重尽可能低(这意味着组间相似度要尽可能低),组内的边的权重尽可能高(这意味着组内相似度要尽可能高).

7.2 算法原理

 

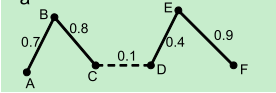
如上图所示，断开虚线，六个数据被聚成两类。

7.3 算法特点

• Graph distance (e.g. nearest-neighbor graph)（图形距离（例如最近邻图））

7.4 适用场景

• 几个簇，均匀的簇大小，非平面几何
• 中等的 n_samples, 小的 n_clusters

7.5 测试代码

from sklearn.datasets.samples_generator import make_blobs
from sklearn.cluster import spectral_clustering
import numpy as np
import matplotlib.pyplot as plt
from sklearn import metrics
from itertools import cycle  ##python自带的迭代器模块

##产生随机数据的中心
centers = [[1, 1], [-1, -1], [1, -1]]
##产生的数据个数
n_samples=3000
##生产数据
X, lables_true = make_blobs(n_samples=n_samples, centers= centers, cluster_std=0.6, 
                  random_state =0)

##变换成矩阵，输入必须是对称矩阵
metrics_metrix = (-1 * metrics.pairwise.pairwise_distances(X)).astype(np.int32)
metrics_metrix += -1 * metrics_metrix.min()
##设置谱聚类函数
n_clusters_= 4
lables = spectral_clustering(metrics_metrix,n_clusters=n_clusters_)

##绘图
plt.figure(1)
plt.clf()

colors = cycle('bgrcmykbgrcmykbgrcmykbgrcmyk')
for k, col in zip(range(n_clusters_), colors):
    ##根据lables中的值是否等于k，重新组成一个True、False的数组
    my_members = lables == k
    ##X[my_members, 0] 取出my_members对应位置为True的值的横坐标
    plt.plot(X[my_members, 0], X[my_members, 1], col + '.')
    
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()

 

8. 高斯混合模型

8.1 简介

　　高斯混合模型（Gaussian Mixture Model, GMM）也是一种常见的聚类算法，其使用了EM算法进行迭代计算。高斯混合模型假设每个簇的数据都是符合高斯分布（又叫正态分布）的，当前数据呈现的分布就是就是各个簇的高斯分布叠加在一起的结果。

8.2 算法原理

• 高斯混合模型是由K个高斯分布（正态分布）函数组成，而该算法的目的就是找出各个高斯分布最佳的均值、方差、权重。

 

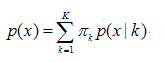
1. 指定K的值，并初始随机选择各参数的值
2. E步骤。根据当前的参数，计算每个点由某个分模型生成的概率
3. M步骤。根据E步骤估计出的概率，来改进每个分模型的均值、方差和权重
4. 重复步骤2、3，直至收敛。

8.3 算法特点

• Mahalanobis distances to centers（Mahalanobis 与中心的距离）

优点

• 可以给出一个样本属于某类的概率是多少
• 不仅用于聚类，还可用于概率密度的估计
• 可以用于生成新的样本点

缺点

• 需要指定K值
• 使用EM算法来求解
• 往往只能收敛于局部最优

8.4 适用场景

• 平面几何，适用于密度估计
• Not scalable（不可扩展）

8.5 测试代码

import matplotlib as mpl
import matplotlib.pyplot as plt

import numpy as np

from sklearn import datasets
from sklearn.mixture import GaussianMixture
from sklearn.model_selection import StratifiedKFold

print(__doc__)

colors = ['navy', 'turquoise', 'darkorange']


def make_ellipses(gmm, ax):
    for n, color in enumerate(colors):
        if gmm.covariance_type == 'full':
            covariances = gmm.covariances_[n][:2, :2]
        elif gmm.covariance_type == 'tied':
            covariances = gmm.covariances_[:2, :2]
        elif gmm.covariance_type == 'diag':
            covariances = np.diag(gmm.covariances_[n][:2])
        elif gmm.covariance_type == 'spherical':
            covariances = np.eye(gmm.means_.shape[1]) * gmm.covariances_[n]
        v, w = np.linalg.eigh(covariances)
        u = w[0] / np.linalg.norm(w[0])
        angle = np.arctan2(u[1], u[0])
        angle = 180 * angle / np.pi  # convert to degrees
        v = 2. * np.sqrt(2.) * np.sqrt(v)
        ell = mpl.patches.Ellipse(gmm.means_[n, :2], v[0], v[1],
                                  180 + angle, color=color)
        ell.set_clip_box(ax.bbox)
        ell.set_alpha(0.5)
        ax.add_artist(ell)
        ax.set_aspect('equal', 'datalim')

iris = datasets.load_iris()

# Break up the dataset into non-overlapping training (75%) and testing
# (25%) sets.
skf = StratifiedKFold(n_splits=4)
# Only take the first fold.
train_index, test_index = next(iter(skf.split(iris.data, iris.target)))


X_train = iris.data[train_index]
y_train = iris.target[train_index]
X_test = iris.data[test_index]
y_test = iris.target[test_index]

n_classes = len(np.unique(y_train))

# Try GMMs using different types of covariances.
estimators = {cov_type: GaussianMixture(n_components=n_classes,
              covariance_type=cov_type, max_iter=20, random_state=0)
              for cov_type in ['spherical', 'diag', 'tied', 'full']}

n_estimators = len(estimators)

plt.figure(figsize=(3 * n_estimators // 2, 6))
plt.subplots_adjust(bottom=.01, top=0.95, hspace=.15, wspace=.05,
                    left=.01, right=.99)


for index, (name, estimator) in enumerate(estimators.items()):
    # Since we have class labels for the training data, we can
    # initialize the GMM parameters in a supervised manner.
    estimator.means_init = np.array([X_train[y_train == i].mean(axis=0)
                                    for i in range(n_classes)])

    # Train the other parameters using the EM algorithm.
    estimator.fit(X_train)

    h = plt.subplot(2, n_estimators // 2, index + 1)
    make_ellipses(estimator, h)

    for n, color in enumerate(colors):
        data = iris.data[iris.target == n]
        plt.scatter(data[:, 0], data[:, 1], s=0.8, color=color,
                    label=iris.target_names[n])
    # Plot the test data with crosses
    for n, color in enumerate(colors):
        data = X_test[y_test == n]
        plt.scatter(data[:, 0], data[:, 1], marker='x', color=color)

    y_train_pred = estimator.predict(X_train)
    train_accuracy = np.mean(y_train_pred.ravel() == y_train.ravel()) * 100
    plt.text(0.05, 0.9, 'Train accuracy: %.1f' % train_accuracy,
             transform=h.transAxes)

    y_test_pred = estimator.predict(X_test)
    test_accuracy = np.mean(y_test_pred.ravel() == y_test.ravel()) * 100
    plt.text(0.05, 0.8, 'Test accuracy: %.1f' % test_accuracy,
             transform=h.transAxes)

    plt.xticks(())
    plt.yticks(())
    plt.title(name)

plt.legend(scatterpoints=1, loc='lower right', prop=dict(size=12))


plt.show()

 

参考

• scikit-learn官方文档（英文版）
• scikit-learn官方文档（中文版）
• 积跬步以前行的博客