机器学习入门算法

 

回归算法

线性回归：

  1.  找到一个线性变换，来预测数据点。类似于找到一直线、平面、超平面来拟合数据。
  2. 引入似然函数，根据最大化似然函数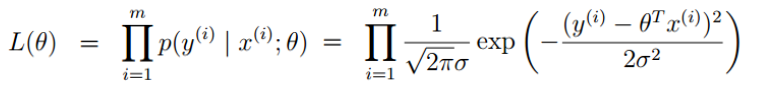似然函数，得到参数的解。
  3. 巧合的是，通过最大化似然函数解出来的参数和最小二乘法一致。

逻辑回归：经典的二分类算法

  1. 决策边界可以是非线性的
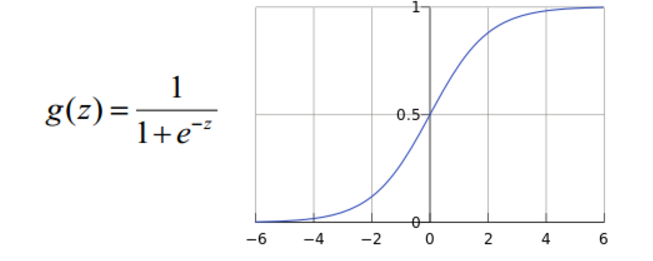
  2. 决策函数：Sigmoid Function
  3. 引入似然函数，并利用最大化似然函数，利用梯度上升迭代出理想参数。

决策树+集成算法

决策树：

  • 从根节点一步步走到叶子节点（决策）
  • 可做分类，也可做回归
  • 引入了熵来作为不确定性的度量，：H(X)=-Σ pi * log(pi)，其中pi是第i个发生的概率。
  • 信息增益（有多种计算方式ID3、C4.5、CART）为熵（不确定性）减小的程度。

  • 优化原则，先选择信息增益最大的特征。

  • 其他：GINI系数、连续数值的特征分割、剪枝策略（预剪枝、后剪枝）

贝叶斯算法：

  • 根据观测数据，推测模型参数。
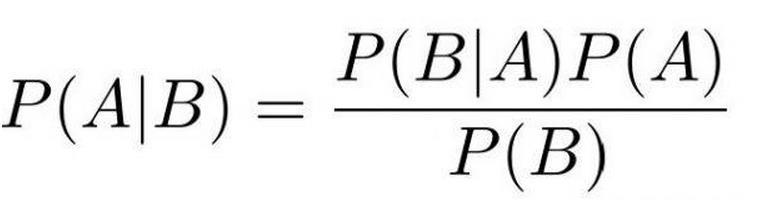
  • 朴素贝叶斯假设特征之间是独立，互不影响。
    • P(d1|h+) * P(d2|d1, h+) * P(d3|d2,d1, h+) * .. == P(d1|h+) * P(d2|h+) * P(d3|h+) * ..
  • 可于文本分析：文本关键词提取、垃圾邮件识别、新闻文章分类。

支持向量机Support Vector Machine：

  • 用直线、平面、超平面分割特征空间，已达到分类的目的。
  • 利用拉格朗日乘子法，求解出结果。
  • OpenCV中的Hog+SVM可以实现了目标检测、定位。
  • 利用其核函数，可以提高SVM的适用范围。

Ensemble Learning：

  • Bagging：训练多个分类器取平均。并联模型，同时训练。

  • Boosting：从弱学习器开始加强，通过加权来进行训练。串联模型，先后依次训练，每增加一级，都比以前更强。

  • Stacking：分2个阶段，第一阶段得出每个模型各自结果，第二阶段用前一阶段结果得出最终结果，第二阶段本身也常用机器学习的方法来预测。

降维算法

线性判别分析Linear Discriminant Analysis(LDA):

  • 将N维特征空间映射到维度更小的K维空间。
  • 是降维、分类方法之一。
  • 是有监督学习，需要事先有类标签
  • 优化目标：max. {类间方差/类内方差}，利用拉格朗日乘子法，可得（w就是矩阵的特征向量了）
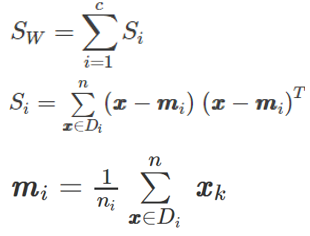
    • 其中，
    • 其中，

       

  • w就是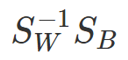的特征向量表示映射方向，λ是特征值-指示特征向量的重要程度

主成分分析Principal Component Analysis（PCA）

  • 无监督，无需事先知道标签，常用于预处理保密信息用于发布（避免泄露隐私）。
  • 降维中最常用的一种手段
  • 提取最有价值的信息（基于方差）
  • 降维后的数据，人类看着可能没有意义。
  • 步骤：
    • 求数据协方差矩阵
    • 求协方差矩阵特征值λ，特征向量c
    • 找出主特征值和特征向量（单位正交）。
    • 利用特征向量实现对原始特征降维。

聚类算法

可以这个网站上看效果：https://www.naftaliharris.com/blog/visualizing-dbscan-clustering/

K-Means:

  • 无监督问题，无需标签
  • 将相近的点分到一类，优化目标：
  • 优势
    • 简单，快速，适合常规数据集
  • 劣势
    • K值难确定
    • 复杂度与样本呈线性关系
    • 很难发现任意形状的簇

 DBSCAN算法：

  • 全名Density-Based Spatial Clustering of Applications with Noise
  • 输入参数：
    • D          - 输入数据集
    • R          - 指定半径，在P点半径R距离内的点数≥MinPts，认为P点属于某类，并具有发展"下线"的能力，其直接下线也属于该类。
    • MinPts  - 密度阈值，当P点半径R距离内的点数<MinPts，则这些新的点不具有发展下线的能力，也不属于该类。

  • 优势：

    • 不需要指定簇个数
    • 擅长找到离群点（检测任务）
    • 可以发现任意形状的簇
    • 两个参数就够了
  • 劣势：
    • 高维数据有些困难（可以做降维）
    • Sklearn中效率很慢（数据削减策略）
    • 参数难以选择（参数对结果的影响非常大）

 EM算法Expectation-Maximization：

  • 要解决的问题：
    • 求Nc个类的参数θ，Nc已知
    • 已知m个没有标记的样本。
    • 相比直接最大似然方法，少了参数标签。
  • EM算法流程
    • 初始化分布参数θ
    • E-step：根据参数θ计算每个样本属于某一类Zi的概率
    • M-Step：最大化 含有θ的似然函数（的下界），得到新的参数θ
    • 不断的迭代更新下去

GMM（高斯混合模型）

  • 要解决的问题：
    • 对样本进行分类
    • 已知类别个数，样本没有类别标签
  • GMM 由K 个Gaussian 分布组成，每个Gaussian 称为一个“Component”
  • 类似k-means方法，求解方式跟EM一样，通过迭代更新求解

用于：

  • 已知类别个数
  • 没有类别标签

神经网络

  • 反向传播
  • Softmax
  • 激活函数Sigmoid，ReLU
  • 每一层中每个节点像逻辑回归，整个网络像 逻辑回归 的 逻辑回归。
  • 案例：http://cs.stanford.edu/people/karpathy/convnetjs/demo/classify2d.html
  • 降低过拟合风险：
    • 正则化,+|W|
    • Drop-out（该方法还可以减少运算量）

Xgboost & Adaboost

将弱分类器组合成强分类器。 from xgboost import XGBClassifier

 

AIRMA（Autoregressive Integrated Moving Average Model）

自相关函数ACF(autocorrelation function)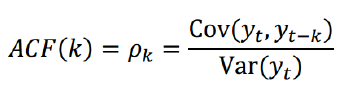

PACf vs ACF

 

CNN

RCNN(Regions with CNN features)

 

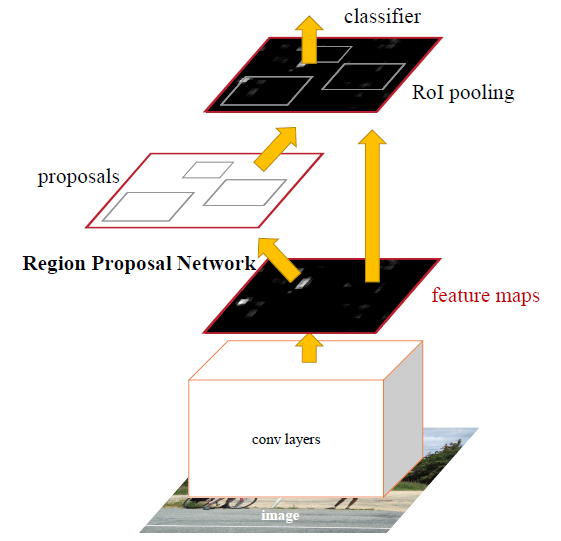
Faster R-CNN

 

深度残差网络(Deep residual network, ResNet)

 

RNN (Recurrent Neural Net)

LST（Long Short-Term Memory）= RNN的升级版，解决RNN遗忘曲线固定的问题，LSTM可学习信息 中的重要内容，舍弃不重要的内容。

 

Faster R-CNN

相比Fast R-CNN，增加了RPN

 

posted @ 2018-08-21 17:12  xbit  阅读(208)  评论(0)  编辑  收藏  举报