摘要:
1 介绍
在计算机视觉、模式识别、数据挖掘很多应用问题中,我们经常会遇到很高维度的数据,高维度的数据会造成很多问题,例如导致算法运行性能以及准确性的降低。特征选取(Feature Selection)技术的目标是找到原始数据维度中的一个有用的子集,再运用一些有效的算法,实现数据的聚类、分类以及检索等任务。
特征选取的目标是选择那些在某一特定评价标准下的最重要的特征子集。这个问题本质上是一个综合的优化问题,具有较高的计算代价。传统的特征选取方法往往是独立计算每一个特征的某一得分,然后根据得分的高低选取前k个特征。这种得分一般用来评价某一特征区分不同聚类的能力。这样的方法在二分问题中一般有不错的结果,但是在多类问题中很有可能会失败。
基于是否知道数据的lebal信息,特征提取方法可以分为有监督和无监督的方法。有监督的的特征提取方法往往通过特征与label之间的相关性来评估特征的重要性。但是label的代价是高昂的,很难在大数据集上进行计算。因此无监督的特征提取方法就显得尤为重要。无监督的方法只利用数据本身所有的信息,而无法利用数据label的信息,因此要得到更好的结果往往 阅读全文
posted @ 2012-11-27 21:46
Bin的专栏
阅读(13425)
评论(7)
推荐(4)
 通俗的讲,Precision 就是检索出来的条目中(比如网页)有多少是准确的,Recall就是所有准确的条目有多少被检索出来了。
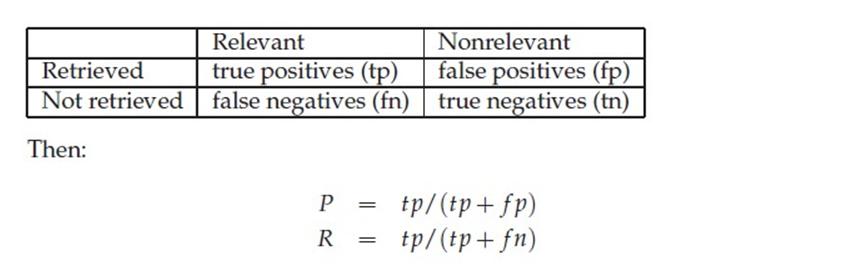
下面这张图介绍True Positive,False Negative等常见的概念,P和R也往往和它们联系起来。
通俗的讲,Precision 就是检索出来的条目中(比如网页)有多少是准确的,Recall就是所有准确的条目有多少被检索出来了。
下面这张图介绍True Positive,False Negative等常见的概念,P和R也往往和它们联系起来。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号