数据结构与算法之两种查找方法
本节的内容：
- 什么是列表查找；
- 顺序查找(线性查找)；
- 二分查找；
- 顺序查找与二分查找比较；
- 运行时间；
- 增速问题
一：什么是查找
查找：在一些数据元素中，通过一定的方法找出与给定的关键词相同的数据元素的过程。
二：顺序查找(线性查找)：从列表中查找指定的元素
定义：从列表的第一个元素开始，顺序进行搜索，直到找到元素或搜索到列表最后一个元素为止。
- 输入：列表、带查找的元素
- 输出：元素下标（未找到元素是一般返回None/-1）
- 内置列表查找函数：index()
#线性查找的代码实现
#enumerate() 函数用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列，同时列出数据和数据下标，一般用在 for 循环当中。
#教程：https://www.runoob.com/python3/python3-func-enumerate.html
num = [1,2,3,8,5]
target = 3
def linear_search(li,var):
for index,v in enumerate(li):
if v == var:
return index
return None
res = linear_search(num,target)
print(res)
#复杂度：范围是列表（n）,一个for循环====》O(n) 从头到尾遍历每个元素
三：二分查找定义
又叫折半查找，从有序列表(必须为有序)的初始候选区list[o:n]开始，通过对待查找的值与候选区中间值的比较，可以使候选区减少一半。(仅当列表为有序的时候，二分查找才管用)
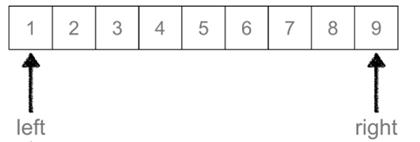
举例：从下面列表中查找3元素：
首先我们需要对候选区做一个了解，这样有助于我们更好的理解，
在上面的列表中我们使1所在的位置为left,9所在的位置为right,这样从left-right就是候选区，
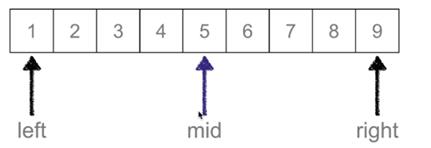
候选区中间值(mid) =（left-right）// 2;如果我们需要查找的值(val)大于候选区中间值(mid),则左边的值为：left = mid+1 ,right不变,候选区为：【(mid+1),right】；相反：查找的值(val)小于候选区中间值(mid)，则left不变，右边值为：right = mid - 1,候选区为【left, ( mid -1)】
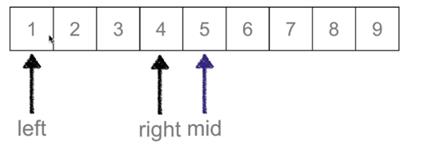
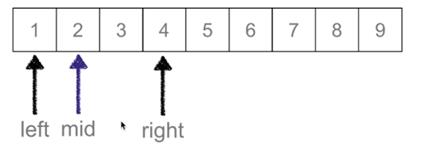
然后依次进行取值，其中left、mid、right都是指的值的下标；如果最后left>right,则表示该范围没有所需要的值。
代码如下：
num = [1,2,3,5,8]
target = 8
def Binary_search(li,val): #li传入的列表，val所需要的值
'''定义值'''
left = 0
right = len(li)-1
while left <= right: #候选区有值
mid = (right+left) // 2 #候选区中间值
if li[mid] == val:
return mid
elif li[mid] > val: #带查找的值在中间值(mid)的左侧
right = mid -1
else: #li[mid] < val 带查找的值在中间值(mid)的右侧
left = mid + 1
return None
res = Binary_search(num,target)
print(res)
四：顺序查找与二分查找比较
我们在使用大O表示法讨论运行时间时，log指的都是log2。使用简单查找法查 找元素时，在最糟情况下需要查看每个元素。
因此，如果列表包含8个数字，你最多需要检查8 个数字。而使用二分查找时，最多需要检查log n个元素。如果列表包含8个元素，你最多需要 检查3个元素，因为log 8 = 3（2^3 = 8）。如果列表包含1024个元素，你最多需要检查10个元素， 因为log 1024 = 10（2^10 =1024）。
五：两者运行时间
选择算法的时候我们本能的选择效率最高的，以最大限度的减少运行时间或者占用空间。
如果列表包含100个数字，顺序查找最多需要猜100次，40亿个数字，则最多需要才40亿次；顺序查找最多需要猜测的次数与列表长度相同==》运行时间线性时间。
二分查找的话最多猜7次，40亿最多猜32（log2^32）次===>运行时间表示为对数时间。
六：增速问题 (算法的运行时间以不同的速度增加 )
随着元素数量的增加，二分查找需要的额外时间并不多， 而顺序查找需要的额外时间却很多。因此，随着列表的增长，二分查找的速度比顺序查找快得多,但如果是无序列表，使用二分查找的话需要进行排序，两者各有优缺点，
结束：
如果你看到这里或者正好对你有所帮助，希望能点个关注或者推荐，感谢；
有错误的地方，欢迎在评论指出，作者看到会进行修改。
