空间复杂度

一：空间复杂度：用来评估算法内存占用大小的问题

空间复杂度的表示方式：

1. 使用了几个变量：O(1)；

2. 使用了长度为n的一位列表：O(n)；

3. 使用了m/n行n列的二位列表：O(mn)/O(n**2)；

公司一般采取的策略是“空间换时间”===》怎么内存大小来降低网页或者应用的打开时间/访问时间。

二：递归：

递归的特点：1). 调用自身 2). 结束条件

#当我们输入3的时候，一下代码的打印结果是什么？
def func1(x):
    if x >0:
        print(x)
        func1(x-1)
#--------------------------------
def func2(x):
    if x >0:
        func2(x-1)
        print(x)
#--------------------------------     

 

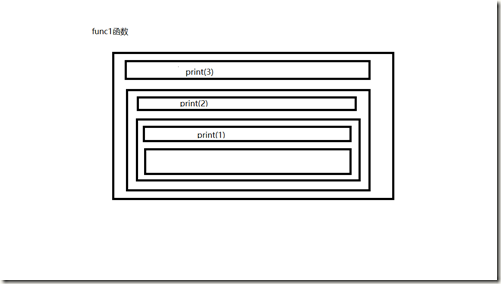
由上图可知：func1函数打印出来的是3、2、1；func2函数打印出来的是1、2、3（其中比较大的空白是递归）。

三：汉诺塔介绍及问题

汉诺塔的递归问题：

def hanio(n,a,b,c):
    if n > 0:
        hanio(n-1,a,c,b)
        print("moving %s to %s" %(a,c))
        hanio(n-1,b,a,c)

 

结果：

moving A to C
moving A to B
moving C to B
moving A to C
moving B to A
moving B to C
moving A to C