算法

一、递归

  递归实际上就是分而治之。

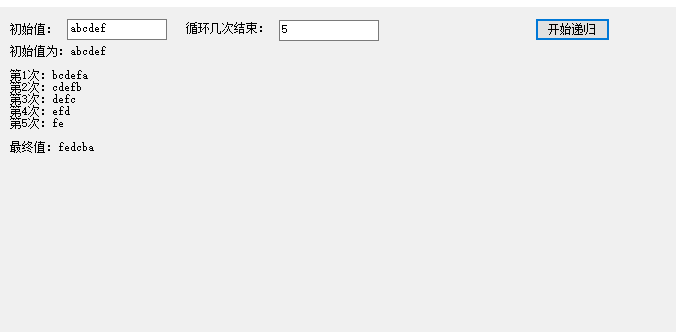
举例说明：「实现一个函数翻转给定的字符串」。假设我们要翻转的字符串是「abcdef」，那么翻转之后的结果应该是「fedcba」。毫无疑问这个字符串我们是没办法一下子就翻转过来的，那么「分而治之」吧。我们不能把多个字符一下子就完全翻转过来，但是假如字符串里的字符只有一个呢？我们翻转起来最方便了，因为什么都不用做。好了，我们可以把「abcdef」分解成「a」和「bcdef」两个子字符串。「bcdef」比「abcdef」短一个字符，理论上也稍微容易点。假设我们有这样的函数能接受一个字符串，然后像变戏法一样就能返回一个翻转后的字符串。

如下奉上C#代码，更容易去体会。

 private int intNumber = 1;
        //循环到字符串最短长度
        private int intMinLength = 0;
        private void button1_Click(object sender, EventArgs e)
        {

            //txtStart 文件框 输入初始值如：abcbef。
            //txtCount 文件框 输入循环的次数。
            string strStart = txtStart.Text.Trim();
            string strCount = txtCount.Text.Trim();
            
            if (string.IsNullOrEmpty(strStart))
            {
                MessageBox.Show("初始值不可以为空");
            }
            else if (string.IsNullOrEmpty(strCount))
            {
                MessageBox.Show("循环次数不可以为空");
            }
            else if (strStart.Length <= int.Parse(strCount))
            {
                MessageBox.Show("次数必须小于初始字符串长度");
            }
            else
            {
                //字符串长度 减去 要循环的次数 得到 循环到字符串最短长度（每次少一个）
                intMinLength = strStart.Length - int.Parse(strCount);
                //一个lab，显示结果
                label1.Text = "初始值为：" + strStart + "\r\n\r\n";
                intNumber = 1;
                string strReturnVal = revertString(strStart);
                label1.Text =   label1.Text + "\r\n最终值：" + strReturnVal;
                //MessageBox.Show(strReturnVal);
            }
           

        }

        /// <summary>
        /// 本递归把一个字符串，全翻转过来。 如将abcdef转为fedcba
        /// </summary>
        /// <param name="str">初始值</param>
        /// <returns></returns>
        protected string revertString(string str)
        {
            //循环次数
            int intCount = int.Parse(txtCount.Text.Trim());
            if (str.Length <= intMinLength)
            {
                return str;
            }
            label1.Text = label1.Text + "第" + intNumber + "次：" + str.Substring(1) + str.Substring(0, 1) + "\r\n";
            intNumber++;
            return revertString(str.Substring(1)) + str.Substring(0,1);

        }