JS实现图的创建和遍历

图分为无向图和有向图 

图的存储结构有邻接矩阵、邻接表、十字链表、邻接多重表这四种，最常用的是前两种

本篇主要是利用邻接矩阵实现无向图的创建和遍历（深度优先、广度优先），深度优先其实就是二叉树里的前序遍历

 

  

 

 

利用邻接矩阵（边数组）创建图

let scanf = require('scanf');
//定义邻接矩阵
let Arr2 = [
    [0, 1, 0, 0, 0, 1, 0, 0, 0],
    [1, 0, 1, 0, 0, 0, 1, 0, 1],
    [0, 1, 0, 1, 0, 0, 0, 0, 1],
    [0, 0, 1, 0, 1, 0, 1, 1, 1],
    [0, 0, 0, 1, 0, 1, 0, 1, 0],
    [1, 0, 0, 0, 0, 0, 1, 0, 0],
    [0, 1, 0, 1, 0, 1, 0, 1, 0],
    [0, 0, 0, 1, 1, 0, 1, 0, 0],
    [0, 1, 1, 1, 0, 0, 0, 0, 0],
]

let numVertexes = 9, //定义顶点数
    numEdges = 14; //定义边数

// 定义图结构  
function MGraph() {
    this.vexs = []; //顶点表
    this.arc = []; // 邻接矩阵，可看作边表
    this.numVertexes = null; //图中当前的顶点数
    this.numEdges = null; //图中当前的边数
}
let G = new MGraph(); //创建图使用

//创建图
function createMGraph() {
    G.numVertexes = numVertexes; //设置顶点数
    G.numEdges = numEdges; //设置边数

    //录入顶点信息
    for (let i = 0; i < G.numVertexes; i++) {
        G.vexs[i] = scanf('%s'); //String.fromCharCode(i + 65); ascii码转字符
    }
    console.log(G.vexs) //打印顶点

    //邻接矩阵初始化
    for (let i = 0; i < G.numVertexes; i++) {
        G.arc[i] = [];
        for (j = 0; j < G.numVertexes; j++) {
            G.arc[i][j] = Arr2[i][j]; //INFINITY; 
        }
    }

    /**以下是手动录入的方式 */
    // for (let k = 0; k < G.numEdges; k++) {
    //     console.log('输入边（vi,vj）上的下标i,下标j和权w:');
    //     let rlt = scanf('%d,%d,%d');
    //     let i = rlt[0], j = rlt[1], w = rlt[2];
    //     G.arc[i][j] = w;
    //     G.arc[j][i] = G.arc[i][j]; //无向图，矩阵对称
    // }

    console.log(G.arc); //打印邻接矩阵
}

深度优先遍历

let visited = []; //访问标志数组，遍历时使用

//邻接矩阵的深度优先递归算法
function DFS(i) {
    visited[i] = true;
    console.log('打印顶点:', G.vexs[i]) //打印顶点 ,也可以其他操作
    for (let j = 0; j < G.numVertexes; j++) {
        if (G.arc[i][j] == 1 && !visited[j]) {
            console.log(G.vexs[i], '->', G.vexs[j])
            DFS(j) //对未访问的顶点进行递归
        }
    }
}
//邻接矩阵的深度遍历操作
function DFSTraverse() {
    for (let i = 0; i < G.numVertexes; i++) {
        visited[i] = false;
    }
    for (let i = 0; i < G.numVertexes; i++) {
        if (!visited[i])
            DFS(i)
    }
}

广度优先遍历

//邻接矩阵的广度遍历算法
function BFSTraverse() {
    let queue = []; //初始化队列
    for (let i = 0; i < G.numVertexes; i++) {
        visited[i] = false;
    }
    for (let i = 0; i < G.numVertexes; i++) { //对每一个顶点做循环
        if (!visited[i]) { //如果没有访问过就处理
            visited[i] = true;
            console.log('打印顶点：', G.vexs[i]) //也可以是其他操作
            queue.push(i); //将此顶点入队列
            while (queue.length != 0) { //当前队列不为空
                queue.shift();
                for (let j = 0; j < G.numVertexes; j++) {
                    //判断其他顶点若与当前顶点存在边且未访问过
                    if (G.arc[i][j] == 1 && !visited[j]) {
                        visited[j] = true;
                        console.log(G.vexs[i], '->', G.vexs[j])
                        console.log('打印顶点：', G.vexs[j])
                        queue.push(j) //将此顶点放入队列
                    }
                }
            }
        }
    }
}

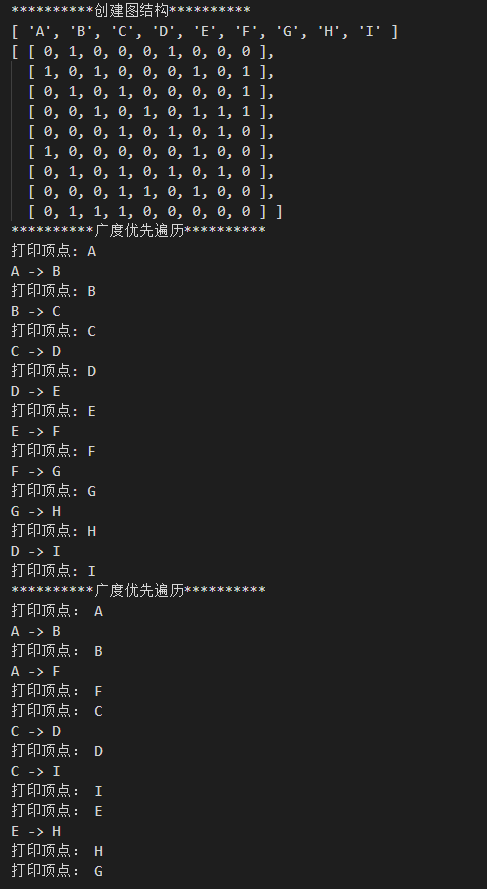
运行：

console.log('**********创建图结构**********');

createMGraph();

console.log('**********广度优先遍历**********');

DFSTraverse();

console.log('**********广度优先遍历**********');

BFSTraverse();

结果：