栈的应用

POJ2559http://poj.org/problem?id=2559

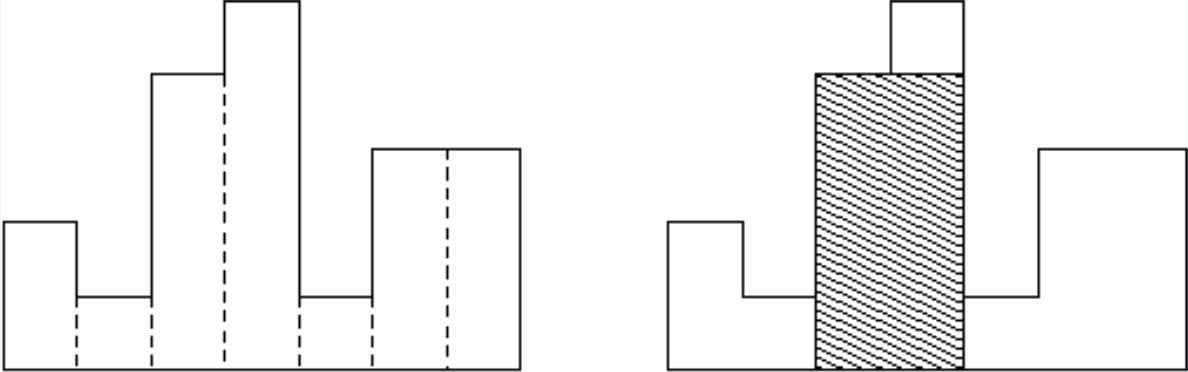
求一系列不等高的柱状体中最大的长方形面积

思路：答案中的长方形必定有至少有一条边与其中一个柱状体的顶边重合。那么我们只需求解对于每个柱状体，它最多能向左右延伸多长。

设当前柱状体下标为j (0 <= j < n)

L[i] = (j <= i 且 h[j - 1] < h[i]的最大的j)（左闭）

R[i] = (j > i 并且h[j] > h[i]的最小的j)（右开）

ans = max{h[i] * (R[i] - L[i])}

 

在计算L[i]时，若柱状体左端高度高于其，则其左端的所有柱状体高度没有意义。

运用栈，栈中的元素从上到下的值为x[i], 则x[i] > x[i + 1] 且h[x[i]] > h[x[i + 1]]

 在计算L[i]时，首先，当栈顶的元素j满足h[j] >= h[i], 则不断取出栈顶元素。

如栈的为空，则L[i] = 0; 若h[j] < h[i], 则L[i] = j + 1。然后把i压入栈中。

 

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <vector>
#define INF 0x3f3f3f3f
#define mod 1000000007
typedef long long LL;
using namespace std;

const int maxn = 100000 + 10;
int hei[maxn];
int s[maxn], l[maxn], r[maxn];

int N;
LL ans;

int main(int argc, const char * argv[]) {
    while (~scanf("%d", &N) && N) {
        memset(hei, 0, sizeof(hei));
        memset(l, 0, sizeof(l));
        memset(r, 0, sizeof(r));
        for (int i = 0; i < N; i++) {
            scanf("%d", &hei[i]);
        }
        int t = 0;
        for (int i = 0; i < N; i++) {
            while (t > 0 && hei[s[t - 1]] >= hei[i]) t--;
            if (t == 0) {
                l[i] = 0;
            } else {
                l[i] = s[t - 1] + 1;
            }
            s[t++] = i;
        }
        t = 0;
        for (int i = N - 1; i >= 0; i--) {
            while (t > 0 && hei[s[t - 1]] >= hei[i]) t--;
            if (t == 0) {
                r[i] = N;
            } else {
                r[i] = s[t - 1];
            }
            s[t++] = i;
        }
        
        ans = -1;
        for (int i = 0; i < N; i++) {
            LL tmp = (LL)hei[i] * (LL)(r[i] - l[i]);
            ans = max(ans, tmp);
        }
        printf("%lld\n", ans);
        
    }
    return 0;
}