python——算法(时间复杂度,空间复杂度,二分查找,排序们)
算法(Algorithm)概念:一个计算过程,解决问题的方法
递归的两大特点: 1、自己调用自己 2、有穷性(python默认只能递归999次)自己修改递归深度:sys.setrecursionlimit(100000)
def func1(x):
if x>0:
print(x)
func1(x-1)
def func2(x):
if x>0:
func2(x-1)
print(x) # 当递归完了以后,才输出
func1(5)
>> 5,4,3,2,1
func2(5)
>> 1,2,3,4,5 # 就是他从递归中出来了,做他该做的事
时间复杂度
代码 时间复杂度
print('Hello World') O(1)
for i in range(n): O(n)
print('Hello World')
for i in range(n):
for j in range(n): O(n^2)
print('Hello World')
for i in range(n):
for j in range(n): O(n^3)
for k in range(n):
print('Hello World')
while n > 1:
print(n) O(logn)
n = n // 2
while n > 1:
print(n) O(n)
n = n - 1
时间复杂度是一个估计的时间(正常人都说这个活还有几个月就完成了,没有说几个月零几天完成)
O(1)==>几小时
O(n)==>几天
O(n^2)==>几个月
O(n^3)==>几年
时间复杂度小结
时间复杂度是用来估计算法运行时间的一个式子(单位)。
一般来说,时间复杂度高的算法比复杂度低的算法慢。
常见的时间复杂度(按效率排序)
O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n2logn)<O(n3)
不常见的时间复杂度(看看就好)
O(n!) O(2n) O(nn) …
如何一眼判断时间复杂度?
循环减半的过程 o(logn)
几次循环就是n的几次方的复杂度
空间复杂度
用来评估算法内存占用大小的一个式子
a,b,c单独调用几个变量 o(1) [] 一维列表 o(n) [[],[],...] 二维列表 o(n^2) [[[],[],...],...] 一维列表 o(n^3)
列表查找方法:(从列表中查找指定元素)
顺序查找
def search(list,value): for i in list: if i == value: return i else: return 你查找的值列表中不存在
二分查找
@cal_time
def bin_search(data_set,val):
low = 0
high = len(data_set)-1
while low <= high:
mid = (low+high)//2 # 整除2
if data_set[mid] == val: # 如果等于要查找的值,返回下标
return mid
elif data_set[mid] < val: # 如果列表中间的值小于需要的值
low = mid + 1 # 则把最小的下标改成mid+1
else: # 如果列表中间的值大于需要的值
high = mid - 1 # 则把最大的下标改成mid-1
return # 如果没找到return空

1 import random,time 2 3 def cal_time(func): # 装饰器(不能加在递归函数上) 4 def index(*args,**kwargs): 5 t1 = time.time() 6 result = func(*args,**kwargs) 7 t2 = time.time() 8 print("%s running time: %s secs." % (func.__name__, t2 - t1)) 9 return result 10 return index 11 12 @cal_time 13 def bin_search(data_set,val): 14 low = 0 15 high = len(data_set)-1 16 while low <= high: 17 mid = (low+high)//2 # 整除2 18 if data_set[mid]['id'] == val: # 如果等于要查找的值,返回下标 19 return mid 20 elif data_set[mid]['id'] < val: # 如果列表中间的值小于需要的值 21 low = mid + 1 # 则把最小的下标改成mid+1 22 else: # 如果列表中间的值大于需要的值 23 high = mid - 1 # 则把最大的下标改成mid-1 24 return # 如果没找到return空 25 26 def random_list(n): # 生成的列表长度 27 result = [] 28 ids = list(range(1001,1001+n)) # list(生成器) 29 a1 = ['赵','钱','孙'] 30 a2 = ['级', '震', '宇'] 31 a3 = ['伯','仲','叔','季'] 32 for i in range(n): 33 age = random.randint(18,66) 34 id = ids[i] 35 name = random.choice(a1)+random.choice(a2)+random.choice(a3) 36 dic = {'id':id,'name':name,'age':age} 37 result.append(dic) 38 return result 39 40 41 data_set = random_list(500) 42 code = bin_search(data_set,1450) 43 print(code)
列表排序:
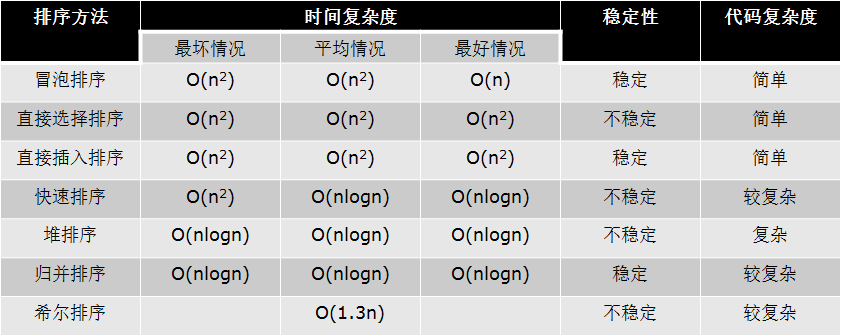
low B三人组(时间复杂度都是O(n^2))
a.冒泡排序 ***(优化后最好是O(n) 已经是顺序的情况下)
列表每两个相邻的数,如果前边的比后边的大,那么交换这两个数……
# 冒泡排序1
@cal_time
def bubble_sort(li):
for i in range(len(li)-1):
for j in range(len(li)-i-1):
if li[j] > li[j+1]:
li[j],li[j+1] = li[j+1],li[j]
return li
# 冒泡排序2,优化后的,当上一趟没有发生交换,默认已经排好了,不再进行排序
@cal_time
def bubble_sort2(li):
for i in range(len(li)-1):
exchange = False
for j in range(len(li)-i-1):
if li[j] > li[j+1]:
li[j],li[j+1] = li[j+1],li[j]
exchange = True
if not exchange:
break
return li
data = list(range(10000))
random.shuffle(data)
bubble_sort(data),bubble_sort2(data)
b.选择排序
一趟遍历记录最小的数,放到第一个位置;
下一趟再遍历记录剩余列表中最小的数,继续放置...
def select_sort(li):
for i in range(len(li) - 1):
for j in range(i+1,len(li)):
if li[j] < li[i]:
li[i], li[j] = li[j], li[i]
c.插入排序
列表被分为有序区和无序区两个部分。最初有序区只有一个元素。
每次从无序区选择一个元素,插入到有序区的位置,直到无序区变空。
def insert_sort(li):
for i in range(1, len(li)):
tmp = li[i]
j = i - 1
while j >= 0 and li[j] > tmp:
li[j+1]=li[j]
j = j - 1
li[j + 1] = tmp
高级算法 ***(一般情况下,时间复杂度都是O(nlogn))
a.快速排序(时间复杂度 最好情况:O(nlogn),一般情况:O(nlogn),最坏:O(n^2))
取一个元素p(第一个元素),使元素p归位;
列表被p分成两部分,左边都比p小,右边都比p大;
递归完成排序。
算法关键点:
- 整理
- 递归
口诀:跟着我右手左手一个慢动作右手左手慢动作重播(递归)
def quick_sort_x(data, left, right):
if left < right:
mid = partition(data, left, right)
quick_sort_x(data, left, mid - 1) # 递归
quick_sort_x(data, mid + 1, right)
def partition(data, left, right):
tmp = data[left]
while left < right:
while left < right and data[right] >= tmp:
right -= 1
data[left] = data[right]
while left < right and data[left] <= tmp:
left += 1
data[right] = data[left]
data[left] = tmp
return left
@cal_time # 不能直接在递归函数上套装饰器,所以要另写一个函数调用他
def quick_sort(data):
return quick_sort_x(data, 0, len(data) - 1)
平时还是用系统自带的(用C语言写的,比快排还快)
def sys_sort(data):
return data.sort()
修改递归深度:sys.setrecursionlimit(100000)
b.堆排序
树:
树是一种数据结构 比如:目录结构
树是一种可以递归定义的数据结构
树是由n个结点组成的集合:
- 如果n=0,那这是一棵空树;
- 如果n>0,那存在1个节点作为树的根节点,其他节点可以分为m个集合,每个集合本身又是一棵树。
一些概念
根结点、叶子结点
- 叶子结点:没有分支的节点(度为0)
树的深度(高度):树有几层
树的度
- 度:一个结点拥有的子树数(有几个分支)
- 树的度:树内各结点的度的最大值(树里最大的度)
孩子结点/父结点
子树:孩子结点又分成了一颗树
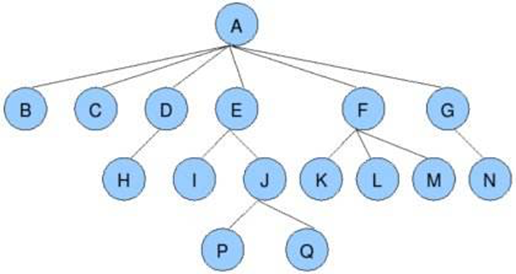
二叉树:度不超过2的树(每个节点最多有两个叉)
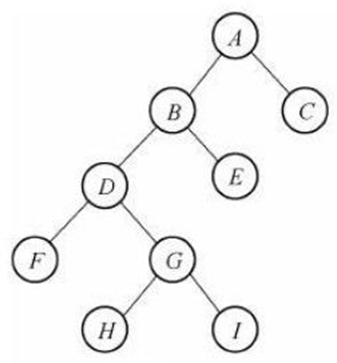
两种特殊的二叉树
a、满二叉树(二叉树一个都不少,满的)
b、完全二叉树(满二叉树从后面减少结点)
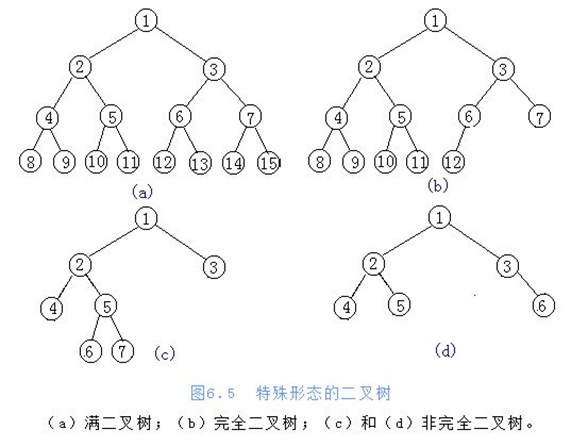
完全二叉树的储存方式
a、链式存储方式
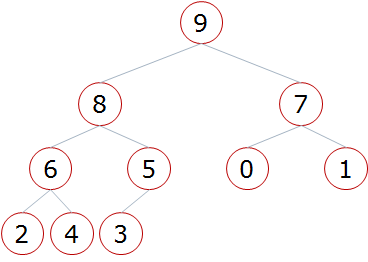
b、顺序存储方式(列表)
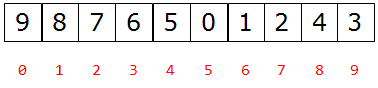
父节点和左孩子节点的编号下标之间的关系:i => 2i+1
0~1 1~3 2~5 3~7 4~9
父节点和右孩子节点的编号下标之间的关系:i => 2i+2
0~2 1~4 2~6 3~8 4~10
主角来了:堆排序
堆排序过程(思路)
1、建立堆
2、得到堆顶元素,为最大元素
3、去掉堆顶,将堆最后一个元素放到堆顶,此时可通过一次调整重新使堆有序。
4、堆顶元素为第二大元素。
5、重复步骤3,直到堆变空。
def sift(data, low, high):
i = low # 最高位置的领导(不称职)位置编号:0
j = 2 * i + 1 # 找他的儿子看能不能当 位置编号:1
tmp = data[i] # 把最高位的领导撸下来
while j <= high: # 只要没到子树的最后
if j < high and data[j] < data[j + 1]: # 如果下一位比他值大则j+1,因为是二叉树不用考虑第1位比第2位大,比第3位小的情况
j += 1
if tmp < data[j]: # 如果领导不能干
data[i] = data[j] # 小领导上位
i = j # j的位置空出来了,接着找他的儿子能接替他的位置 假设 位置编号:1
j = 2 * i + 1 # 位置编号:3
else: # 省长,县长,...都选好了,跳出循环
break
data[i] = tmp # 在循环结束后都会空出一个位置,把之前的那个不称职的最高位的领导放进去
@cal_time
def heap_sort(data):
n = len(data)
for i in range(n // 2 - 1, -1, -1):
sift(data, i, n - 1)
#堆建好了
for i in range(n-1, -1, -1): #i指向堆的最后
data[0], data[i] = data[i], data[0] #领导退休,***民上位
sift(data, 0, i - 1) #调整出新领导
c.归并排序
一次归并代码
def merge(li, low, mid, high): # 假设以mid为分界线,左右两边都是有序排列的
i = low # 有序的左边的起始位置
j = mid + 1 # 分界线的位置+1 ==> 另一边的起始位置
ltmp = [] # 新建一个空列表
while i <= mid and j <= high: # 左边小于等于mid,右边小于等于high
if li[i] < li[j]: # 如果左边值小于右边
ltmp.append(li[i]) # 把左边值加进新列表中
i += 1 # i的位置前进一格
else: # 如果左边值大于右边
ltmp.append(li[j]) # 把右边的值加进新列表中
j += 1 # j的位置前进一格
while i <= mid: # 如果右边没值了
ltmp.append(li[i]) # 把左边的值全都加进新列表中
i += 1
while j <= high:
ltmp.append(li[j])
j += 1
li[low:high+1] = ltmp # 把新列表赋值给旧的列表
归并排序的思路
分解:将列表越分越小,直至分成一个元素。一个元素是有序的。
[] ==> 单个元素
合并:将两个有序列表归并,列表越来越大。
将两个表以归并的方式组合到一起,就变成有序的了
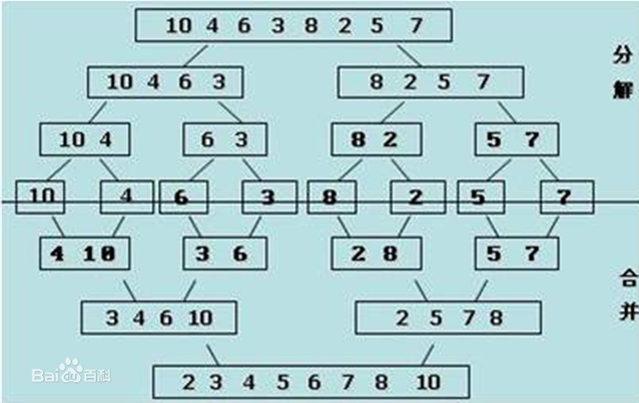
def _mergesort(li, low, high):
if low < high:
mid = (low + high) // 2
_mergesort(li,low, mid) # 递归
_mergesort(li, mid+1, high)
merge(li, low, mid, high)
@cal_time
def mergesort(li):
_mergesort(li, 0, len(li) - 1)
小结
一般情况下,就运行时间而言:
快速排序 < 归并排序 < 堆排序
三种排序算法的缺点:
快速排序:极端情况下排序效率低
归并排序:需要额外的内存开销
堆排序:在快的排序算法中相对较慢
不常用排序
希尔排序
思路
希尔排序是一种分组插入排序算法。
首先取一个整数d1=n/2,将元素分为d1个组,每组相邻量元素之间距离为d1,在各组内进行直接插入排序;
取第二个整数d2=d1/2,重复上述分组排序过程,直到di=1,即所有元素在同一组内进行直接插入排序。
希尔排序每趟并不使某些元素有序,而是使整体数据越来越接近有序;最后一趟排序使得所有数据有序。
def shell_sort(li):
gap = int(len(li) // 2)
while gap >= 1:
for i in range(gap, len(li)):
tmp = li[i]
j = i - gap
while j >= 0 and tmp < li[j]:
li[j + gap] = li[j]
j -= gap
li[i - gap] = tmp
gap = gap // 2
排序小结
练习:
1、现在有一个列表,列表中的数范围都在0到100之间,列表长度大约为100万。设计算法在O(n)时间复杂度内将列表进行排序。
# 计数排序:创建一个列表,用来统计每个数出现的次数。
def count_sort(li, max_num):
count = [0 for i in range(max_num + 1)] # 创建一个指定长度的列表 [0,0,0,...]
for num in li:
count[num] += 1 # 找到自己建的列表中相应的下标,让他的内容+1
i = 0
for num,m in enumerate(count): # num是编号,m是内容
for j in range(m):
li[i] = num
i += 1
2、现在有n个数(n>10000),设计算法,按大小顺序得到前10大的数。(欠)
应用场景:榜单TOP 10



