神经网络的正向和反向传播

本文目的：

以自己的理解，大致介绍神经网络，并梳理神经网络的正向和反向传播公式。

神经网络简介

神经网络是机器学习的分支之一，因为大量数据的出现和可供使用以及神经网络因深度和广度的增加对于大量数据的可扩展性，目前神经网络逐渐变成了除常规机器学习方法外的另一个主流。人们所认识的神经网络一般为Fig. 1所示：

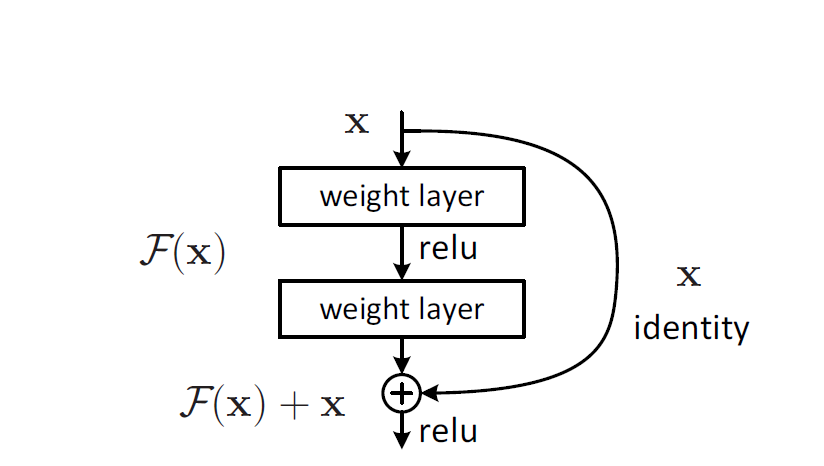Fig. 1 基本神经网络结构图 神经网络的结构图由三部分组成，分别是输入层、输出层以及隐藏层。对于一个神经网络来讲，层次的结构并不单纯是这样简单的，目前还有很多种神经网络的结构，包括不限于卷积神经网络、循环神经网络和残差网络等。 卷积神经网络结构图 循环神经网络结构图 残差网络结构图 神经网络并不单纯地是基础我们常见的神经网络，因此不要好高骛远认为自己什么都懂了。神经网络虽然种类很多并且该学的也很多，但同时也不能着急想一口气吃个胖子，慢慢来。

前向传播和反向传播

说起典型的神经网络的分析，那么就不得不提到前向传播和反向传播。前向传播使得输入可以通过神经网络得到输出，输出和真实值可以反向矫正神经网络的参数，使得得到一个适合具体问题的神经网络。

前向传播

Fig. 2 典型神经网络 从Fig. 2可以看到，一个典型的神经网络一般由输入层，隐藏层和输出层组成。而每层与层直接的连线，实际上是一个数学运算，运算的系数的整体称为神经网络的参数$\theta$，它其中包含了乘法运算$W$和线性叠加$b$。经过运算我们可以算出隐藏层中间矢量$\vec{z} = [a_4\,a_5\,a_6\,a_7]^T$与输入$X = [x_1\,x_2\,x_3]^T$的关系： \begin{equation} \vec{z} = W^TX + b \end{equation} 或： \begin{equation} \vec{z} = \theta X \end{equation} 如图Fig. 3， 当隐藏层很多的时候，我们用参数$W^{[l]}$和$b^{[l]}$来表示是第几层的参数，因此一般来说中间量$\vec{z}^{[l]}$与前一项$\vec{a}^{[l-1]}$的关系为： \begin{equation} \vec{z}^{[l]} = W^{[l]T}\vec{a}^{[l-1]} + b^{[l]} \end{equation} 而为什么我们叫$\vec{z}^{(l)}$为中间量，并且什么是$\vec{a}$呢？其实在神经网络里面，每一个圆圈不仅是一个线性的运算，还包含了一个非线性的预算，这个非线性的运算我们可以叫它激励函数用$g()$来表示。如果没有涉及这个非线性运算的话，那么无论是多深多广的神经网络都可以用一个神经元来替代了（请自行证明），因此神经网络的正向传播公式为： \begin{equation} \vec{z}^{[l]} = W^{[l]T}\vec{a}^{[l-1]} + b^{[l]} \end{equation} \begin{equation} \vec{a}^{[l]} = g(\vec{z}^{[l]}) \end{equation} Fig. 3 多层神经网络 ####反向传播 反向传播是矫正神经网络参数的步骤，同时反向传播在典型神经网络里也是一个比较容易出错的知识点。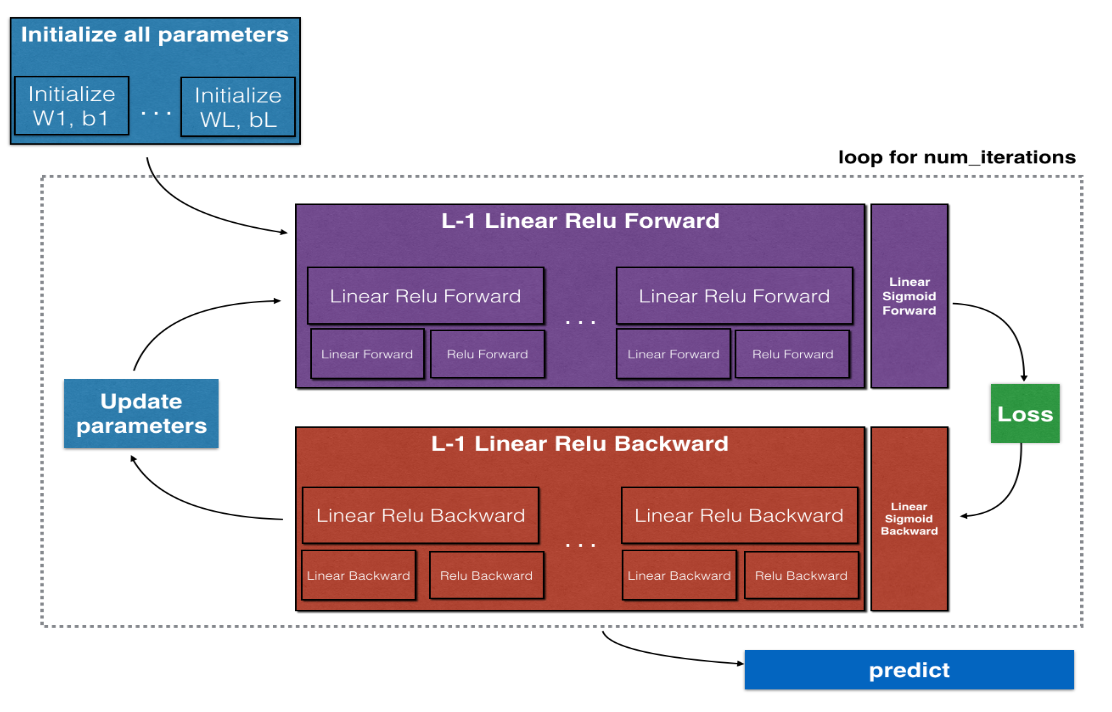 Fig. 4 正向反向传播示意图 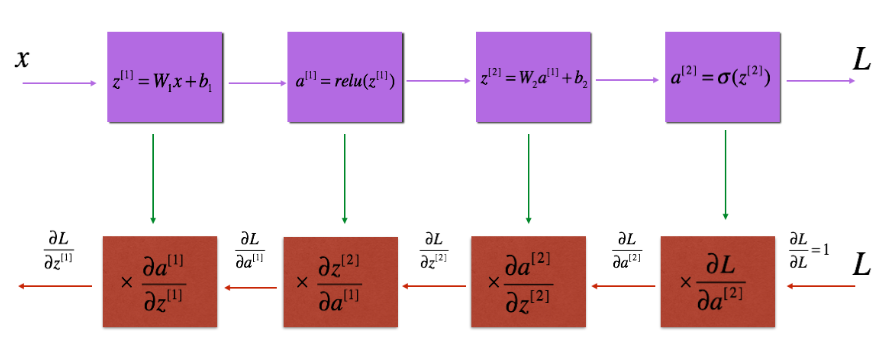#####Loss函数 由Fig.4 可见，我们已经完成了正向传播，即已知输入和参数后算出输出层的值。但是想计算反向传播，我们还需要定义Loss函数也就是常说的交叉熵： \begin{equation} -(ylog(a^{[L]}) + (1-y)log(1- a^{[L]})) \end{equation} 但是以上仅是对于一个数据来说的Loss函数，对于多个数据的Loss函数来说我们定义$y^{(i)}$表示其第i个数据，一共m个数据的Loss函数为： \begin{equation} -\frac{1}{m} \sum\limits_{i = 1}^{m} (y^{(i)}\log\left(a^{[L] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[L] (i)}\right)) \end{equation} #####矢量化 完成了Loss函数的定义之后，让我们深入看Fig. 5用以了解反向传播的公式： Fig. 5 反向传播 我们的目标是求得$\frac{\partial L}{\partial W^{[l]}}$和$\frac{\partial L}{\partial b^{[l]}}$。由正向传播公式$\vec{Z}^{[l]} = W^{[l]T}\vec{A}^{[l-1]} + b^{[l]}$得知，$\frac{\partial L}{\partial b^{[l]}}$ = $\frac{1}{m} \sum_{i = 1}^{m} dZ^{[l](i)}$，$\frac{\partial L}{\partial W^{[l]}}$ = $\frac{1}{m}\frac{\partial L}{\partial Z^{[l]}}A^{[l-1]T}$。通过以上公式发现两个疑惑点，为什么之前公式里的$z$变成了$Z$，同时$a$，变成了$A$呢？并且，$\frac{1}{m}$又是何来呢？ 首先解释$a,z$和$A,Z$的问题： 当我们计算Loss函数的时候我们意识到，我们不仅是有一个数据，我们会有很多很多的数据用来优化神经网络的参数。使用多个数据有两个办法： 1. 使用循环： 但是使用循环有一个缺陷就在于数据太大的时候会大大降低运行时间 2. 矢量化： 将数据全部矢量化，使得去除循环。

矢量化详解

从输入\(X\)开始，我们的每个输入\(X\)都有很多特征\(X = [x_1\,x_2\,x_3\,...\,x_n]^T\)而我们也会有很多的输入，我们组成新的输入\(X = [X^{(1)}\,X^{(2)}\,...\,X^{(m)}]\)，因此\(X\)包含了所有的数据，每一列是一个数据，每个数据包含n个特征，一共有m个数据。因此\(Z = [z^{(1)}\,z^{(2)}\,...\,z^{(m)}]\)，\(A = [a^{(1)}\,a^{(2)}\,...\,a^{(m)}]\)由此我们完成了矢量化。尽管使用了矢量化，正向传播的公式也没有变，\(b^{[l]}\)也可以通过python的广播来完成：
\begin{equation}
\vec{A}^{[l]} = W^{{[l]T}\vec{A}} + b^{[l]}
\end{equation}
\begin{equation}
\vec{A}^{[l]} = g(\vec{Z}^{[l]})
\end{equation}
但是，因为参数\(W\in R^{l \times l-1}\)和\(b \in R^l\)的维度没有变化，当使用反向传播计算\(\frac{\partial L}{\partial W^{[l]}}\)和\(\frac{\partial L}{\partial b^{[l]}}\)的时候，我们需要乘\(\frac{1}{m}\)：
\(\frac{\partial L}{\partial Z^{[l]}}A^{[l-1]T} = [dz^{[l](1)}\,...\,dz^{[l](m)}][a^{[l-1](1)}\,...\,a^{[l-1](m)}]^T\)
\(\frac{\partial L}{\partial Z^{[l]}}A^{[l-1]T} = dz^{[l](1)}a^{[l-1](1)} + ... +dz^{[l](m)}a^{[l-1](m)} = m\frac{\partial L}{\partial W^{[l]}}\)
同理，
\(\frac{\partial L}{\partial Z^{[l]}} = [dz^{[l](1)}\,...\,dz^{[l](m)}]\)
\(\frac{\partial L}{\partial b^{[l]}} = \frac{1}{m} \sum_{i = 1}^{m} dZ^{[l](i)}\)

反向传播公式

目前我们得到了：\(\frac{\partial L}{\partial b^{[l]}}\) = \(\frac{1}{m} \sum_{i = 1}^{m} dZ^{[l](i)}\)，\(\frac{\partial L}{\partial W^{[l]}}\) = \(\frac{1}{m}\frac{\partial L}{\partial Z^{[l]}}A^{[l-1]T}\)（为什么\(A^{[l-1]}是要转置的呢？\)），但是为了计算\(\frac{\partial L}{\partial W^{[l]}}\)和\(\frac{\partial L}{\partial b^{[l]}}\)，我们还需要求得\(\frac{\partial L}{\partial Z^{[l]}}\)。
正向传播公式：\(A^{[l]} = g(Z^{[l]})\)，\(\vec{Z}^{[l]} = W^{[l]T}\vec{A}^{[l-1]} + b^{[l]}\)
\begin{equation}
dA^{[L]} = \frac{\partial loss}{\partial A^{[L]}}
\end{equation}
\begin{equation}
dZ^{[l]} = dA^{{[l]}\dot{g(Z})}
\end{equation}
\begin{equation}
dA^{[l-1]} = W^{[l]T}dZ
\end{equation}
\begin{equation}
\frac{\partial L}{\partial W^{[l]}} = \frac{1}{m}\frac{\partial L}{\partial Z^{[l]}}A
\end{equation}
\begin{equation}
\frac{\partial L}{\partial b^{[l]}} = \frac{1}{m} \sum_{i = 1}^{m} dZ^{[l] (i)}
\end{equation}