第九节 线性无关、基和维数

第九节 线性无关、基和维数

线性无关

在前几节提到过，矩阵\(A\)为\(m \times n\)矩阵，其中\(m<n\)（也就是\(Ax=b\)中未知数个数多于方程数）。则\(A\)中具有至少一个自由变量，那么\(Ax=b\)一定具有非零解，此时\(A\)的列变量是线性相关的

1. 假设\({c\mathop{{}}\nolimits_{{1}}v\mathop{{}}\nolimits_{{1}}+c\mathop{{}}\nolimits_{{2}}v\mathop{{}}\nolimits_{{2}}+\text{ … }+c\mathop{{}}\nolimits_{{k}}v\mathop{{}}\nolimits_{{k}}=0}\)且只有在\({c\mathop{{}}\nolimits_{{1}}=c\mathop{{}}\nolimits_{{2}}=\text{ … }=c\mathop{{}}\nolimits_{{k}}=0}\)时成立，那么向量\({v\mathop{{}}\nolimits_{{1}},v\mathop{{}}\nolimits_{{2}},\text{ … },v\mathop{{}}\nolimits_{{k}}}\)是线性无关的。如果任何不为零，那么这些向量是线性相关的

2. 如果矩阵\(A\)的列向量是线性无关的，则\(A\)的所有列均为主元列，没有自由列，矩阵的秩为\(n\)。如果\(A\)的列向量线性相关，则矩阵的秩小于\(n\)，并且存在自由列

3. 当一个空间是由向量\({v\mathop{{}}\nolimits_{{1}},v\mathop{{}}\nolimits_{{2}},\text{ … },v\mathop{{}}\nolimits_{{k}}}\)的所有线性组合组成时，我们称这些向量张成了这个空间。比如矩阵的列向量张成了该矩阵的列空间。而张成的空间\(S\)，就是包含这些向量的最小空间

向量空间的基

1. 向量空间的基是具有如下性质的一组向量：

• 这组向量是线性无关的
• 这组向量张成了向量空间

2. 判断一组向量是否能构成“基”的一个简单方法是：把它们做成一个矩阵， 消元， 看是否存在自由变量；如果存在自由变量， 不是空间的一组“基”
3. 对于\(n\)个向量组成的\(n \times n\)方阵，如果方阵是可逆的，那么它就能构成它的“基”

向量空间的维数

1. 基向量的个数称为空间的维数
2. 一个空间的基可能有很多个，拿\({R\mathop{{}}\nolimits^{{3}}}\)空间举例，某可逆\(3 \times 3\)矩阵，它的列都是\({R\mathop{{}}\nolimits^{{3}}}\)的基，但不管有多少组基，所有这些基都有共同点，那就是其中向量的个数都是一定的，如果是\({R\mathop{{}}\nolimits^{{3}}}\)空间，那么基向量的个数就是3，如果是\({R\mathop{{}}\nolimits^{{n}}}\)空间，那么基向量的个数就是n

比如：向量\({ \left[ {{\left. \begin{array}{*{20}{l}} {1}\\ {1}\\ {2} \end{array} \right] }}\right. },{ \left[ {{\left. \begin{array}{*{20}{l}} {2}\\ {2}\\ {5} \end{array} \right] }}\right. }\)可以张成\({R\mathop{{}}\nolimits^{{3}}}\)中的一个平面，但无法构成一组基

列空间和零空间的基

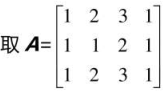
1. 列空间

   1. 后两列与前两列是线性相关的，而前两列之间线性无关。故前两列为主元列，它们组成了列空间\(C(A)\)的一组基，该矩阵的秩为2

   2. 所以对于任意矩阵均有：

      矩阵的秩\(r\)=矩阵主元列个数=列空间的维数

2. 零空间

   1. 刚才分析可知，后两列是自由列。所以对自由变量进行赋值：

      • \({x\mathop{{}}\nolimits_{{3}}=1,x\mathop{{}}\nolimits_{{4}}=0}\)，得到\({ \left[ {{\left. \begin{array}{*{20}{l}} {\text{ }-1}\\ {\text{ }-1}\\ {\text{ }\text{ }0}\\ {\text{ }\text{ }1} \end{array} \right] }}\right. }\)
      • \({x\mathop{{}}\nolimits_{{3}}=0,x\mathop{{}}\nolimits_{{4}}=1}\)，得到\({ \left[ {{\left. \begin{array}{*{20}{l}} {1}\\ {0}\\ {0}\\ {1} \end{array} \right] }}\right. }\)

      除了零向量外这两个特解也在\(N(A)\)内

   2. 所以对于零空间：

      零空间的维数=自由列的个数=\(n-r\)

      上例中，求得的两个特解就是零空间的一组基