第七节 求Ax=0的主变量、特解

第七节 求Ax=0的主变量、特解

矩阵的秩

取矩阵\(A\)为\({ \left[ {{\left. \begin{array}{*{20}{l}} {1\text{ }\text{ }2\text{ }\text{ }2\text{ }\text{ }2}\\ {2\text{ }\text{ }4\text{ }\text{ }6\text{ }\text{ }8}\\ {3\text{ }\text{ }6\text{ }\text{ }8\text{ }10} \end{array} \right] }}\right. }\)

消元得到: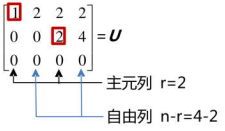

1. 矩阵\(U\)为梯形矩阵,第三行为0的原因是矩阵\(A\)第三行是前两行相加（线性组合）而成

2. 矩阵的秩（rank）就是矩阵的主元个数，比如矩阵\(U\)的秩为2。矩阵包含主元的列称为主元列（pivot column），不包含主元的列称为自由列（free column）

特解

第一节就已提到，解线性方程先消元再回代，解\(Ax=0\)，在消元后变为\(Ux=0\)，即

在上例中,有两列主元列两列自由列，对自由变量进行赋值，比如令\({x\mathop{{}}\nolimits_{{2}}=1,x\mathop{{}}\nolimits_{{4}}=0}\)，回代方程组中得：\({ \left\{ \begin{array}{*{20}{l}} {x\mathop{{}}\nolimits_{{1}}+2x\mathop{{}}\nolimits_{{2}}+2x\mathop{{}}\nolimits_{{3}}+2x\mathop{{}}\nolimits_{{4}}=0}\\ {2x\mathop{{}}\nolimits_{{3}}+4x\mathop{{}}\nolimits_{{4}}=0} \end{array}\right. } \Rightarrow { \left\{ \begin{array}{*{20}{l}} {x\mathop{{}}\nolimits_{{1}}=-1}\\ {x\mathop{{}}\nolimits_{{3}}=0} \end{array}\right. }\)

即特解为\({x={ \left[ {{\left. \begin{array}{*{20}{l}} {-2}\\ {\text{ }1}\\ {\text{ }0}\\ {\text{ }0} \end{array} \right] }}\right. }}\)

再令自由变量\({x\mathop{{}}\nolimits_{{2}}=0,x\mathop{{}}\nolimits_{{4}}=1}\)，得到特解\({x={ \left[ {{\left. \begin{array}{*{20}{l}} {\text{ }2}\\ {\text{ }0}\\ {-2}\\ {\text{ }1} \end{array} \right] }}\right. }}\)

所谓特解，就是特定的解。特定在于给自由变量分配特定的值

这两个向量的任何倍数（\(cx\)）都在零空间内，而零空间就是特解的线性组合，即\({c{ \left[ {{\left. \begin{array}{*{20}{l}} {-2}\\ {\text{ }1}\\ {\text{ }0}\\ {\text{ }0} \end{array} \right] }}\right. }+d{ \left[ {{\left. \begin{array}{*{20}{l}} {\text{ }2}\\ {\text{ }0}\\ {-2}\\ {\text{ }1} \end{array} \right] }}\right. }\text{ }}\)

行最简阶梯矩阵

转换成行最简阶梯矩阵\(R\)，就是在矩阵\(U\)的基础上再把主元化简为1且主元列除主元外全都是0

对于上例：

零空间的另一种解法

把矩阵\(R\)进行“行交换”：

\({R={ \left[ {{\left. \begin{array}{*{20}{l}} {1\text{ }\text{ }0\text{ }\text{ }2\text{ }-2}\\ {0\text{ }\text{ }1\text{ }\text{ }0\text{ }\text{ }2}\\ {0\text{ }\text{ }0\text{ }\text{ }0\text{ }\text{ }0} \end{array} \right] }}\right. }}\)，即\({R={ \left[ {{\left. \begin{array}{*{20}{l}} {I\text{ }\text{ }F}\\ {0\text{ }\text{ }0} \end{array} \right] }}\right. }}\)这种形式。由于最下面是零向量（换成线性方程是\(0=0\)始终成立），可以省略就变成了\({R={ \left[ {{\left. {I\text{ }\text{ }F} \right] }}\right. }}\)

其中\(I\)是一个\(r \times r\)的单位矩阵，\(F\)是自由列消元后的部分

把刚才得出的两个特解组合在一起，即\({ \left[ {{\left. \begin{array}{*{20}{l}} {-2\text{ }\text{ }2}\\ {\text{ }0\text{ }-2}\\ {\text{ }1\text{ }\text{ }\text{ }0}\\ {\text{ }0\text{ }\text{ }\text{ }1} \end{array} \right] }}\right. }\)（经过了“行变换”，即第二行与第三行交换）

观察前两行与\(F\)的差别，得出结论前两行就是\(-F\)，上面的组合可表示为

\[{ \left[ {{\left. \begin{array}{*{20}{l}} {-F}\\ {I} \end{array} \right] }}\right. } \]

从一开始求\(Ax=0\)变成求\(Ux=0\)再变成现在的的\(Rx=0\)，即

\[{{ \left[ {{\left. {I\text{ }\text{ }F} \right] }}\right. }{ \left[ {{\left. \begin{array}{*{20}{l}} {x\mathop{{}}\nolimits_{{pivot}}}\\ {x\mathop{{}}\nolimits_{{free}}} \end{array} \right] }}\right. }=0} \]

现在用一个巧妙的方法解出答案：

构造一个零向量矩阵：\({N={ \left[ {{\left. \begin{array}{*{20}{l}} {}\\ {I} \end{array} \right] }}\right. }}\)形式，\(I\)是\((n-r) \times (n-r)\)（\(n-r\)代表自由列列数）大小的单位矩阵

零空间矩阵满足\(RN=0\)，再由矩阵分块乘法可知:

\[{N={ \left[ {{\left. \begin{array}{*{20}{l}} {-F}\\ {I} \end{array} \right] }}\right. }} \]

与上个方法得到的答案一样

总结对于矩阵\(R\)来说，这个方法就很简单，消元得到\(F\)，再加上\(I\)就行了