第六节 列空间和零空间

第六节 列空间和零空间

子空间的交集和并集

假设有子空间\({D\mathop{{}}\nolimits_{{1}}}\)和\({D\mathop{{}}\nolimits_{{2}}}\)，\({D\mathop{{}}\nolimits_{{1}}}\)是\({R\mathop{{}}\nolimits_{{3}}}\)中过原点的一条直线，\({D\mathop{{}}\nolimits_{{2}}}\)是\({R\mathop{{}}\nolimits_{{3}}}\)中过原点的平面

1. \({D\mathop{{}}\nolimits_{{1}} \not\subset D\mathop{{}}\nolimits_{{2}}}\)

   1. \({D\mathop{{}}\nolimits_{{1}} \cap D\mathop{{}}\nolimits_{{2}}}\)只有一个原点，显然是子空间
   2. \({D\mathop{{}}\nolimits_{{1}} \cup D\mathop{{}}\nolimits_{{2}}}\)则不能构成子空间，因为随便取\({D\mathop{{}}\nolimits_{{1}}}\)中的向量\(a\)和\({D\mathop{{}}\nolimits_{{2}}}\)中的向量\(b\)（\({a \neq b}\)）相加（线性运算）肯定不属于构成的空间，故相并不能构成子空间

2. \({D\mathop{{}}\nolimits_{{1}} \subset D\mathop{{}}\nolimits_{{2}}}\)

   不管交集还是并集都能构成子空间

列空间

1. 列空间即矩阵列和列向量的线性组合构成的向量空间

2. 在第一节中提到一个问题，对于任意的\(b\)，是否都能求出\(Ax=b\)？接下来用向量空间来分析一下

   比如\({A={ \left[ {{\left. \begin{array}{*{20}{l}} {1\text{ }\text{ }1\text{ }\text{ }3}\\ {2\text{ }\text{ }1\text{ }\text{ }3}\\ {3\text{ }\text{ }1\text{ }\text{ }4}\\ {4\text{ }\text{ }1\text{ }\text{ }5} \end{array} \right] }}\right. }}\)，对于这个矩阵就能说明问题答案是否定的

   因为它是由四个线性方程组成，而未知数却只有三个。即它时一个\({R\mathop{{}}\nolimits^{{4}}}\)，却只是充满了\({R\mathop{{}}\nolimits^{{3}}}\)，\(b\)不能表示为矩阵\(A\)的线性组合时，是无解的，只有\(b\)在矩阵\(A\)的列空间里时（\(b\)能表示为矩阵\(A\)的线性组合），才有解

   总结：对于\(Ax=b\)，只有\(b\)是矩阵\(A\)各列向量的线性组合时才有解

   线性相关与线性无关

   \({A={ \left[ {{\left. \begin{array}{*{20}{l}} {1\text{ }\text{ }1\text{ }\text{ }3}\\ {2\text{ }\text{ }1\text{ }\text{ }3}\\ {3\text{ }\text{ }1\text{ }\text{ }4}\\ {4\text{ }\text{ }1\text{ }\text{ }5} \end{array} \right] }}\right. }}\)和\({B={ \left[ {{\left. \begin{array}{*{20}{l}} {1\text{ }\text{ }1\text{ }\text{ }2}\\ {2\text{ }\text{ }1\text{ }\text{ }3}\\ {3\text{ }\text{ }1\text{ }\text{ }4}\\ {4\text{ }\text{ }1\text{ }\text{ }5} \end{array} \right] }}\right. }}\)

   刚才已经忽略一个问题，当矩阵\(A\)的右上角的值改成2时，会发生什么

   矩阵\(B\)前两列的和等于第三列，即是线性相关的，这时候矩阵\(B\)的列向量只能构成\({R\mathop{{}}\nolimits^{{2}}}\)，因为第三列是毫无贡献的。

   而矩阵\(A\)的各列之间都是线性无关的，每一列都能决定一个维度

零空间

1. 矩阵\(A\)的零空间（Nullspace）\(N(A)\)是指满足\(Ax=0\)的\(x\)的集合
2. 比如矩阵\({A={ \left[ {{\left. \begin{array}{*{20}{l}} {1\text{ }\text{ }1\text{ }\text{ }2}\\ {2\text{ }\text{ }1\text{ }\text{ }3}\\ {3\text{ }\text{ }1\text{ }\text{ }4}\\ {4\text{ }\text{ }1\text{ }\text{ }5} \end{array} \right] }}\right. }}\)，因为前两列与第三列是线性相关的，即\(1 \times 列1+2 \times 列2-1 \times 列3=0\)，所以

\(N(A)={ \left[ {{\left. \begin{array}{*{20}{l}} {1}\\ {1}\\ {-1} \end{array} \right] }}\right. }\)

3. 如果存在零空间，矩阵一定有线性相关的列，它们会在消元中体现出来

   \(\left[ \begin{matrix} 1&2&2&2\\ 2&4&6&8\\ 3&6&8&10 \end{matrix} \right] -> \left[ \begin{matrix} 1&2&2&2\\ 0&0&2&4\\ 0&0&0&0 \end{matrix} \right]\)

   提示：为下一节做准备

4. 如果方程是这样：

   

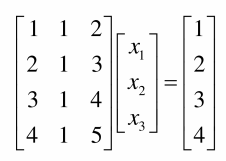
很显然零向量不在解集内，那么这个方程的解集就不能构成一个子空间