第四节 矩阵乘积的逆矩阵

A的LU分解

矩阵乘积的逆矩阵

由\({ABB\mathop{{}}\nolimits^{{-1}}A\mathop{{}}\nolimits^{{-1}}=A \left( BB\mathop{{}}\nolimits^{{-1}} \left) A\mathop{{}}\nolimits^{{-1}}=I\right. \right. }\)

得\({ \left( AB \left) \mathop{{}}\nolimits^{{-1}}=B\mathop{{}}\nolimits^{{-1}}A\mathop{{}}\nolimits^{{-1}}\right. \right. }\)

矩阵乘积的转置

本节先提前提一下转置，下节会详细讲转置

把矩阵\(A\)的转置记为\({A\mathop{{}}\nolimits^{{T}}}\)，对矩阵\(A\)的转置就是把矩阵\(A\)的行变为矩阵\({A\mathop{{}}\nolimits^{{T}}}\)的列，把矩阵\(A\)的列变为矩阵\({A\mathop{{}}\nolimits^{{T}}}\)的行

例：\({A={ \left[ {{\left. \begin{array}{*{20}{l}} {1\text{ }\text{ }2\text{ }\text{ }3}\\ {4\text{ }\text{ }5\text{ }\text{ }6} \end{array} \right] }}\right. },A\mathop{{}}\nolimits^{{T}}={ \left[ {{\left. \begin{array}{*{20}{l}} {1\text{ }\text{ }4}\\ {2\text{ }\text{ }5}\\ {3\text{ }\text{ }6} \end{array} \right] }}\right. }}\)

矩阵乘积的转置：

\({ \left( AB \left) \mathop{{}}\nolimits^{{T}}=B\mathop{{}}\nolimits^{{T}}A\mathop{{}}\nolimits^{{T}}\right. \right. }\)

转置矩阵的逆矩阵

公式：\({ \left( A\mathop{{}}\nolimits^{{T}} \left) \mathop{{}}\nolimits^{{-1}}= \left( A\mathop{{}}\nolimits^{{-1}} \left) \mathop{{}}\nolimits^{{T}}\right. \right. \right. \right. }\)

证明：

\({\begin{array}{*{20}{l}} {AA\mathop{{}}\nolimits^{{-1}}=I \xrightarrow {\text{两}\text{边}\text{转}\text{置}} \left( AA\mathop{{}}\nolimits^{{-1}} \left) \mathop{{}}\nolimits^{{T}}=I\mathop{{}}\nolimits^{{T}}\right. \right. }\\ { \xrightarrow {\text{根}\text{据}\text{矩}\text{阵}\text{乘}\text{积}\text{的}\text{转}\text{置}\text{公}\text{式}} \left( A\mathop{{}}\nolimits^{{-1}} \left) \mathop{{}}\nolimits^{{T}}A\mathop{{}}\nolimits^{{T}}=I\right. \right. }\\ { \xrightarrow {\text{根}\text{据}\text{逆}\text{矩}\text{阵}\text{公}\text{式}} \left( A\mathop{{}}\nolimits^{{-1}} \left) \mathop{{}}\nolimits^{{T}}= \left( A\mathop{{}}\nolimits^{{T}} \left) \mathop{{}}\nolimits^{{-1}}\right. \right. \right. \right. } \end{array}}\)

矩阵的LU分解

通过上节课可以知道矩阵\(A\)通过一系列消元矩阵\(E\)得到矩阵\(U\)

比如一个二阶矩阵，通过一次消元就可以达到效果：

\(\begin{array}{*{20}{l}} {{ \left[ {{\left. \begin{array}{*{20}{l}} {\text{ }1\text{ }\text{ }\text{ }0}\\ {-4\text{ }\text{ }1} \end{array} \right] }}\right. }{ \left[ {{\left. \begin{array}{*{20}{l}} {2\text{ }\text{ }1}\\ {8\text{ }\text{ }7} \end{array} \right] }}\right. }={ \left[ {{\left. \begin{array}{*{20}{l}} {2\text{ }\text{ }1}\\ {0\text{ }\text{ }3} \end{array} \right] }}\right. }}\\ {\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }E\mathop{{}}\nolimits_{{21}}A=U} \end{array}\)

由\({E\mathop{{}}\nolimits_{{-1}}^{{21}}E\mathop{{}}\nolimits_{{21}}A=E\mathop{{}}\nolimits_{{-1}}^{{21}}U \to A=E\mathop{{}}\nolimits_{{-1}}^{{21}}U}\)

由于\({E\mathop{{}}\nolimits_{{-1}}^{{21}}}\)是\({E\mathop{{}}\nolimits_{{21}}}\)的逆操作，\({E\mathop{{}}\nolimits_{{21}}}\)是矩阵\(A\)第二行减去4倍的第一行得到，所以\({E\mathop{{}}\nolimits_{{21}}}\)加上4倍的第一行就得到\({E\mathop{{}}\nolimits_{{-1}}^{{21}}}\)

结果为：

\({\begin{array}{*{20}{l}} {{ \left[ {{\left. \begin{array}{*{20}{l}} {2\text{ }\text{ }1}\\ {8\text{ }\text{ }7} \end{array} \right] }}\right. }={ \left[ {{\left. \begin{array}{*{20}{l}} {1\text{ }\text{ }\text{ }0}\\ {4\text{ }\text{ }1} \end{array} \right] }}\right. }{ \left[ {{\left. \begin{array}{*{20}{l}} {2\text{ }\text{ }1}\\ {0\text{ }\text{ }3} \end{array} \right] }}\right. }}\\ {\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }A=LU} \end{array}}\)

其中\(U\)为上三角矩阵（Upper triangular matrix），\(L\)即下三角矩阵（Lower triangular matrix）

还可以再次分解得到\(D\)（diagonal matrix）：

\({\begin{array}{*{20}{l}} {{ \left[ {{\left. \begin{array}{*{20}{l}} {2\text{ }\text{ }1}\\ {8\text{ }\text{ }7} \end{array} \right] }}\right. }={ \left[ {{\left. \begin{array}{*{20}{l}} {1\text{ }\text{ }\text{ }0}\\ {4\text{ }\text{ }1} \end{array} \right] }}\right. }{ \left[ {{\left. \begin{array}{*{20}{l}} {2\text{ }\text{ }0}\\ {0\text{ }\text{ }3} \end{array} \right] }}\right. }{ \left[ {{\left. \begin{array}{*{20}{l}} {1\text{ }\text{ }1/2}\\ {0\text{ }\text{ }\text{ }\text{ }\text{ }1} \end{array} \right] }}\right. }}\\ {\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }A=\text{ }\text{ }\text{ }\text{ }L\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }D\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }U} \end{array}}\)

对于三阶矩阵消元：

\({E\mathop{{}}\nolimits_{{32}} \left( E\mathop{{}}\nolimits_{{31}} \left( E\mathop{{}}\nolimits_{{21}}A \left) \left) =U\right. \right. \right. \right. }\)

如果有下面这种情况：

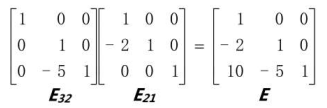
会出现10这种情况，再更大的矩阵可能会有更大的数

利用\(LU\)分解：

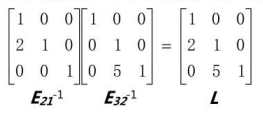
就不会出现上面的那种情况，简化计算

矩阵消元的运算量

在一些矩阵应用中，往往会处理超大的矩阵，即便使用计算机进行处理，也要考虑时间复杂度

对于一个\(n \times n\)的矩阵，假如一次乘法和加法算一次操作，那么需要多少次操作才能完成所有的消元？

一行要进行\(n\)次运算，\(n-1\)行要进行\({n \times \left( n-1 \left) \approx n\mathop{{}}\nolimits^{{2}}\right. \right. }\)次运算，得到第一列的结果，后面以此类推，得到共需要消元次数：\({{n\mathop{{}}\nolimits^{{2}}}+ \left( n-1 \left) \mathop{{}}\nolimits^{{2}}+\text{ ……}+2\mathop{{}}\nolimits^{{2}}+1\mathop{{}}\nolimits^{{2}}={\mathop{ \sum }\limits_{{i=1}}^{{n}}{i\mathop{{}}\nolimits^{{2}} \approx {\mathop{ \int }\nolimits_{{0}}^{{n}}{x\mathop{{}}\nolimits^{{2}}dx}}=\frac{{1}}{{3}}n\mathop{{}}\nolimits^{{3}}}}\right. \right. }\)

这是求变换\(A\)需要多少次操作，那么对于右侧常数列\(b\)，易得其需要\(n\mathop{{}}\nolimits^{{2}}\)级别操作，而我们经常会遇到矩阵\(A\)和好几个右侧向量\(b\)的情形，所以如果我们之前花时间将\(A\)先分解为\(LU\)，那么之后就可以以较少操作次数去处理每一个右侧向量\(b\)了