1.本周学习总结#
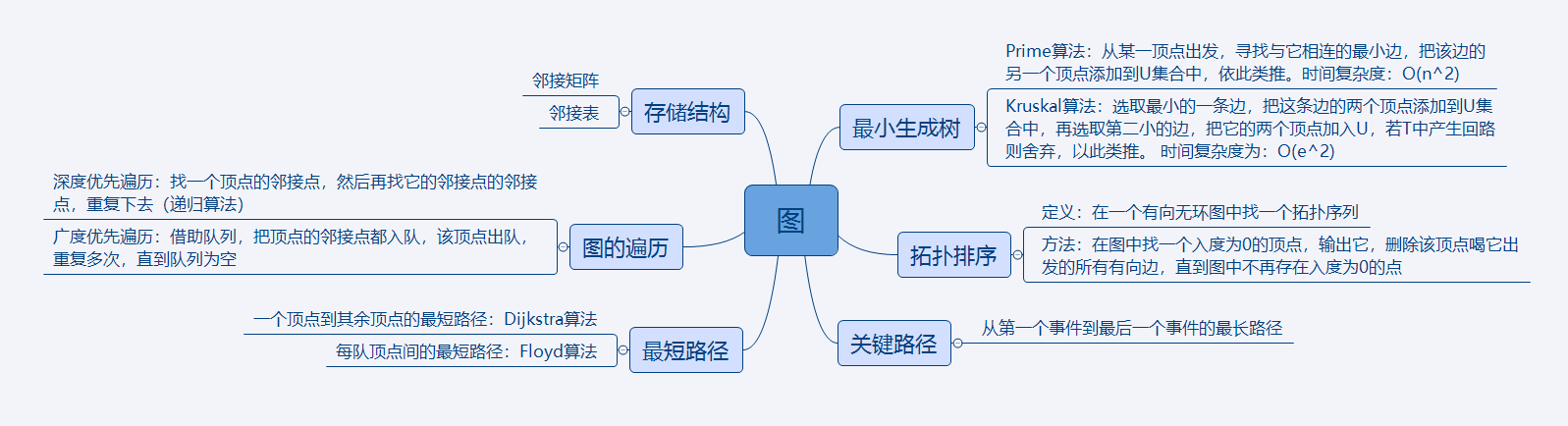
1.思维导图##
2.谈谈你对图结构的认识及学习体会。##
通过对图的学习,认识到了图的两种储存方法,还有图的深度遍历和广度遍历。相对树来说,本章学习的算法较多,如解决最小生成树问题的Prime、Kruskal算法,最短路径的Dijkstra、Floy算法。课后要及时巩固复习,不然真的很容易混淆起来。不仅要知道它们的原理,还要掌握算法的代码。其中,我个人觉得,Prime算法会比Kruskal算法复杂一点,Prime算法随着加入一个顶点,该顶点的最小边可能就需要修改。而Kruskal算法只要依此找最小边,确保它们不会出现回路。
图与树并不是毫不相关的两种结构,在上述算法中,图就转化成树来解决问题。树和图还是挺相似的,都是结点与结点间相互联系,但图的结构更复杂一些。图的结构适合去解决像公路村村通的问题,道路就像一张网,每条路都是相连在一起的。利用图的结构去解决这类问题再合适不过了。
2.PTA实验作业#
2.1题目1: 图着色问题##
2.1.1设计思路(伪代码)###
int main
定义color数组存放每个顶点的颜色
定义count数组
AdjGraph *G;
定义n,e,p,num,k
输入n,e,p
调用CreateAdj函数
输入颜色个数num
for j=0 to num
k=0;
color数组初始化为0
for i=1 to G->n
{
cin>>color[i];
count[color[i]]++;
}
统计count数组中值不为0的个数
if(k!=p)
cout<<"No"<<endl;
else
{
if(Judge(G,color)==1)
cout<<"Yes"<<endl;
else
cout<<"No"<<endl;
}
void CreateAdj
创建一个结点p,存放邻接点,采用头插法插入结点p
int Judge
遍历每个顶点
判断它的邻接点中是否有和它颜色相同的
如果有就return 0
没有就return 1
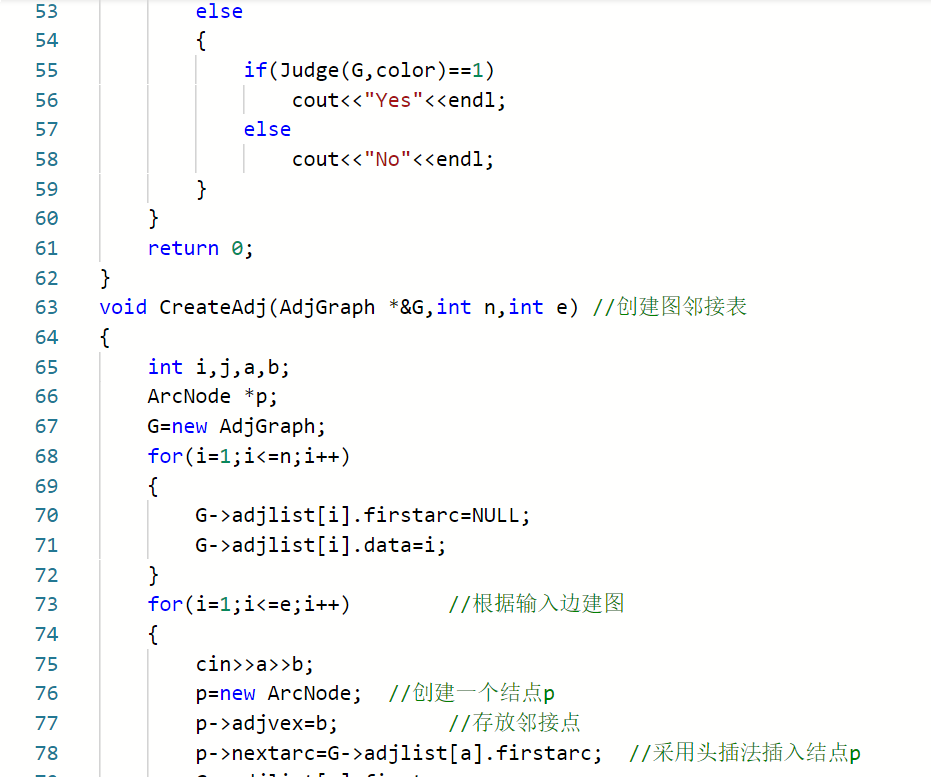
2.1.2代码截图###



2.1.3本题PTA提交列表说明。###
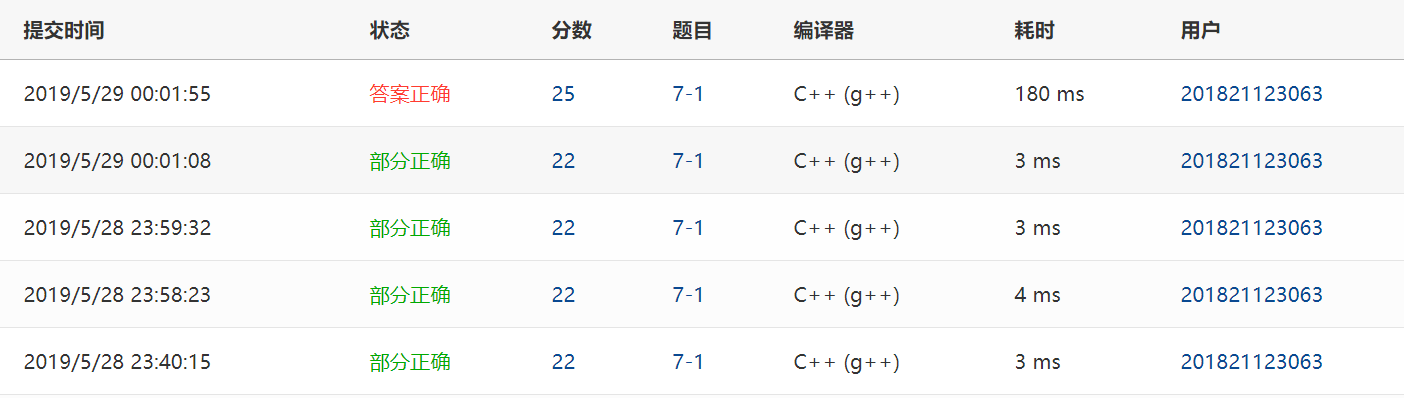
Q1:计算颜色种数的时候出错了,最大图的测试点出现段错误
A1:输入多组颜色数据后,count数组要初始化为0,一开始的代码为color[502]={0},但发现并没有将color数组初始化,就用循环将数组的每个元素置为0。段错误是因为没有注意到题目的要求,color数组和count数组长度定义的太小了。
2.2题目2:六度空间##
2.2.1设计思路(伪代码)###
定义全局变量
int n,m;
int count;
int a[10001][10001]={0};
int main
{
定义 i,b,c;
输入n,m
for i=0 to m
输入b,c
a[b][c]=1;
a[c][b]=1;
for i=1 to n
count=1;
调用函数BFS(i);
输出结点数占结点总数的百分比
}
void BFS(int x)
定义数组visited
定义队列q
定义i,j
定义level = 0 记录层数
定义last = x 记录当前层数的最后一个元素
定义tail 指向下一层最后一个元素
把x入队
visited[x]=1
while(!q.empty())
{
取队头元素x
x出队
for i=1 to n
{
if visited[i]==0&&a[x][i]==1
count++;
tail=i;
visited[i]=1;
i进队
}
if last==x
level自增
修改last的值为tail
如果level等于6结束循环
}
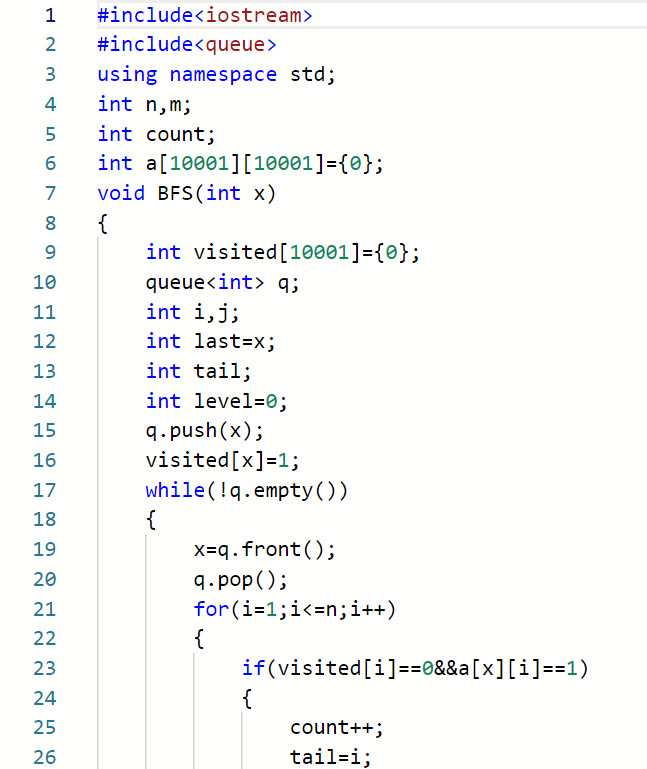
2.2.2代码截图###

2.2.3本题PTA提交列表说明。###
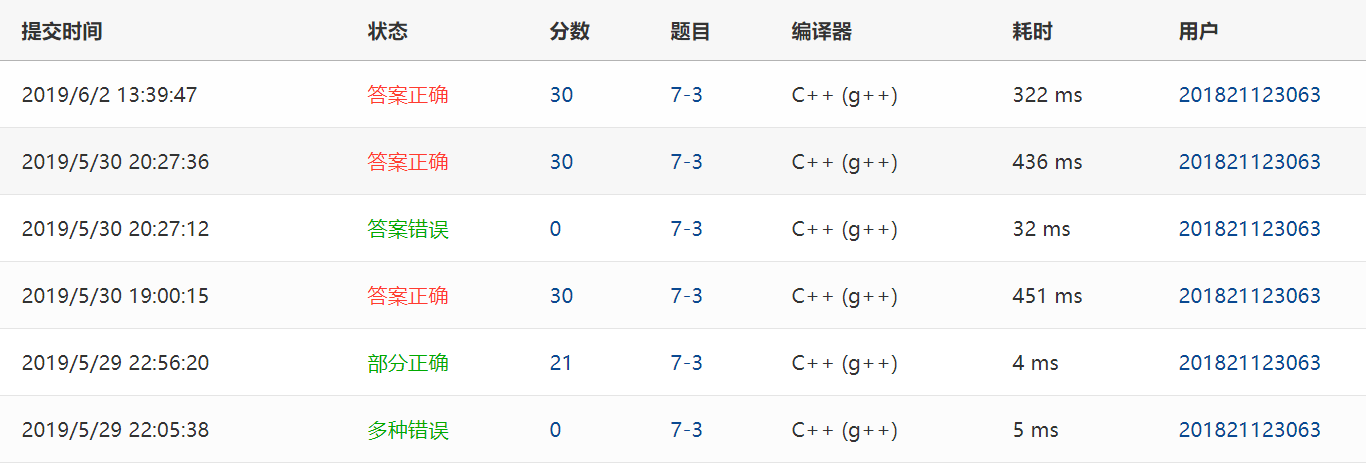
原本是用邻接表做,提交后只有21分,一直有问题。就网上找了这个代码,比原来的简洁。把顶点的邻接点进队,用last,tail,level分别记录当前层数的最后一个元素、下一层最后一个元素、层数,用这三个元素作为寻找与每个顶点每相距不超过6的结点,统计这些结点个数。只有当last等于队头元素时,level才自增,last才修改为tail,当level的值达到6,提前退出循环。
2.3题目3:公路村村通##
2.3.1设计思路(伪代码)###
定义全局变量
int s=0,n,e;
int g[4000][4000];
int lowcost[4000],closest[4000];
int main
{
输入n,e
调用函数CreateMGraph(n,e)
if(Prim(1)==1)
输出s
else
输出-1
}
void CreateMGraph(int n,int e )
定义i,j,a,b,c
数组所有元素初始化为9999
for i=1 to e
输入a,b,c
g[a][b]=c;
g[b][a]=c;
g[i][i]=0;
int Prim(int v)
定义min,i,j,k;
for i=1 to n
{
lowcost[i]=g[v][i];
closest[i]=v;
}
for i=1 to n
{
min=9999;
for j=1 to n
{
如果 lowcost[j]的值不为0且小于min
min=lowcost[j];
k=j;
}
if min==9999
返回0
s+=min;
标记k已经加入U lowcost[k]置为0
for j=1 to n
如果g[k][j]的值不为0且小于lowcost[j]就对顶点进行调整
lowcost[j]=g[k][j];
closest[j]=k;
}
返回1
2.3.2代码截图###


2.3.3本题PTA提交列表说明。###
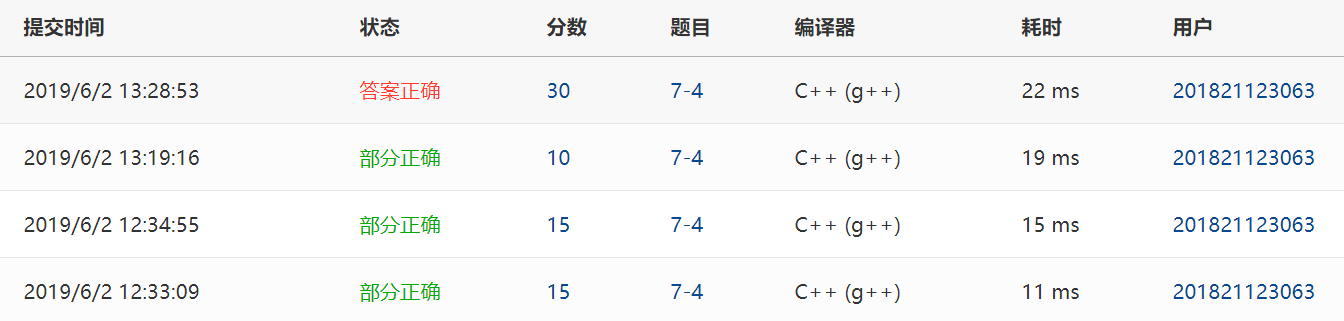
Q1:部分正确
A1:数组g没有设初值,导致在判断输入数据不足以保证畅通的情况出现错误。该题采用Prime算法,参考了书上的代码。但一开始没有理解书上min=INF的意思,后来参考了同学代码,将min设为不存在边的g数组的值。通过循环,来判断各个顶点与其他顶点是否存在边,既min的值有没有被改变,从而输出-1。
3、上机考试错题及处理办法#
3.1截图错题代码##



3.2 错的原因及处理方法##
这题按自己的做法只能部分正确,于是网上找了代码,网上的代码更简洁,但没有真正理解代码,把if(last==x)、if(level==6)的这两段代码放到for循环中,发现输出结果错误后,又把那两段代码放到if(visited[i]==0&&a[w][i]==1)里面,结果还是错误的。应该是先把所有顶点都入队后,再开始后面的操作。所以if(last==x)、if(level==6)的这两段代码要放在for循环外面,问题就解决了。



