1.本周学习总结#
1.思维导图##
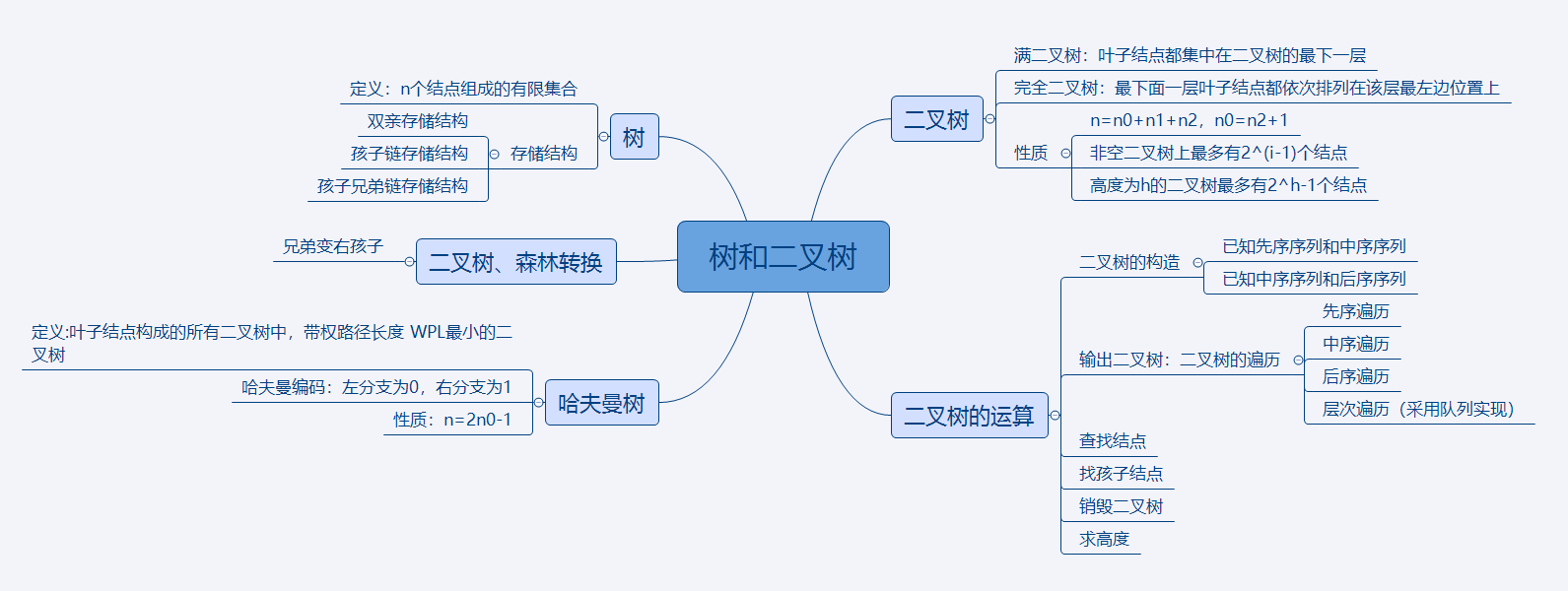
2.谈谈你对树结构的认识及学习体会。##
相比前面的内容,树的学习难度加大了。树包括孩子结点、兄弟结点、双亲结点,树的遍历顺序有先序遍历、中序遍历、后序遍历、层次遍历。可以根据先序遍历和中序遍历或中序遍历和后序遍历来还原树,转换成代码就需要找一下其中的规律。
树中哈夫曼树的带权路径长度达到最小,也叫最优二叉树。哈夫曼树的建立要把权值较小的结点放较下层,权值较大的结点要越靠近根结点。
树的应用与递归密切相关,所以我们要捋清递归的规则,知道它的执行原理,才能应用递归来解决问题。一级级调用,再一级级返回。
2.PTA实验作业#
2.1.题目1:6-4 jmu-ds-表达式树##
2.1.1设计思路(伪代码)###
void InitExpTree(BTree &T,string str) //建表达式的二叉树
定义栈s存放数字
定义栈op存放运算符
先将‘#’进op栈
while(str[i])
{
if str[i]是数字
T=new BiTNode;
T->data=str[i++];
T的左右孩子置为NULL
T进栈s
else
调用Precede函数比较op栈顶元素与str[i]大小
如果函数值为'<'
str[i]进op栈
如果函数值为'='
op栈出栈
如果函数值为'>'
str[i]进op栈
T=new BiTNode;
op栈顶元素赋值给T->data
T->rchild=s.top();
s栈出栈
T->lchild=s.top();
s栈出栈
s.push(T);
op栈出栈
}
while(op栈顶元素不是'#') //把树结点的关系连起来
{
T=new BiTNode;
op栈顶元素赋值给T->data
op栈出栈
T->rchild=s.top();
s栈出栈
T->lchild=s.top();
s栈出栈
s.push(T);
}
double EvaluateExTree(BTree T)计算表达式树
定义a,b
if 树T不空
if 左右孩子都为空
return T->data-'0';
a=EvaluateExTree(T->lchild)
b=EvaluateExTree(T->rchild)
判断T->data
如果是'+'
return a+b
如果是'-'
rerurn a-b
如果是'*'
return a*b
如果是'/'
if b==0
输出divide 0 error!
退出程序
否则
return a/b
2.1.2代码截图(注意,截图,截图,截图。不要粘贴博客上。)###
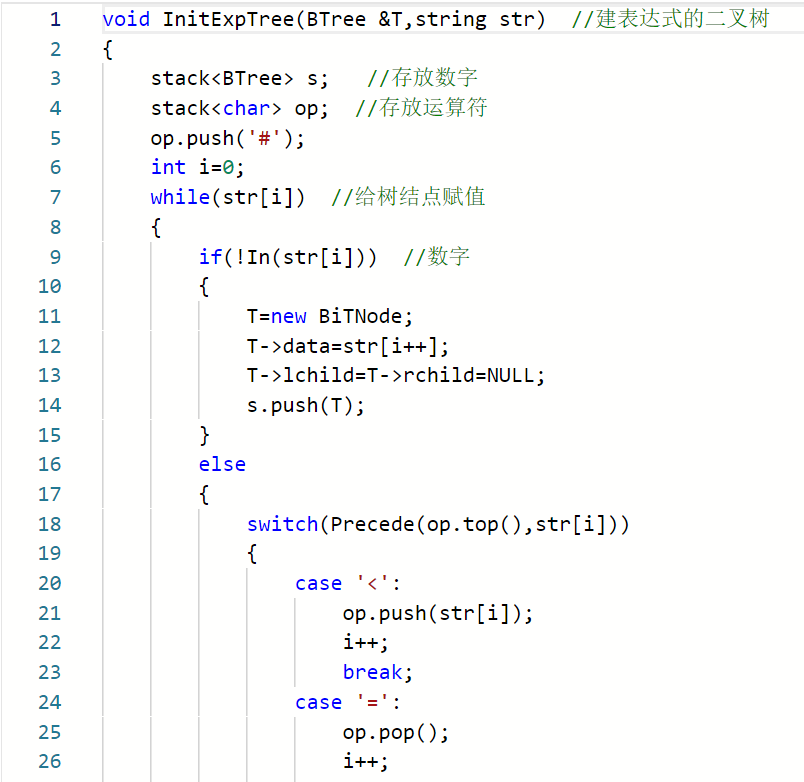

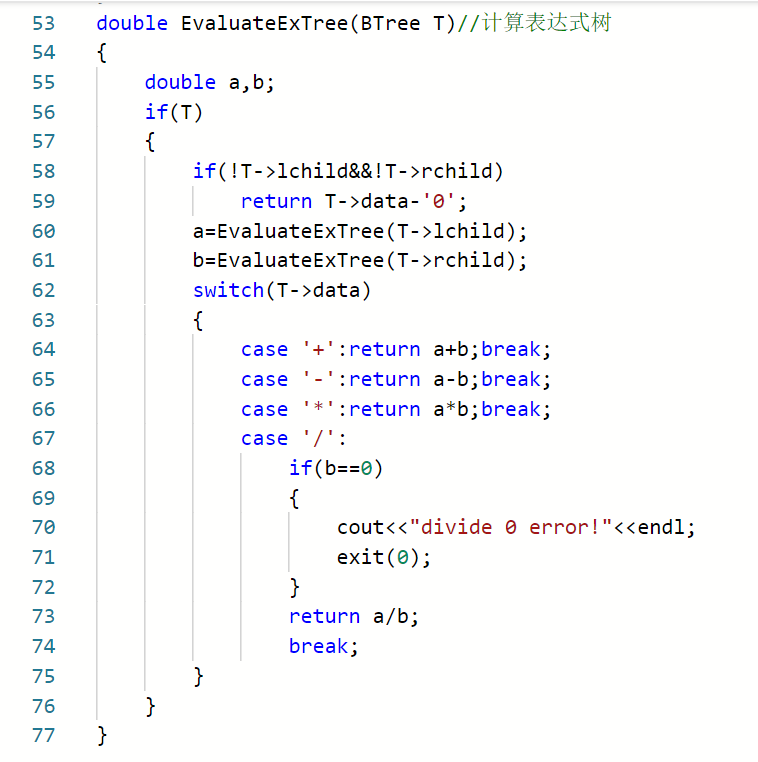
2.1.3本题PTA提交列表说明。###

Q1:把表达式建成树比较有难度
A1:叶子结点都是表达式中的数字,首先遇到数字就赋值给树结点,然后把结点进s栈。遇到运算符就比较复杂了,先要判断运算符和op栈顶元素的大小。若该运算符大于op栈顶元素,就要先把op栈顶元素和s栈里元素关系先建起了。小于则把运算符进op栈。等于则栈顶元素出栈。最后再把栈s、op的关系建起来,op里面的元素为根结点,s栈里面的元素为根的左右孩子。再把新建成的分支进s栈,重复操作,直到op栈顶元素不是'#'。
2.2 题目2:7-4 jmu-ds-二叉树叶子结点带权路径长度和##
2.2.1设计思路(伪代码)###
定义树的结构体
主函数做建树函数的调用和计算带权路径长度和
BinTree CreateBtree(string str,int i)
定义BinTree树BT
if i>str.size()-1
return NULL;
if str[i]=='#'
return NULL;
生成新结点BT
BT->Data=str[i];
BT->Left=CreateBtree(str,2*i);
BT->Right=CreateBtree(str,2*i+1);
return BT;
void GetWpl(BinTree BT,int &wpl,int h)
if BT==NULL
return ;
else
if BT的左右孩子都为空
wpl+=h*(BT->Data-48); //字符转数字(减去'0'=48)
h开始重新记录置为0
h++;
GetWpl(BT->Left,wpl,h);
GetWpl(BT->Right,wpl,h);
2.2.2代码截图(注意,截图,截图,截图。不要粘贴博客上。)###
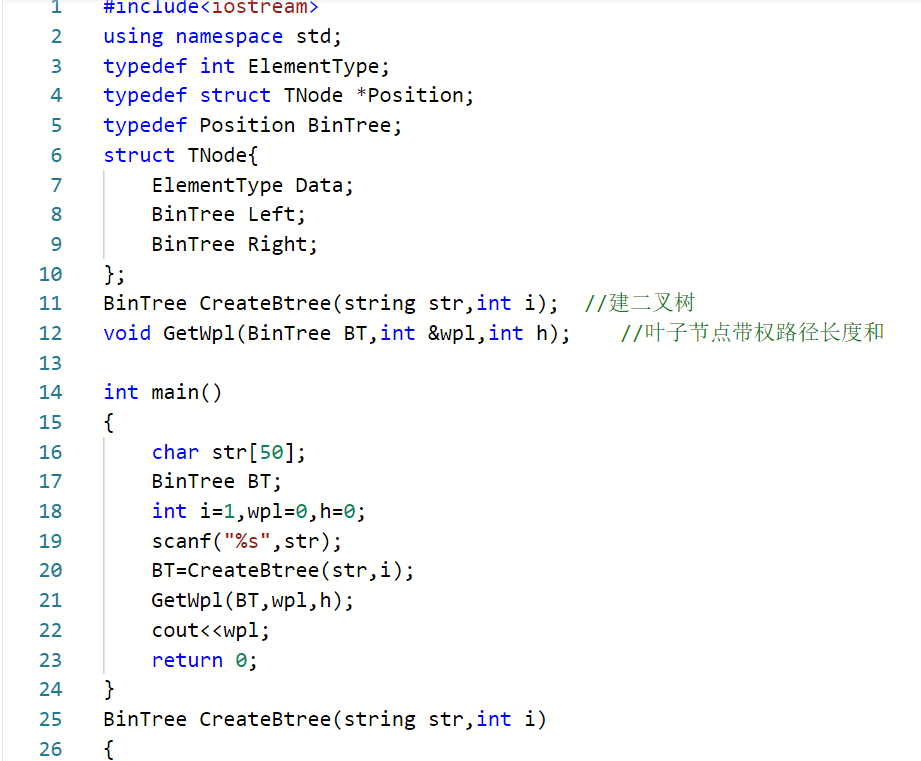
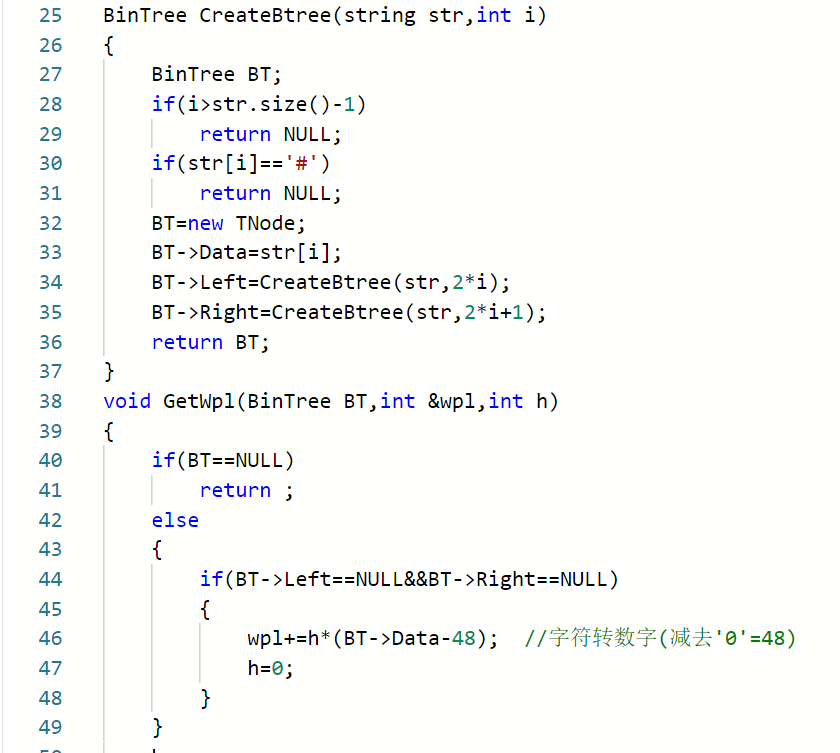
2.2.3本题PTA提交列表说明。###

Q1:刚开始在编译器上运行的结果不是题目中的72
A1:计算wpl时,直接这么写wpl+=h*BT->Data,忘记BT->Data是字符,不是数字,所以计算出来的当然不是72。应该改成wpl+=h*(BT->Data-48),要再减去字符'0'即可,还有就是计算wpl后,h要置为0,用于其他叶子结点计算wpl。
2.3 题目3:7-5 jmu-ds-输出二叉树每层节点##
2.3.1设计思路(伪代码)###
先按题目递归法建树
void LevelOrder(BinTree BT) //层次遍历
定义BinTree型队列qt;
定义int型level,flag;
定义BinTree型curNode,lastNode;
curNode=lastNode=BT;
if BT==NULL
输出NULL
return ;
else
BT进队
while(!qt.empty())
{
if curNode==lastNode
{
level++;
用flag来控制输出level:前是否要换行
lastNode=qt.back();
}
curNode=qt.front();
输出curNode->Data
if curNode->Left非空
curNode->Left进队
if curNode->Right非空
curNode->Right进队
出队
}
2.3.2代码截图(注意,截图,截图,截图。不要粘贴博客上。)###
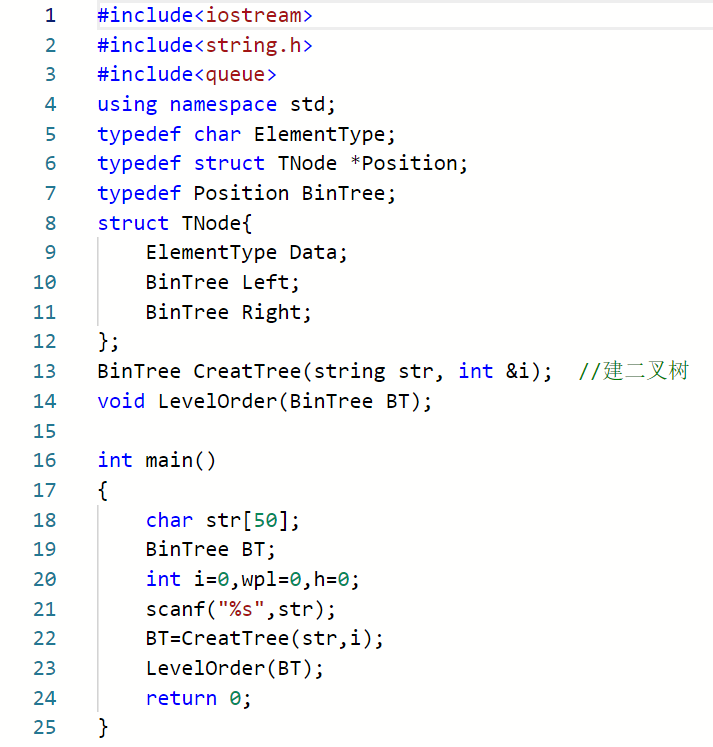
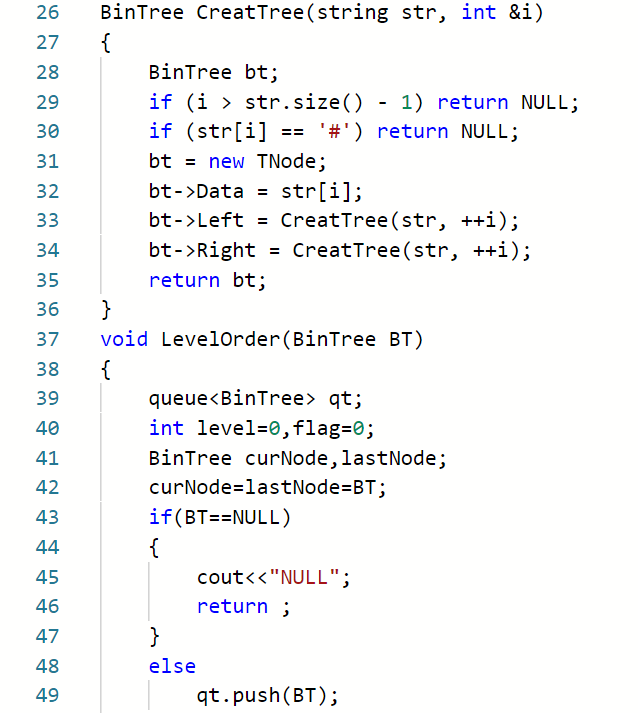

2.3.3本题PTA提交列表说明。###

Q1:怎么知道每层结点有哪几个
A1:将根结点进栈,先将curNode,lastNode都置为BT。只有当curNode,lastNode相等时,即curNode到达每层最后一个元素,再输出层次。用curNode记录队头,把队头的左右孩子进队,用lastNode记录队尾。重复操作,直到队列为空。
3、阅读代码#
3.1 题目##
二叉树剪枝
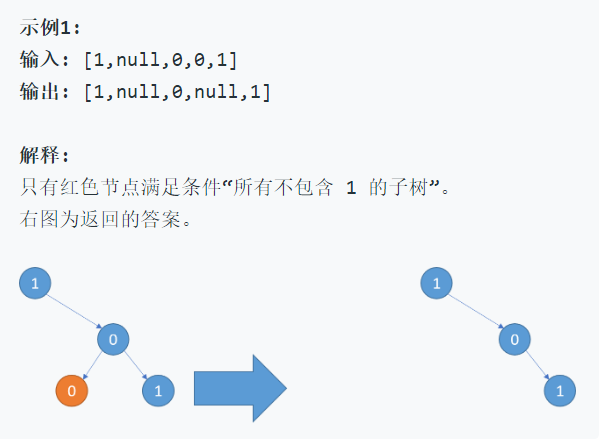
给定二叉树根结点 root ,此外树的每个结点的值要么是 0,要么是 1。返回移除了所有不包含 1 的子树的原二叉树。
3.2 解题思路##
该题采用后序遍历的方法,若树为空,则返回null。接着递归左子树和右子树。若有结点左、右孩子都为空,且该结点的值为0,则返回努力了,否则返回root
3.3 代码截图##
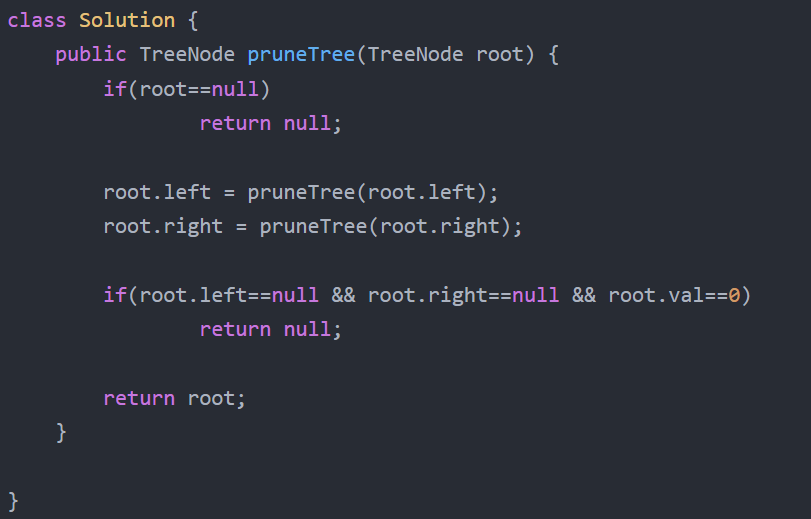
3.4 学习体会##
这题虽然做法是递归,但先序遍历和后序遍历有差别,采用先序遍历则行不通。因为前序只能删除叶子结点为0的,但非叶子为0并且左右结点为0的情况却不行。而采用后序遍历,效果就不同了,后序遍历从叶子结点开始判断删除,若有上述情况,则那个结点也能成为叶子结点,从而被删掉。
所以我们要全面看待问题,不同顺序遍历效果可能是不同的,这种遍历顺序行不通,其他种遍历顺序也许就别有洞天,这道题就是一个很好的案例。



