阅读笔记: Map-Based Precision Vehicle Localization in Urban Environments
摘要
结合了GPS、IMU、轮速计和LiDAR数据,生成高精度的环境地图。使用了与近期的SLAM方法类似的offline relaxation技术,把地图在相交区域和自我重叠区域进行对齐。通过把最终的地图简化到平地表面,可以把其它车辆形成的印记移除。最终的得到的是2D的5cm像素分辨率地面红外反射率图像。
定位时使用粒子滤波把LiDAR测量关联到这样的地图上,实现了10厘米的实时定位。
(这篇论文大部分篇幅是介绍怎么构建因子图来建图)。
使用GRAPHSLAM进行道路建图
A 运动建模
Pose之间通过车辆的惯导系统获取的Odometry数据连在一起,记\(x_t\)为t时刻的位姿:
其中g为非线性动力学函数,\(\epsilon_t\)为为零均值高斯噪声,协方差为\(R_t\)。在log似然的形式中,每一步运动都引入一个二次约束:
如论文【10,30】中一样,这些约束可以看成是一个稀疏Markov graph的边。
B 地图表达
地图是一个2D的网格,可以对环境中每个x-y位置都给出一个红外反射率值。因此,我们可以把地面地图当作一个拼起来的地面的红外激光反射图像。
为了获得这样的地图,多个LiDAR装在车上朝下指向路面。
为了消除动态物体对之后的定位的影响,我们对每个LiDAR拟合一个地平面,只保留与这个地平面重合的观测。这样就只有平的地面被建图。
对于任何pose \(x_t\)和任何(固定且已知)相对于自车坐标系的角度\(\alpha_i\),期望的反射率可以很容易得到。令\(h(m, x_t)\)为这样一个函数,对于给定的地图m,位姿\(x_t\)和激光角度\(\alpha_i\),它可以计算出期望的反射率。我们将观测过程建模为:
其中$ \delta_t^i = N(0, Q_t)$。
在log似然的形式中,这提供了一个新的约束集:
这个函数中的未知量是位姿x_t和地图m。
C 对GPS的隐变量拓展
记y_t为t时刻的GPS信号。咋一看,我们可能整合GPS通过目标函数中J中的一个额外约束。得到的约束形如:
其中\(\Gamma\)为GPS信号的协方差。然而,这种形式假设GPS噪声是独立的。实际上,GPS信号受制于系统噪声,因为GPS被大气层特性影响,它会随着时间慢慢改变。
我们的方法将系统内在噪声建模为Markov chain模型,使用GPS bias项\(b_t\)作为隐变量。这个假设是说GPS实际上被一个不可观的加性bias b_t影响(因此它的latent但是可以通过数据推断出来)。这个模型得到的约束如下:
在此模型中,隐变量bias b_t受制于随机游走:
其中\(\beta_t = N(0, S_t)\)。常量\(\gamma < 1\)慢慢地将bias b_t拉到0。
D 扩展后的GraphSLAM目标函数
把上面那些放到一起,可以得到:
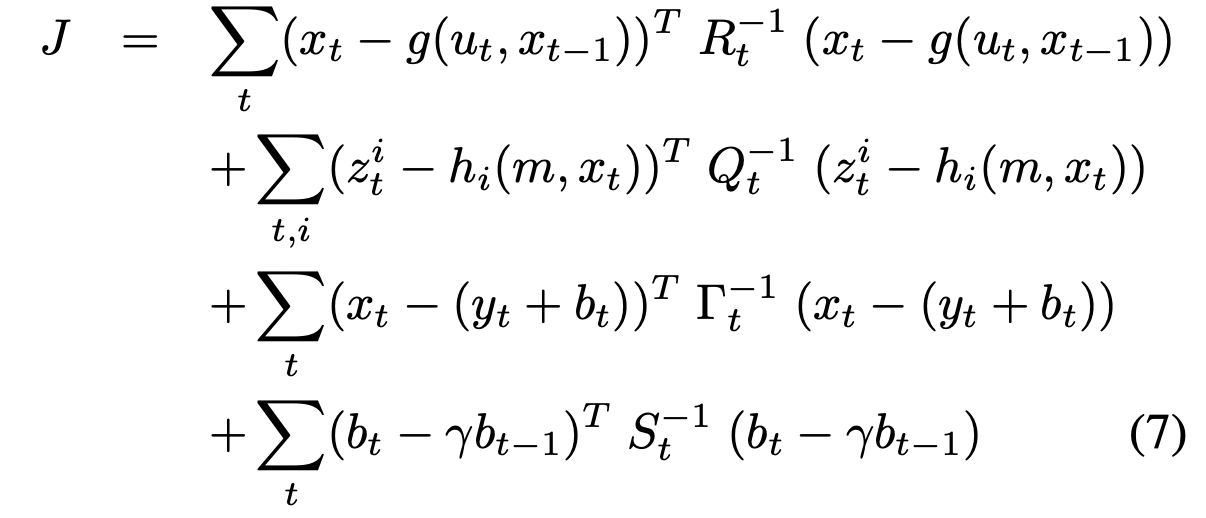
然而,unfortunately,这个表达式没法直接优化,因为它涉及到多达百万个变量(poses和map pixels)。
E 将地图Integrating out(积分掉?)
Unfortunately,直接优化J在计算上是不现实的。我们采用了GraphSLAM中的关键一步——首先把地图变量积分出去。具体而言,我们不是对所有的变量{x_t}、{b_t}和m优化J,我们先优化一个仅包含位姿x_t和bias b_t的J的简化版本,之后再计算最可能的地图。这是由文献[30]中所说的一个事实所启发——地图变量可以在SLAM联合后验中积分出去。因为几乎系统中几乎所有的未知变量都是地图,这一简化使得优化J的问题简单了很多,从而可以高效求解。
对于某个surface patch在建图过程中只被看到一次的情况,我们的方法可以在位姿对齐过程中简单地忽略相关的地图变量,因为这样的patches对位姿估计没有影响。因此,我们可以放心地把相关约束从目标函数J中移除,不用担心对poses的目标函数。
然而,那些被不止一次观测到的位置是需要关注的。在这些位置,它们确实构建了位姿间的约束。这些约束就是SLAM中著名的loop closure问题。为了把这些地图变量积分出去,我们采用一种叫做map matching的方法来进行高效近似。Map matching通过比较局部子图来找到最佳的对齐位姿。
我们执行map matching时,首先寻找重叠区域,然后构建局部子图。重叠区域是由于在同样的地方经过两次得到的。正式地说就是,这种重叠区域被定义为两个不相邻的时间索引序列,{t_1, t_2, ...} 和{s_1, s_2, ...},如果地图中相关的网格数量超过一定阈值就认为是重叠的。
一旦这样的重叠区域被找到,我们就构建两个独立的地图。其中一个只使用{t_1, t_2, ...}的数据,而另一个只使用{s_1, s_2, ...}的数据。然后假设两者在重叠区域都符合单一最大似然的反射率地图,搜索最大化观测概率的alignment。
具体而言,通过计算这些子图之间的线性correlation field,得到它们之间的x-y offset。由于位姿在alignment之前都已经用GPS和IMU数据后处理过,我们发现匹配之间的旋转误差是微不足道的。因为其中一个或者两个子图可能是不完整的,我们只用那些反射率值已知的像素进行相关性系数计算。如果alignment是唯一的,我们直接找到这个correlation field中的单个peak。这个peak就认为是local alignment的最佳估计。相对的偏移量记为\(\delta_{st}\),上述得到的约束被加入到目标函数J中。
这个地图匹配步骤引入下列约束到目标函数J中:
其中\(\delta_{st}\)为位姿x_t和位姿x_s之间的局部偏移,L_st为这个约束的强度(协方差的逆)。用这个新约束替代地图变量明显是一种近似,不过,这样才使得优化问题可解。
这样新的目标函数中很多与观测模型有关的项就被数量更少的位姿间约束所替代。得到的形式如下:
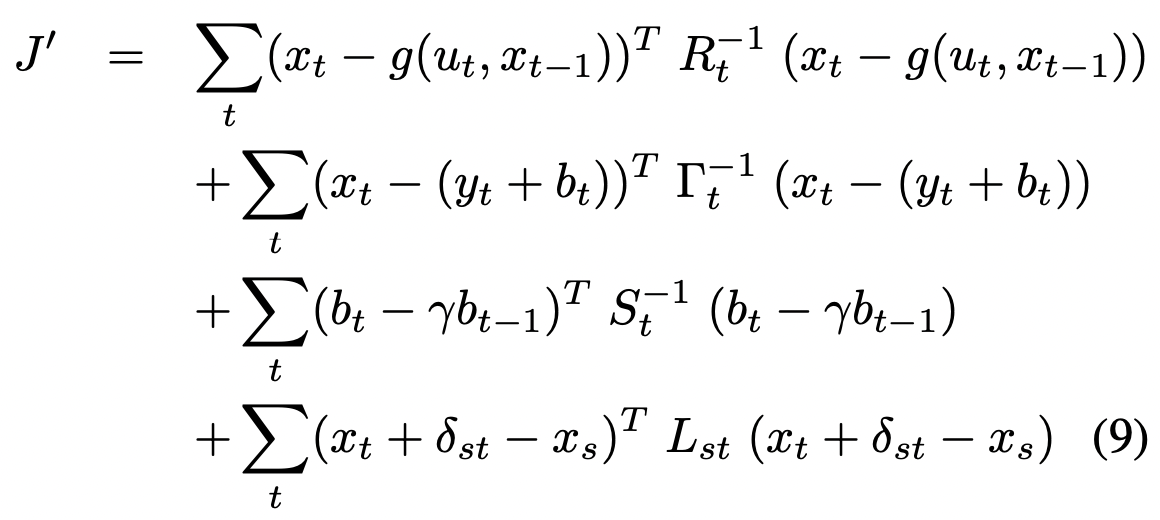
这个目标函数不包含地图变量,因此变量数量低了几个数量级,就可以很容易地通过CG求解。对于本文中展示的地图类型,在一台PC上优化所花的时间明显比加载数据的时间少。大部分时间花在局部地图之间的连接,J'的优化只花了几秒。得到的是一个调整后的解决intersection的不一致性的轨迹
地图的计算
为了得到地图,我们需要对所有存在一个或多个观测的位置填上地图值。对于有多个观测的网格,我们计算平均反射率来最小化联合(观测)数据似然函数。我们注意到这等效于优化J中缺失的约束,记为J'':
假设位姿x_t是已知的。再一次地,对于本文采用的地图类型,对齐的位姿的计算只需要几秒。在渲染一个用于定位和显示的地图时,我们的实现利用硬件加速的OpenGL来渲染平滑的插值后的多边形,这些多边形的节点基于随着机器人穿过它的轨迹返回的三个激光雷达的距离和的反射强度。
实时定位
A 使用粒子滤波定位
Localization使用上述得到的地图,为了确定车辆相对于地图的位置。Localization实时运行,以200Hz的运动更新。
我们的方向使用与之前的章节一样的数学变量建模。不过,为了实现实时性能,我们使用粒子滤波维护一个三维位姿向量x, y , yaw。其它量假设足够精确。粒子滤波中的运动预测基于惯性速度测量。
观测通过惯常的方式进行整合——通过影响重要性权重并设置重采样概率。只有那些对应的地图存在定义的观测会被整合,也就是说地图中有一个先验的反射率值。对于观测更新,第k个粒子的权重由下式给出:
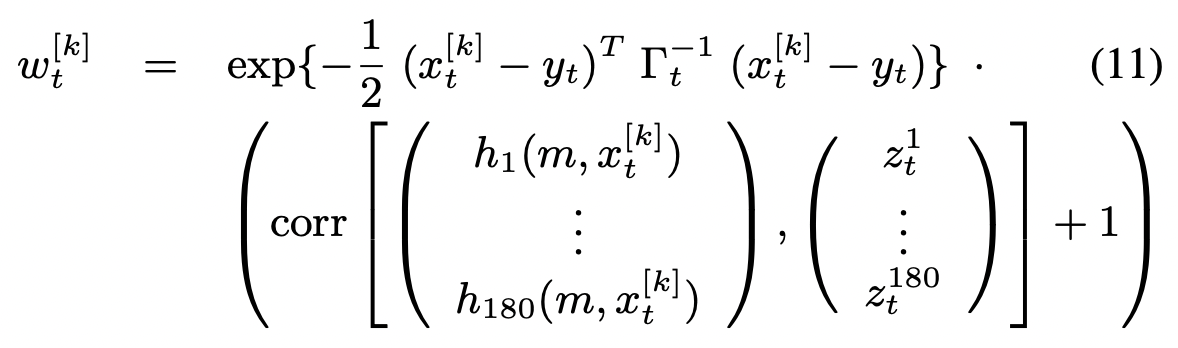
其中corr是Pearson product-moment correlation。实际的重采样以远低于观测/位姿更新的频率进行,以减少variance。以往常一样,重要性权重通过累乘更新。为了避免严重的定位错误,持续地从当前GNSS估计附近采样一小部分粒子。这样可以降低粒子快速远离GPS的风险。
为了消除雨天对路面的影响,对地图和scan做normalization。





