长梅网课-数学P50例2讲解

题面

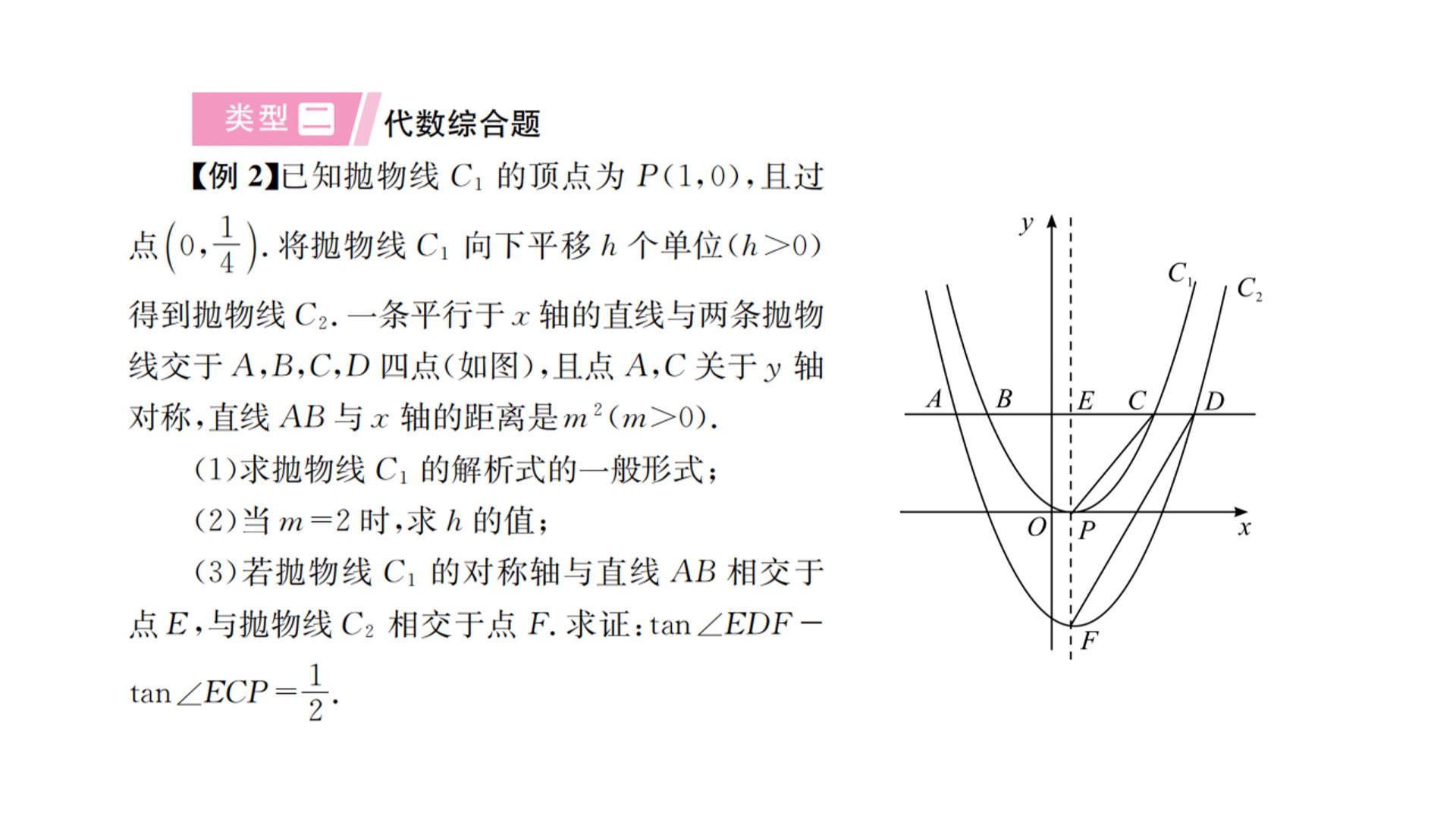
需要说的是书上好像打错了

第一问

我们注意到题目给出了
你要相信出题人绝不会放水他只会放海
于是我们列出顶点式：$y=a(x-1)^2$
然后意外加惊喜地发现还有一个点（0，$\frac{1}{4}$）可用
这不就可以解了吗
$a(0-1)^2=\frac{1}{4}$,解得$a=\frac{1}{4}$
化成一般式为：
$y=\frac{1}{4}x^2-\frac{1}{2}x+\frac{1}{4}$
总结:一个顶点+另一个点=抛物线解析式

第二问

让我们注意一下这句话：

将抛物线$C_1$向下平移$h$个单位得到抛物线$C_2$

得出的结论:$C_2$:$y=\frac{1}{4}(x-1)^2-h$
(向下平移，只有常数项c会改变)
注意这个结论，对理解第三问的法二有帮助
继续讲解
直线$AB$到$x$轴距离为$m^2$
$m=2$,所以距离为$2^2=4$,因此得出点$ABCD$的纵坐标都为4
由于$B$、$C$所处的抛物线$C_1$是已知的，就从$B$、$C$入手
$C_1$:$y=\frac{1}{4}(x-1)^2=4$
$x_1=5$,$x_2=-3$，所以$C(5,4)$
A,C关于$y$轴对称，故$A(-5,4)$
把$A(-5,4)$代入$C_2$,解得h=5
总结:我们可以尝试从已知处多、关联性强的地方进行突破

第三问

气氛突然苏维埃有趣了起来
这种题比较容易让人乍看之下一头雾水满脑糨糊
先分析题目
题目要求证tan∠EDF-tan∠ECP=$\frac{1}{2}$
值得注意的一点：

tan∠A-tan∠B≠tan(∠A-∠B)

不知道有没有人这么做反正不关我事
然后怎么办呢？
看看第二问的总结：我们可以尝试从已知处多、关联性强的地方进行突破
此题没有能一步推出的数据，但不妨碍我们找到能一步推出的关系
于是方法一上场

方法一

从第二问的推导过程中，我们得出：ABCD四个点，知道一个横坐标，就能推出另三个
由于B、C都在$C_1$上，不妨直接用$C_1$解析式中的$x$代入求值
从题目中可推出纵坐标为$m^2$
所以方程为$y=\frac{1}{4}(x-1)^2=m^2$
直接开方即可解得$x_1=1+2m$,$x_2=1-2m$
于是$C(1+2m,m^2)$，又AC关于$y$轴对称，所以$A(-1-2m,m^2)$,AE=ED=2+2m
拿到了点A，代入$C_2$的方程：
$y=\frac{1}{4}(x-1)^2-h$
$=\frac{1}{4}[(-1-2m)-1]^2-h=m^2$
解得h=2m+1 ，所以EF=$h+m^2$=$m^2+2m+1$

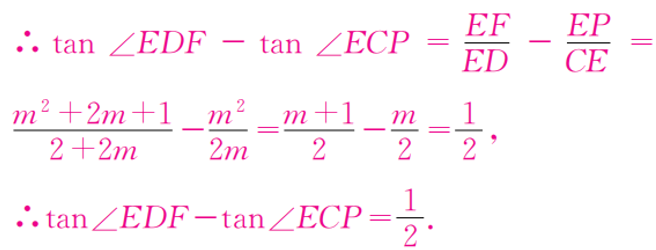
总结:没有数据可推时，可以选择推出未知数间的关系

方法二

先介绍一个引理

引理:二次函数中，△x与△y的关系只由二次项系数a决定

证明:因为图像形状只由二次项系数a决定，老师上课讲过
思维小跳跃预警
设CE为x，则PE=$\frac{1}{4}x^2$(引理，可将PE视作△y)
由对称可得CD=2
得ED=$x+2$
列出方程:
$\frac{1}{4}(x+2)^2-\frac{1}{4}x^2=h$
解释：另行解释
解得h=x+1，即PF=x+1
tan∠EDF-tan∠ECP=$\frac{\frac{1}{4}x^2+(x+1)}{x+2}-\frac{\frac{1}{4}x^2}{x}$=$\frac{1}{2}$
得证
总结:上方引理